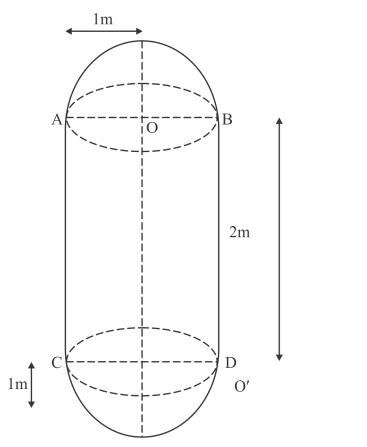
A boiler is in the form of a cylinder 2 m long

Given that:

Height of the cylinder 

Radius of the cylinder and hemisphere are same and is given by

$r=\frac{d}{2}=\frac{2}{2}=1 \mathrm{~m}$

The volume of the cylinder is cylinder is

$V_{1}=\pi r^{2} h$

$=\frac{22}{7} \times 1^{2} \times 2$

$=\frac{22}{7} \times 2 \mathrm{~m}^{3}$

There are two hemispheres at each ends of the cylinder, therefore the volume of the two hemispheres is

$V_{2}=\frac{2}{3} \pi r^{3}+\frac{2}{3} \pi r^{3}$

$=\frac{4}{3} \times \frac{22}{7} \times 1^{3}$

$=\frac{22}{7} \times \frac{4}{3} \mathrm{~m}^{3}$

Therefore, the total volume of the boiler is given by

$V=V_{1}+V_{2}$

$=\left(\frac{22}{7} \times 2+\frac{22}{7} \times \frac{4}{3}\right) \mathrm{m}^{3}$

$=\frac{22}{7} \times \frac{10}{3} \mathrm{~m}^{3}$

$=\frac{220}{21} \mathrm{~m}^{3}$

Hence the volume of the boiler is $V=\frac{220}{21} \mathrm{~m}^{3}$