A boat goes 24 km upstream and 28 km downstream in 6 hrs.

We have to find the speed of the boat in still water and speed of the stream

Let the speed of the boat in still water be x km/hr and the speed of the stream be y km/hr then

Speed upstream $=(x-y) \mathrm{km} / \mathrm{hr}$

Sped down stream $=(x+y) / \mathrm{m} / \mathrm{hr}$

Now, Time taken to cover $28 \mathrm{~km}$ down stream $=\frac{28}{x+y} h r s$

Time taken to cover $24 \mathrm{~km}$ upstream $=\frac{24}{x-y} h r s$

But, total time of journey is 6 hours

$\frac{24}{x-y}+\frac{28}{x+y}=6 \cdots(i)$

Time taken to cover $30 \mathrm{~km}$ upstream $=\frac{30}{x-y} h r s$

Time taken to cover $21 \mathrm{~km}$ down stream $=\frac{21}{x+y} h r s$

In this case total time of journey is given to $6 \frac{1}{2} h r s$ or $\frac{13}{2} h r s$

$\frac{30}{(x-y)}+\frac{21}{(x+y)}=\frac{13}{2}$......(ii)

By $\frac{1}{x-y}=u$ and $\frac{1}{x+y}=v$ in equation (i) and (ii) we get

$24 u+28 v=6$

$30 u+21 v=\frac{13}{2}$

$24 u+28 v-6=0 \cdots($ iii $)$

$30 u+21 v-\frac{13}{2}=0 \cdots(i v)$

Solving these equations by cross multiplication we get

$\frac{u}{28 \times \frac{-13}{2}-21 \times-6}=\frac{-v}{24 \times \frac{-13}{2}-30 \times-6}=\frac{1}{24 \times 21-30 \times 28}$

$\frac{u}{-182+126}=\frac{-v}{-156+180}=\frac{1}{504-840}$

$\frac{u}{-56}=\frac{-v}{24}=\frac{1}{-336}$

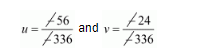
$u=\frac{1}{6}$ and $v=\frac{1}{14}$

Now,

$u=\frac{1}{x-y}=\frac{1}{6}$

$6=x-y \cdots(v)$ and

$v=\frac{1}{14}=\frac{1}{x+y}$

$x+y=14 \cdots(v i)$

By solving equation $(v)$ and $(v i)$ we get,

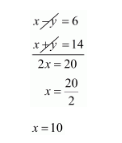
By substituting $x=10$ in equation (vi) we get

Hence, the speed of the stream is $4 \mathrm{~km} / \mathrm{hr}$

The speed of boat is $10 \mathrm{~km} / \mathrm{hr}$