A block of mass m slides on the wooden wedge, which in turn slides backward on the horizontal surface.
A block of mass $m$ slides on the wooden wedge, which in turn slides backward on the horizontal surface. The acceleration of the block with respect to the wedge is: Given $\mathrm{m}=8 \mathrm{~kg}, \mathrm{M}=16 \mathrm{~kg}$
Assume all the surfaces shown in the figure to be frictionless.
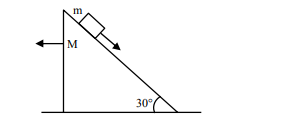
Correct Option: , 4
Let acceleration of wedge is $\mathrm{a}_{1}$ and acceleration of block w.r.t. wedge is $\mathrm{a}_{2}$
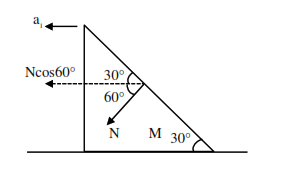
$N \cos 60^{\circ}=M a_{1}=16 a_{1}$
$\Rightarrow \mathrm{N}=32 \mathrm{a}_{1}$
F.B.D. of block w.r.t wedge

$\perp$ to incline
$\mathrm{N}=8 \mathrm{~g} \cos 30^{\circ}-8 \mathrm{a}_{1} \sin 30^{\circ} \Rightarrow 32 \mathrm{a}_{1}=4 \sqrt{3} \mathrm{~g}-4 \mathrm{a}_{1}$
$\Rightarrow \mathrm{a}_{1}=\frac{\sqrt{3}}{9} \mathrm{~g}$
Along incline
$8 g \sin 30^{\circ}+8 \mathrm{a}_{1} \cos 30^{\circ}=\mathrm{ma}_{2}=8 \mathrm{a}_{2}$
$\mathrm{a}_{2}=\mathrm{g} \times \frac{1}{2}+\frac{\sqrt{3}}{9} \mathrm{~g} \cdot \frac{\sqrt{3}}{2}=\frac{2 \mathrm{~g}}{3}$
Option (4)
