A block moving horizontally on a smooth surface with a speed of $40 \mathrm{~ms}^{-1}$ splits into two equal parts. If one of the parts moves at $60 \mathrm{~ms}^{-1}$ in the same direction, then the fractional change in the kinetic energy will be $x: 4$ where $x=$________.
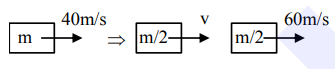
$P_{i}=P_{f}$'
$\mathrm{m} \times 40=\frac{\mathrm{m}}{2} \times \mathrm{v}+\frac{\mathrm{m}}{2} \times 60$
$40=\frac{V}{2}+30$
$\Rightarrow v=20$
$(\mathrm{K} . \mathrm{E} .)_{1}=\frac{1}{2} \mathrm{~m} \times(40)^{2}=800 \mathrm{~m}$
$(\mathrm{K} E .)_{\mathrm{f}}=\frac{1}{2} \frac{\mathrm{m}}{2} \cdot(20)^{2}+\frac{1}{2} \cdot \frac{\mathrm{m}}{2}(60)^{2}=1000 \mathrm{~m}$
$|\Delta \mathrm{K} . \mathrm{E} .|=|1000 \mathrm{~m}-800 \mathrm{~m}|=200 \mathrm{~m}$
$\frac{\Delta \mathrm{K} . \mathrm{E}}{(\mathrm{K} . \mathrm{E} .)_{\mathrm{i}}}=\frac{200 \mathrm{~m}}{800 \mathrm{~m}}=\frac{1}{4}=\frac{\mathrm{x}}{4}$
$|\Delta \mathrm{K} . \mathrm{E}|=|1000 \mathrm{~m}-800 \mathrm{~m}|=200 \mathrm{~m}$
$\frac{\Delta \mathrm{K} \cdot \mathrm{E}}{(\mathrm{K} \cdot \mathrm{E} \cdot)_{i}}=\frac{200 \mathrm{~m}}{800 \mathrm{~m}}=\frac{1}{4}=\frac{\mathrm{x}}{4}$
$x=1$
