A block moving horizontally on a smooth surface with a speed of $40 \mathrm{~m} / \mathrm{s}$ splits into two parts with masses in the ratio of $1: 2$. If the smaller part moves at $60 \mathrm{~m} / \mathrm{s}$ in the same direction, then the fractional change in kinetic energy is :-
Correct Option: , 3
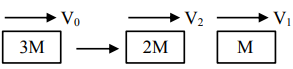
$3 \mathrm{MV}_{0}=2 \mathrm{MV}_{2}+\mathrm{MV}_{1}$
$3 \mathrm{~V}_{0}=2 \mathrm{~V}_{2}+\mathrm{V}_{1}$
$120=2 \mathrm{~V}_{2}+60 \Rightarrow \mathrm{V}_{2}=30 \mathrm{~m} / \mathrm{s}$
$\frac{\Delta \mathrm{K} . \mathrm{E} .}{\mathrm{K} . \mathrm{E} .}=\frac{\frac{1}{2} \mathrm{MV}_{1}^{2}+\frac{1}{2} 2 \mathrm{MV}_{2}^{2}-\frac{1}{2} 3 \mathrm{MV}_{0}^{2}}{\frac{1}{2} 3 \mathrm{MV}_{0}^{2}}$
$=\frac{\mathrm{V}_{1}^{2}+2 \mathrm{~V}_{2}^{2}-3 \mathrm{~V}_{0}^{2}}{3 \mathrm{~V}_{0}^{2}}$
$=\frac{3600+1800-4800}{4800}$
$=\frac{1}{8}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.