A ball of mass $10 \mathrm{~kg}$ moving with a velocity $10 \sqrt{3} \mathrm{~m} / \mathrm{s}$ along the $\mathrm{x}$-axis, hits another ball of mass $20 \mathrm{~kg}$ which is at rest. After the collision, first ball comes to rest while the second ball disintegrates into two equal pieces. One piece starts moving along $y$-axis with a speed of 10 $\mathrm{m} / \mathrm{s}$. The second piece starts moving at an angle of $30^{\circ}$ with respect to the x-axis. The velocity of the ballmoving at $30^{\circ}$ with $x$-axis is $\mathrm{x} \mathrm{m} / \mathrm{s}$. The configuration of pieces after collision is shown in the figure below. The value of $x$ to the nearest integer is________.
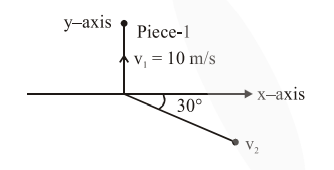
Let velocity of $2^{\text {nd }}$ fragment is $\vec{v}$ then by conservation of linear momentum
$10(10 \sqrt{3}) \hat{\mathrm{i}}=(10)(10 \hat{\mathrm{j}})+10 \overrightarrow{\mathrm{v}}$
$\Rightarrow \overrightarrow{\mathrm{v}}=10 \sqrt{3} \hat{\mathrm{i}}-10 \hat{\mathrm{j}}$
$|\vec{v}|=\sqrt{300+100}=\sqrt{400}=20 \mathrm{~m} / \mathrm{s}$
