$A B C$ and $D B C$ are two triangles on the same base $B C$ such that $A$ and $D$ lie on the opposite sides of $B C, A B=$ $A C$ and $D B=D C$. Show that $A D$ is the perpendicular bisector of $B C$.
Given Two $\triangle A B C$ and $\triangle D B C$ are formed on the same base $B C$ such that $A$ and $D$ lie on the opposite sides of $B C$ such
that $A B=A C$ and $D B=D C$. Also $A D$ intersects $B C$ at $O$. To show $A D$ is the perpendicular bisector of $B C$ i.e., $A D \perp B C$ and
$A D$ bisects $B C$. Proof In $\triangle A B D$ and $\triangle A C D$,
$A B=A C$ [given]
$A D=A D$ [common side]
and BC=D C [given]
$\therefore$ $\triangle A B D \cong \triangle A C D$ [by SSS congruence rule]
$\Rightarrow$ $\angle B A D=\angle C A D$ [by CPCT]
i.e., $\angle B A O=\angle C A O$
In $\triangle A O B$ and $\triangle A O C$,
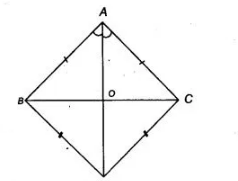

Hence, $A D \perp B C$ and $A D$ bisects $B C$ i.e., $A D$ is the perpendicular bisector of $B C$.
