A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
Thinking Process
- Firstly, inscribe a ΔABC in a circle, then draw the perpendicular bisecters of any two sides of a triangle.
- Secondly, prove that ΔOEA and ΔOEB are congruent by SAS rule and also ΔOMB and ΔOMC are congruent by RHS rule. Further, prove the required result.
Given $A$ circle passing through three points $A, B$ and $C$.
Construction Draw perpendicular bisectors of $A B$ and $A C$ and they meet at a point $O$. Join $O A, O B$ and $O C$.
To prove Perpendicular bisector of $B C$, also passes through $O$ i.e., LO, ON and OM are concurrent.
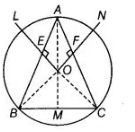
Proof In $\triangle O E A$ and $\triangle O E B$,
$A E=B E$
$[O L$ is the perpendicular bisector of $A B]$
$\angle A E O=\angle B E O$ [each 90°]
and $O E=O E$ [common side]
$\therefore$ $\triangle O E A \equiv O E B$ [by SAS congruence rule]
$\therefore$ $O A=O B$
Similarly, $\Delta O F A \equiv \triangle O F C$ [by SAS congruence rule]
$\begin{array}{llll}\therefore & O A=O C & & \text { [by CPCT] }\end{array}$
$\therefore \quad O A=O B=O C=t \quad$ [say]
Now, we draw a perpendicular from $O$ to the $B C$ and join them. In $\triangle O M B$ and $\triangle O M C$,
$O B=O C$ [proved above]
$O M=O M$ [common side]
and $\quad \angle O M B=\angle O M C \quad$ [each $90^{\circ}$ ]
$\therefore \quad \Delta O M B \equiv \Delta O M C \quad$ [by RHS congruence rule]
$\Rightarrow$ $B M=M C$ [by CPCT]
Hence, $O M$ is the perpendicular bisector of $B C$.
Hence, $O L, O N$ and $O M$ are concurrent.
Hence proved.
