3 + 7 + 14 + 24 + 37 + ...

Solution:

Let $T_{n}$ be the $n$th term and $S_{n}$ be the sum of $n$ terms of the given series.

Thus, we have:

$S_{n}=3+7+14+24+37+\ldots+T_{n-1}+T_{n} \quad \ldots(1)$

Equation (1) can be rewritten as:

$S_{n}=3+7+14+24+37+\ldots+T_{n-1}+T_{n} \quad \ldots$ (2)

On subtracting (2) from (1), we get:

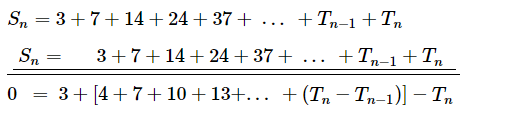
The sequence of difference of successive terms is 4, 7, 10, 13,...

We observe that it is an AP with common difference 3 and first term 4.

Thus, we have:

$3+\left[\frac{(n-1)}{2}\{8+(n-2) 3\}\right]-T_{n}=0$

$\Rightarrow 3+\left[\frac{(n-1)}{2}(3 n+2)\right]-T_{n}=0$

$\Rightarrow\left[\frac{3 n^{2}-n+4}{2}\right]=T_{n}$

$\Rightarrow\left[\frac{3}{2} n^{2}-\frac{n}{2}+2\right]=T_{n}$

Now,

$\because S_{n}=\sum_{k=1}^{n} T_{k}$

$\therefore S_{n}=\sum_{k=1}^{n}\left(\frac{3}{2} k^{2}-\frac{k}{2}+2\right)$

$\Rightarrow S_{n}=\frac{3}{2} \sum_{k=1}^{n} k^{2}+\sum_{k=1}^{n} 2-\frac{1}{2} \sum_{k=1}^{n} k$

$\Rightarrow S_{n}=\frac{n(n+1)(2 n+1)}{4}+2 n-\frac{n(n+1)}{4}$

$\Rightarrow S_{n}=\frac{n(n+1)(2 n)+8 n}{4}$

$\Rightarrow S_{n}=\frac{(n+1)\left(2 n^{2}\right)+8 n}{4}$

$\Rightarrow S_{n}=\frac{n}{2}[n(n+1)+4]$

$\Rightarrow S_{n}=\frac{n}{2}\left[n^{2}+n+4\right]$