2 women and 5 men can together finish a piece of embroidery in 4 days,

1 women alone can finish the work in $x$ days and 1 man alone can finish it in $y$ days then

One woman one day work $=\frac{1}{x}$

One man one days work $=\frac{1}{y}$

2 women's one days work $=\frac{2}{x}$

5 man's one days work $=\frac{5}{y}$

Since 2 women and 5 men can finish the work in 4 days

$4\left(\frac{2}{x}+\frac{5}{y}\right)=1$

$\frac{8}{x}+\frac{20}{y}=1 \cdots(i)$

3 women and 6 men can finish the work in 3 days

$3\left(\frac{3}{x}+\frac{6}{y}\right)=1$

$\frac{9}{x}+\frac{18}{y}=1 \cdots(i i)$

Putting $\frac{1}{x}=u$ and $\frac{1}{y}=v$ in equation $(i)$ and $(i i)$ we get

$8 u+20 v-1=0 \cdots(i i i)$

$9 u+18 v-1=0 \cdots(i v)$

By using cross multiplication we have

$\frac{u}{(20 \times-1)-(18 \times-1)}=\frac{-v}{(8 \times-1)-(9 \times-1)}=\frac{1}{(8 \times 18)-(9 \times 20)}$

$\frac{u}{-20+18}=\frac{-v}{-8+9}=\frac{1}{144-180}$

$\frac{u}{-2}=\frac{-v}{1}=\frac{1}{-36}$

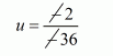
$u=\frac{1}{18}$

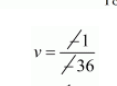
$v=\frac{1}{36}$

Now ,

$u=\frac{1}{18}$

$\frac{1}{x}=\frac{1}{18}$

$x=18$

$v=\frac{1}{60}$

$\frac{1}{y}=\frac{1}{60}$

$y=60$

Hence, the time taken by 1 woman alone to finish the embroidery is 36 days,

The time taken by 1 man alone to finish the embroidery is 18 days.