100 surnames were randomly picked up from a local telephone directly and the frequency

Consider the following table.

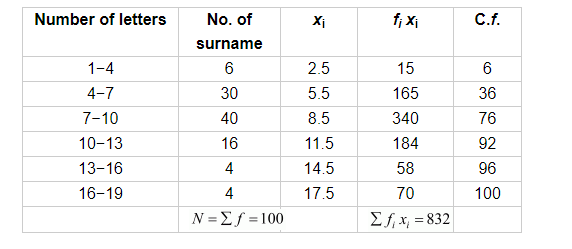
Here, the maximum frequency is 40 so the modal class is 7−10.

Therefore,

$l=7$

$h=3$

$f=40$

$f_{1}=30$

$f_{2}=16$

$\Rightarrow$ Mode $=l+\frac{f-f_{1}}{2 f-f_{1}-f_{2}} \times h$

$=7+\frac{10}{34} \times 3$

$=7+\frac{30}{34}$

Mode $=7.88$

Thus, the modal sizes of the surnames is 7.88.

Mean $=\frac{\sum f_{i} x_{i}}{\sum f}$

$=\frac{832}{100}$

Mean $=8.32$

Thus, the mean number of letters in the surnames is 8.32.

Median

$=l+\frac{\frac{N}{2}-F}{f} \times h$

$=7+\frac{50-36}{40} \times 3$

$=7+\frac{21}{20}$

Median $=8.05$

Thus, the median number of letters in the surnames is 8.05.