
Hey, are you a class 11 student and looking for ways to download NCERT Solutions for Class 11 Physics chapter 13 "Kinetic Theory"? If yes. Then read this post till the end.
In this article, we have listed NCERT solution for class 11 Physics Chapter 13 in PDF that are prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to learn and understand class 11 Physics chapter 13 "Kinetic Theory" in an easy way then you can use these solutions PDF.
NCERT Solutions helps students to Practice important concepts of subjects easily. Class 11 Physics solutions provide detailed explanations of all the NCERT questions that students can use to clear their doubts instantly.
If you want to score high in your class 11 Physics Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.
In this article, we have listed NCERT Solution for Class 11 Physics chapter 13 that you can download to start your preparations anytime.
So, without wasting more time Let’s start.
Question.1: Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3Å.
Solution. Diameter of an oxygen molecule, $d=3$
Radius, $r=\frac{d}{2}=\frac{3}{2}=1.5 \mathrm{~A}=1.5 \times 10^{-8} \mathrm{~cm}$
Actual volume occupied by 1 mole of oxygen gas at $\mathrm{STP}=22400 \mathrm{~cm}^{3}$
Molecular volume of oxygen gas, $V=\frac{4}{3} \pi r^{3} \cdot N$
Where, $N$ is Avogadro's number $=6.023 \times 10^{23}$ molecules/mole
$\therefore V=\frac{4}{3} \times 3.14 \times\left(1.5 \times 10^{-8}\right)^{3} \times 6.023 \times 10^{23}=8.51 \mathrm{~cm}^{3}$
Ratio of the molecular volume to the actual volume of oxygen $=\frac{8.51}{22400}$ $=3.8 \times 10^{-4}$
Question.2 :Molar volume is the volume occupied by 1 mol of any (ideal) gas at standard temperature and pressure (STP: 1 atmospheric pressure, $0^{\circ} \mathrm{C}$ ). Show that it is $22.4$ liters.
Solution. The ideal gas equation relating pressure $(P)$, volume $(V)$, and absolute temperature $(T)$ is given as:
$P V=n R T$
Where,
$R$ is the universal gas constant $=8.314 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$
$n=$ Number of moles $=1$
$T=$ Standard temperature $=273 \mathrm{~K}$
$P=$ Standard pressure $=1 \mathrm{~atm}=1.013 \times 10^{5} \mathrm{Nm}^{-2}$
$\therefore V=\frac{n R T}{P}$
$=\frac{1 \times 8.314 \times 273}{1.013 \times 10^{5}}$
$=22.4$ litres
$=\frac{1 \times 8.314 \times 273}{1.013 \times 10^{5}}$
$=0.0224 \mathrm{~m}^{3}$
$=22.4$ litres
Hence, the molar volume of a gas at STP is $22.4$ litres.
Question.3: Figure $13.8$ shows plot of $P V I T$ versus Pfor $1.00 \times 10^{-3} \mathrm{~kg}$ of oxygen gas at two different temperatures.
Solution.
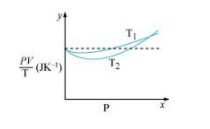
(a) What does the dotted plot signify?
(b) Which is true: $T_{1}>T_{2}$ or $T_{1}
(d) If we obtained similar plots for $1.00 \times 10^{-3} \mathrm{~kg}$ of hydrogen, would we get the same value of $P V I T$ at the point where the curves meet on the $y$ -axis? If not, what mass of hydrogen yields the same value of $P V I T$ (for low pressure high temperature region of the plot)? (Molecular mass of $\mathrm{H}_{2}=2.02 \mathrm{u}$, of $\mathrm{O}_{2}=32.0 \mathrm{u}, R=8.31 \mathrm{~J} \mathrm{mo} 1^{-1} \mathrm{~K}^{-1}$.)
Solution. (a) The dotted plot in the graph signifies the ideal behaviour of the gas, i.e., the ratio $\frac{P V}{T}$ is equal. $\mu R$ ( $\mu$ is the number of moles and $R$ is the universal gas constant) is a constant quality. It is not dependent on the pressure of the gas
(b) The dotted plot in the given graph represents an ideal gas. The curve of the gas at temperature $T_{1}$ is closer to the dotted plot than the curve of the gas at temperature $T_{2}$. A real gas approaches the behaviour of an ideal gas when its temperature increases. Therefore, $T_{1}>T_{2}$ is true for the given plot.
(c) The value of the ratio $P V I T$, where the two curves meet, is $\mu R$. This is because the ideal gas equation is given as:
$P V=\mu R T$
$\frac{P V}{T}=\mu R$
Where,
$P$ is the pressure
$T$ is the temperature
$V$ is the volume
$\mu$ is the number of moles
$R$ is the universal constant
Molecular mass of oxygen $=32.0 \mathrm{~g}$
Mass of oxygen $=1 \times 10^{-3} \mathrm{~kg}=1 \mathrm{~g}$
$R=8.314 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}$
$\therefore \frac{P V}{T}=\frac{1}{32} \times 8.314$
$=0.26 \mathrm{~J} \mathrm{~K}^{-1}$
Therefore, the value of the ratio $P V / T$, where the curves meet on the $y$ -axis, is
$0.26 \mathrm{~J} \mathrm{~K}^{-1}$
(d) If we obtain similar plots for $1.00 \times 10^{-3} \mathrm{~kg}$ of hydrogen, then we will not get the same value of $P V / T$ at the point where the curves meet the $y$ -axis. This is because the molecular mass of hydrogen $(2.02 \mathrm{u})$ is different from that of oxygen $(32.0 \mathrm{u})$.
We have:
$\frac{P V}{T}=0.26 \mathrm{~J} \mathrm{~K}^{-1}$
$R=8.314 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}$
Molecular mass $(M)$ of $\mathrm{H}_{2}=2.02 \mathrm{u}$
$\frac{P V}{T}=\mu R$ at constant temperature
Where, $\mu=\frac{m}{M}$
$m=$ Mass of $\mathrm{H}_{2}$
$\therefore m=\frac{P V}{T} \times \frac{M}{R}$
$=\frac{0.26 \times 2.02}{8.31}$
$=6.3 \times 10^{-2} \mathrm{~g}=6.3 \times 10^{-5} \mathrm{~kg}$
Hence, $6.3 \times 10^{-5} \mathrm{~kg}$ of $\mathrm{H}_{2}$ will yield the same value of $P V / T$.
Question.4: An oxygen cylinder of volume 30 litres has an initial gauge pressure of $15 \mathrm{~atm}$ and a temperature of $27^{\circ} \mathrm{C}$. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to $11 \mathrm{~atm}$ and its temperature drops to $17^{\circ} \mathrm{C}$. Estimate the mass of oxygen taken out of the cylinder $\left(R=8.31 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}\right.$, molecular mass of $\mathrm{O}_{2}=32 \mathrm{u}$ ).
Solution. Volume of oxygen, $V_{1}=30$ litres $=30 \times 10^{-3} \mathrm{~m}^{3}$
Gauge pressure, $P_{1}=15 \mathrm{~atm}=15 \times 1.013 \times 10^{5} \mathrm{~Pa}$
Temperature, $T_{1}=27^{\circ} \mathrm{C}=300 \mathrm{~K}$
Universal gas constant, $R=8.314 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}$
Let the initial number of moles of oxygen gas in the cylinder be $n_{1}$.
The gas equation is given as:
$P_{1} V_{1}=n_{1} R T_{1}$
$\therefore n_{1}=\frac{P_{1} V_{1}}{R T_{1}}$
$=\frac{15.195 \times 10^{5} \times 30 \times 10^{-3}}{(8.314) \times 300}=18.276$
But, $n_{1}=\frac{m_{1}}{M}$
Where,
$m_{1}=$ Initial mass of oxygen
$M=$ Molecular mass of oxygen $=32 \mathrm{~g}$
$\therefore m_{1}=n_{1} M=18.276 \times 32=584.84 \mathrm{~g}$
After some oxygen is withdrawn from the cylinder, the pressure and temperature reduces.
Volume, $V_{2}=30$ litres $=30 \times 10^{-3} \mathrm{~m}^{3}$
Gauge pressure, $P_{2}=11 \mathrm{~atm}=11 \times 1.013 \times 10^{5} \mathrm{~Pa}$
Temperature, $T_{2}=17^{\circ} \mathrm{C}=290 \mathrm{~K}$
Let $n_{2}$ be the number of moles of oxygen left in the cylinder.
The gas equation is given as:
$P_{2} V_{2}=n_{2} R T_{2}$
$\therefore n_{2}=\frac{P_{2} V_{2}}{R T_{2}}$
$=\frac{11.143 \times 10^{5} \times 30 \times 10^{-3}}{8.314 \times 290}=13.86$
But, $n_{2}=\frac{m_{2}}{M}$
Where,
$m_{2}$ is the mass of oxygen remaining in the cylinder
$\therefore m_{2}=n_{2} M=13.86 \times 32=453.1 \mathrm{~g}$
The mass of oxygen taken out of the cylinder is given by the relation:
Initial mass of oxygen in the cylinder $-$ Final mass of oxygen in the cylinder
$=m_{1}-m_{2}$
$=584.84 \mathrm{~g}-453.1 \mathrm{~g}$
$=131.74 \mathrm{~g}$
$=0.131 \mathrm{~kg}$
Therefore, $0.131 \mathrm{~kg}$ of oxygen is taken out of the cylinder.
Question. 5: An air bubble of volume $1.0 \mathrm{~cm}^{3}$ rises from the bottom of a lake $40 \mathrm{~m}$ deep at a temperature of $12^{\circ} \mathrm{C}$. To what volume does it grow when it reaches the surface, which is at a temperature of $35^{\circ} \mathrm{C} ?$
Solution. Volume of the air bubble, $V_{1}=1.0 \mathrm{~cm}^{3}=1.0 \times 10^{-6} \mathrm{~m}^{3}$
Bubble rises to height, $d=40 \mathrm{~m}$
Temperature at a depth of $40 \mathrm{~m}, T_{1}=12^{\circ} \mathrm{C}=285 \mathrm{~K}$
Temperature at the surface of the lake, $T_{2}=35^{\circ} \mathrm{C}=308 \mathrm{~K}$
The pressure on the surface of the lake:
$P_{2}=1 \mathrm{~atm}=1 \times 1.013 \times 10^{5} \mathrm{~Pa}$
The pressure at the depth of $40 \mathrm{~m}$ :
$P_{1}=1 \mathrm{~atm}+\mathrm{dog}$
Where,
$\rho$ is the density of water $=10^{3} \mathrm{~kg} / \mathrm{m}^{3}$
$\mathrm{g}$ is the acceleration due to gravity $=9.8 \mathrm{~m} / \mathrm{s}^{2}$
$\therefore P_{1}=1.013 \times 10^{5}+40 \times 10^{3} \times 9.8=493300 \mathrm{~Pa}$
We have: $\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}$
Where, $V_{2}$ is the volume of the air bubble when it reaches the surface
$V_{2}=\frac{P_{1} V_{1} T_{2}}{T_{1} P_{2}}$
Therefore, when the air bubble reaches the surface, its volume becomes $5.263 \mathrm{~cm}^{3}$.
Question.6: Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity $25.0 \mathrm{~m}^{3}$ at a temperature of $27^{\circ} \mathrm{C}$ and 1 atm pressure.
Solution. Volume of the room, $V=25.0 \mathrm{~m}^{3}$
Temperature of the room, $T=27^{\circ} \mathrm{C}=300 \mathrm{~K}$
Pressure in the room, $P=1 \mathrm{~atm}=1 \times 1.013 \times 10^{5} \mathrm{~Pa}$
The ideal gas equation relating pressure $(P)$, Volume $(V)$, and absolute temperature ( $T$ ) can be written as:
$P V=K_{B} N T$
Where,
$K_{B}$ is Boltzmann constant $=1.38 \times 10^{-23} \mathrm{~m}^{2} \mathrm{~kg} \mathrm{~s}^{-2} \mathrm{~K}^{-1}$
$N$ is the number of air molecules in the room $\therefore N=\frac{P V}{k_{B} T}$
$=\frac{1.013 \times 10^{5} \times 25}{1.38 \times 10^{-23} \times 300}=6.11 \times 10^{26}$ molecules
Therefore, the total number of air molecules in the given room is $6.11 \times 10^{26}$.
Question.7:Estimate the average thermal energy of a helium atom at (i) room temperature $\left(27^{\circ} \mathrm{C}\right)$, (ii) the temperature on the surface of the Sun $(6000 \mathrm{~K})$, (iii) the temperature of 10 million Kelvin (the typical core temperature in the case of a star).
Solution. (i) At room temperature, $T=27^{\circ} \mathrm{C}=300 \mathrm{~K}$
Average thermal energy $=\frac{3}{2} k T$
Where $k$ is Boltzmann constant $=1.38 \times 10^{-23} \mathrm{~J} \mathrm{~K}^{-1}$
$\therefore \frac{3}{2} k T=\frac{3}{2} \times 1.38 \times 10^{-23} \times 300 \mathrm{~J}$
$=6.21 \times 10^{-21} \mathrm{~J}$
Hence, the average thermal energy of a helium atom at room temperature $\left(27^{\circ} \mathrm{C}\right)$ is $6.21 \times 10^{-21} \mathrm{~J}$.
(ii) On the surface of the sun, $T=6000 \mathrm{~K}$ Average thermal energy $=\frac{3}{2} k T$
$=\frac{3}{2} k T=\frac{3}{2} \times 1.38 \times 10^{-23} \times 6000 \mathrm{~J}$
$=1.241 \times 10^{-19} \mathrm{~J}$ Hence, the average thermal energy of a helium atom on the surface of the sun is $1.241 \times 10^{-18} \mathrm{~J}$.
(iii) At temperature, $T=10^{7} \mathrm{~K}$
Average thermal energy $=\frac{3}{2} k T$
$=\frac{3}{2} \times 1.38 \times 10^{-23} \times 10^{7} \mathrm{~J}$
$=2.07 \times 10^{-16} \mathrm{~J}$
Hence, the average thermal energy of a helium atom at the core of a star is $2.07 \times 10^{-16} \mathrm{~J}$.
Question .8: Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contain equal number of respective molecules? Is the root mean square speed of molecules the same in the three cases? If not, in which case is $v_{r m s}$ the largest?
Solution. Yes. All contain the same number of the respective molecules.
No. The root mean square speed of neon is the largest.
Since the three vessels have the same capacity, they have the same volume.
Hence, each gas has the same pressure, volume, and temperature.
According to Avogadro's law, the three vessels will contain an equal number of the respective molecules. This number is equal to Avogadro's number, $N=6.023 \times 10^{23}$.
The root mean square speed $\left(v_{r m s}\right)$ of a gas of mass $m$, and temperature $T$, is given by the relation:
$v_{\mathrm{rms}}=\sqrt{\frac{3 k T}{m}}$
Where, $k$ is Boltzmann constant
For the given gases, $k$ and $T$ are constants.
Hence $v_{\text {rms }}$ depends only on the mass of the atoms, i.e.,
$v_{\mathrm{ms}} \propto \sqrt{\frac{1}{m}}$
Therefore, the root mean square speed of the molecules in the three cases is not the same. Among neon, chlorine, and uranium hexafluoride, the mass of neon is the smallest. Hence, neon has the largest root mean square speed among the given gases.
Question.9:At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at $-20^{\circ} \mathrm{C} ?$ (atomic mass of $\mathrm{Ar}=39.9 \mathrm{u}$, of $\mathrm{He}=4.0 \mathrm{u}$ ).
Solution. Temperature of the helium atom, $T_{\mathrm{He}}=-20^{\circ} \mathrm{C}=253 \mathrm{~K}$
Atomic mass of argon, $M_{\mathrm{Ar}}=39.9 \mathrm{u}$
Atomic mass of helium, $M_{\mathrm{He}}=4.0 \mathrm{u}$
Let, $\left(V_{r m s}\right)_{A r}$ be the rms speed of argon.
Let $\left(V_{\text {rms }}\right)_{\mathrm{He}}$ be the rms speed of helium.
The rms speed of argon is given by:
$\left(v_{r m s}\right)_{A r}=\sqrt{\frac{3 R T_{A r}}{M_{A r}}} \ldots(i)$
Where,
$R$ is the universal gas constant
$T_{\mathrm{Ar}}$ is temperature of argon gas
The rms speed of helium is given by:
$\left(v_{\mathrm{mos}}\right)_{\mathrm{He}}=\sqrt{\frac{3 R T_{\mathrm{He}}}{M_{\mathrm{He}}}} \ldots$ (ii)
It is given that:
$\left(V_{\mathrm{rms}}\right)_{\mathrm{Ar}}=\left(V_{\mathrm{rms}}\right)_{\mathrm{He}}$
$\sqrt{\frac{3 R T_{\mathrm{Ar}}}{M_{\mathrm{Ar}}}}=\sqrt{\frac{3 R T_{\mathrm{He}}}{M_{\mathrm{He}}}}$
$\frac{T_{\mathrm{Ar}}}{M_{\mathrm{Ar}}}=\frac{T_{\mathrm{He}}}{M_{\mathrm{H}_{e}}}$
$T_{\mathrm{At}}=\frac{T_{\mathrm{HC}}}{M_{\mathrm{Hc}}} \times M_{\mathrm{Ar}}$
$=\frac{253}{4} \times 39.9$
$=2523.675=2.52 \times 10^{3} \mathrm{~K}$
Therefore, the temperature of the argon atom is $2.52 \times 10^{3} \mathrm{~K}$.
Question.10: Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at $2.0 \mathrm{~atm}$ and temperature $17^{\circ} \mathrm{C}$. Take the radius of a nitrogen molecule to be roughly $1.0$ Á. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of $\mathrm{N}_{2}=28.0 \mathrm{u}$ ).
Solution. Mean free path $=1.11 \times 10^{-7} \mathrm{~m}$
Collision frequency $=4.58 \times 10^{9} \mathrm{~s}^{-1}$
Successive collision time $\approx 500 \times$ (Collision time)
Pressure inside the cylinder containing nitrogen, $P=2.0 \mathrm{~atm}=2.026 \times 10^{5} \mathrm{~Pa}$
Temperature inside the cylinder, $T=17^{\circ} \mathrm{C}=290 \mathrm{~K}$
Radius of a nitrogen molecule, $r=1.0 \mathrm{~A}=1 \times 10^{10} \mathrm{~m}$
Diameter, $d=2 \times 1 \times 10^{10}=2 \times 10^{10} \mathrm{~m}$
Molecular mass of nitrogen, $M=28.0 \mathrm{~g}=28 \times 10^{-3} \mathrm{~kg}$
The root mean square speed of nitrogen is given by the relation:
$v_{\mathrm{rms}}=\sqrt{\frac{3 R T}{M}}$
Where,
$R$ is the universal gas constant $=8.314 \mathrm{~J}$ mole $^{-1} \mathrm{~K}^{-1}$
$\therefore v_{\mathrm{ms}}=\sqrt{\frac{3 \times 8.314 \times 290}{28 \times 10^{-3}}}=508.26 \mathrm{~m} / \mathrm{s}$
The mean free path ( $I$ ) is given by the relation:
$I=\frac{k T}{\sqrt{2} \times d^{2} \times P}$
Where,
$k$ is the Boltzmann constant $=1.38 \times 10^{-23} \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-2} \mathrm{~K}^{-1}$
$\therefore I=\frac{1.38 \times 10^{-23} \times 290}{\sqrt{2} \times 3.14 \times\left(2 \times 10^{-10}\right)^{2} \times 2.026 \times 10^{5}}$
$=1.11 \times 10^{-7} \mathrm{~m}$
Collision frequency $=\frac{v_{r m s}}{l}$
$=\frac{508.26}{1.11 \times 10^{-7}}=4.58 \times 10^{9} \mathrm{~s}^{-1}$
Collision time is given as:
$T=\frac{d}{v_{\mathrm{rms}}}$
$=\frac{2 \times 10^{-10}}{508.26}=3.93 \times 10^{-13} \mathrm{~S}$
Time taken between successive collisions:
$T^{\prime}=\frac{l}{v_{\mathrm{rms}}}$
$=\frac{1.11 \times 10^{-7} \mathrm{~m}}{508.26 \mathrm{~m} / \mathrm{s}}=2.18 \times 10^{-10} \mathrm{~s}$
$\therefore \frac{T^{\prime}}{T}=\frac{2.18 \times 10^{-10}}{3.93 \times 10^{-13}}=500$
Hence, the time taken between successive collisions is 500 times the time taken for a collision.
Question.11:A metre long narrow bore held horizontally (and closed at one end) contains a $76 \mathrm{~cm}$ long mercury thread, which traps a $15 \mathrm{~cm}$ column of air. What happens if the tube is held vertically with the open end at the bottom?
Solution. Length of the narrow bore, $L=1 \mathrm{~m}=100 \mathrm{~cm}$
Length of the mercury thread, $/=76 \mathrm{~cm}$
Length of the air column between mercury and the closed end, $l_{a}=15 \mathrm{~cm}$
Since the bore is held vertically in air with the open end at the bottom, the mercury length that occupies the air space is: $100-(76+15)=9 \mathrm{~cm}$
Hence, the total length of the air column $=15+9=24 \mathrm{~cm}$
Let $h \mathrm{~cm}$ of mercury flow out as a result of atmospheric pressure.
$\therefore$ Length of the air column in the bore $=24+h \mathrm{~cm}$
And, length of the mercury column $=76-h \mathrm{~cm}$
Initial pressure, $P_{1}=76 \mathrm{~cm}$ of mercury
Initial volume, $V_{1}=15 \mathrm{~cm}^{3}$
Final pressure, $P_{2}=76-(76-h)=h \mathrm{~cm}$ of mercury
Final volume, $V_{2}=(24+h) \mathrm{cm}^{3}$
Temperature remains constant throughout the process.
$\therefore P_{1} V_{1}=P_{2} V_{2}$
$76 \times 15=h(24+h)$
$h^{2}+24 h-1140=0$
$\therefore h=\frac{-24 \pm \sqrt{(24)^{2}+4 \times 1 \times 1140}}{2 \times 1}$
$=23.8 \mathrm{~cm}$ or $-47.8 \mathrm{~cm}$
Height cannot be negative. Hence, $23.8 \mathrm{~cm}$ of mercury will flow out from the bore and $52.2 \mathrm{~cm}$ of mercury will remain in it. The length of the air column will be $24+23.8=47.8 \mathrm{~cm}$.
Question.12: From a certain apparatus, the diffusion rate of hydrogen has an average value of $28.7 \mathrm{~cm}^{3} \mathrm{~s}^{-1}$. The diffusion of another gas under the same conditions is measured to have an average rate of $7.2 \mathrm{~cm}^{3}$ $\mathrm{s}^{-1}$. Identify the gas.
[Hint: Use Graham's law of diffusion: $\mathrm{R}_{1} / \mathrm{R}_{2}=\left(\mathrm{M}_{2} / \mathrm{M}_{1}\right)^{1 / 2}$, where $\mathrm{R}_{1}, \mathrm{R}_{2}$ are diffusion rates of gases 1 and 2, and $\mathrm{M}_{1}$ and $\mathrm{M}_{2}$ their respective molecular masses. The law is a simple consequence of kinetic theory.]
Solution. Rate of diffusion of hydrogen, $R_{1}=28.7 \mathrm{~cm}^{3} \mathrm{~s}^{-1}$
Rate of diffusion of another gas, $R_{2}=7.2 \mathrm{~cm}^{3} \mathrm{~s}^{-1}$
According to Graham's Law of diffusion, we have:
$\frac{R_{1}}{R_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}$
$=2.02\left(\frac{28.7}{7.2}\right)^{2}=32.09 \mathrm{~g}$
$32 \mathrm{~g}$ is the molecular mass of oxygen. Hence, the unknown gas is oxygen.
Question.13 A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so-called law of atmospheres
$n_{2}=n_{1} \exp \left[-m g\left(h_{2}-h_{1}\right) / k_{B} T\right]$
Where $n_{2}, n_{1}$ refer to number density at heights $h_{2}$ and $h_{1}$ respectively. Use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid column:
$n_{2}=n_{1} \exp \left[-m g N_{A}\left(\rho-P^{\prime}\right)\left(h_{2}-h_{1}\right) /(\rho R T)\right]$
Where $\rho$ is the density of the suspended particle, and $\rho$ ' that of surrounding medium. $\left[N_{A}\right.$ is Avogadro's number, and $R$ the universal gas constant.] [Hint: Use Archimedes principle to find the apparentweight of the suspended particle.]
Solution. According to the law of atmospheres, we have:
$n_{2}=n_{1} \exp \left[-m g\left(h_{2}-h_{1}\right) / k B T\right] \ldots(i)$
Where,
$n_{1}$ is thenumber density at height $h_{1}$, and $n_{2}$ is the number density at height $h_{2}$
$m g$ is the weight of the particle suspended in the gas column
Density of the medium $=\rho^{\prime}$
Density of the suspended particle $=\rho$
Mass of one suspended particle $=m^{\prime}$
Mass of the medium displaced $=m$
Volume of a suspended particle $=V$
According to Archimedes' principle for a particle suspended in a liquid column, the effective weight of the suspended particle is given as:
Weight of the medium displaced - Weight of the suspended particle
$=m g-m^{\prime} g$
$=m g-V \rho^{\prime} g=m g-\left(\frac{m}{\rho}\right) \rho^{\prime} g$
$=m g\left(1-\frac{\rho^{\prime}}{\rho}\right) \quad \ldots(i i)$
Gas constant, $R=k_{B} N$
$k_{s}=\frac{R}{N} \ldots$ (iii)
Substituting equation (ii) in place of $m g$ in equation $(i)$ and then using equation (iii), we get:
$n_{2}=n_{1} \exp \left[-m g\left(h_{2}-h_{1}\right) / k_{B} T\right]$
$=n_{1} \exp \left[-m g\left(1-\frac{\rho^{\prime}}{\rho}\right)\left(h_{2}-h_{1}\right) \frac{N}{R T}\right]$
$=n_{1} \exp \left[-m g\left(\rho-\rho^{\prime}\right)\left(h_{2}-h_{1}\right) \frac{N}{R T \rho}\right]$
Question.14: Given below are densities of some solids and liquids. Give rough estimates of the size of their atoms:
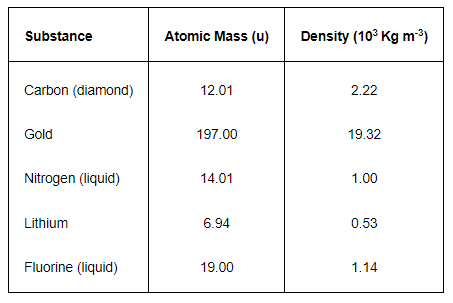
[Hint: Assume the atoms to be 'tightly packed' in a solid or liquid phase, and use the known value of Avogadro's number. You should, however, not take the actual numbers you obtain for various atomic sizes too literally. Because of the crudeness of the tight packing approximation, the results only indicate that atomic sizes are in the range of a few $$.
Solution.
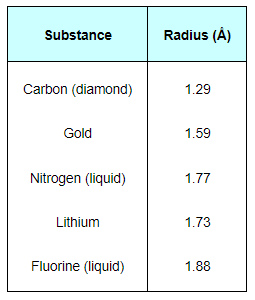
Atomic mass of a substance $=M$
Density of the substance $=\rho$
Avogadro's number $=N=6.023 \times 10^{23}$
Volume of each atom $=\frac{4}{3} \pi r^{3}$
Volume of $N$ number of molecules $=\frac{4}{3} \pi r^{3} N \ldots(i)$
Volume of one mole of a substance $=\frac{M}{\rho} \ldots$ (ii)
$\frac{4}{3} \pi r^{3} N=\frac{M}{\rho}$
$\therefore r=\sqrt[3]{\frac{3 M}{4 \pi \rho N}}$
For carbon:
$M=12.01 \times 10^{-3} \mathrm{~kg}$,
$\rho=2.22 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 12.01 \times 10^{-3}}{4 \pi \times 2.22 \times 10^{3} \times 6.023 \times 10^{23}}\right)^{\frac{1}{3}}=1.29 \mathrm{~A}$
Hence, the radius of a carbon atom is $1.29$.
For gold:
$M=197.00 \times 10^{-3} \mathrm{~kg}$
$\rho=19.32 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 197 \times 10^{-3}}{4 \pi \times 19.32 \times 10^{3} \times 6.023 \times 10^{23}}\right)^{\frac{1}{3}}=1.59 \AA{A}$
Hence, the radius of a gold atom is $1.59$.
For liquid nitrogen:
$M=14.01 \times 10^{-3} \mathrm{~kg}$
$\rho=1.00 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 14.01 \times 10^{-3}}{4 \pi \times 1.00 \times 10^{3} \times 6.23 \times 10^{23}}\right)^{\frac{1}{3}}=1.77 \AA$
Hence, the radius of a liquid nitrogen atom is $1.77 \AA$.
For lithium:
$M=6.94 \times 10^{-3} \mathrm{~kg}$
$\rho=0.53 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 6.94 \times 10^{-3}}{4 \pi \times 0.53 \times 10^{3} \times 6.23 \times 10^{23}}\right)^{\frac{1}{3}}=1.73 \mathrm{~A}$
Hence, the radius of a lithium atom is $1.73 \AA{A}$.
For liquid fluorine:
$M=19.00 \times 10^{-3} \mathrm{~kg}$
$\rho=1.14 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 19 \times 10^{-3}}{4 \pi \times 1.14 \times 10^{3} \times 6.023 \times 10^{23}}\right)^{\frac{1}{3}}=1.88 \AA$
Hence, the radius of a liquid fluorine atom is $1.88 \mathrm{~A}$.
So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.
Also Read,
Download Class 11 Physics Notes Free PDF
Download Class 11 Physics Book Chapterwise Free PDF
Download Class 11 Physics Exemplar Chapterwise Free PDF
If you have any Confusion related to NCERT Solutions for Class 11 Physics chapter 13 then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 11 Physics by Kota’s top IITian’s Faculties Install the eSaral App
In this article, we have listed NCERT solution for class 11 Physics Chapter 13 in PDF that are prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to learn and understand class 11 Physics chapter 13 "Kinetic Theory" in an easy way then you can use these solutions PDF.
NCERT Solutions helps students to Practice important concepts of subjects easily. Class 11 Physics solutions provide detailed explanations of all the NCERT questions that students can use to clear their doubts instantly.
If you want to score high in your class 11 Physics Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.
In this article, we have listed NCERT Solution for Class 11 Physics chapter 13 that you can download to start your preparations anytime.
So, without wasting more time Let’s start.
Download The PDF of NCERT Solutions for Class 11 Physics Chapter 13 "Kinetic Theory"
Question.1: Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3Å.
Solution. Diameter of an oxygen molecule, $d=3$
Radius, $r=\frac{d}{2}=\frac{3}{2}=1.5 \mathrm{~A}=1.5 \times 10^{-8} \mathrm{~cm}$
Actual volume occupied by 1 mole of oxygen gas at $\mathrm{STP}=22400 \mathrm{~cm}^{3}$
Molecular volume of oxygen gas, $V=\frac{4}{3} \pi r^{3} \cdot N$
Where, $N$ is Avogadro's number $=6.023 \times 10^{23}$ molecules/mole
$\therefore V=\frac{4}{3} \times 3.14 \times\left(1.5 \times 10^{-8}\right)^{3} \times 6.023 \times 10^{23}=8.51 \mathrm{~cm}^{3}$
Ratio of the molecular volume to the actual volume of oxygen $=\frac{8.51}{22400}$ $=3.8 \times 10^{-4}$
Question.2 :Molar volume is the volume occupied by 1 mol of any (ideal) gas at standard temperature and pressure (STP: 1 atmospheric pressure, $0^{\circ} \mathrm{C}$ ). Show that it is $22.4$ liters.
Solution. The ideal gas equation relating pressure $(P)$, volume $(V)$, and absolute temperature $(T)$ is given as:
$P V=n R T$
Where,
$R$ is the universal gas constant $=8.314 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$
$n=$ Number of moles $=1$
$T=$ Standard temperature $=273 \mathrm{~K}$
$P=$ Standard pressure $=1 \mathrm{~atm}=1.013 \times 10^{5} \mathrm{Nm}^{-2}$
$\therefore V=\frac{n R T}{P}$
$=\frac{1 \times 8.314 \times 273}{1.013 \times 10^{5}}$
$=22.4$ litres
$=\frac{1 \times 8.314 \times 273}{1.013 \times 10^{5}}$
$=0.0224 \mathrm{~m}^{3}$
$=22.4$ litres
Hence, the molar volume of a gas at STP is $22.4$ litres.
Question.3: Figure $13.8$ shows plot of $P V I T$ versus Pfor $1.00 \times 10^{-3} \mathrm{~kg}$ of oxygen gas at two different temperatures.
Solution.

(a) What does the dotted plot signify?
(b) Which is true: $T_{1}>T_{2}$ or $T_{1}
(d) If we obtained similar plots for $1.00 \times 10^{-3} \mathrm{~kg}$ of hydrogen, would we get the same value of $P V I T$ at the point where the curves meet on the $y$ -axis? If not, what mass of hydrogen yields the same value of $P V I T$ (for low pressure high temperature region of the plot)? (Molecular mass of $\mathrm{H}_{2}=2.02 \mathrm{u}$, of $\mathrm{O}_{2}=32.0 \mathrm{u}, R=8.31 \mathrm{~J} \mathrm{mo} 1^{-1} \mathrm{~K}^{-1}$.)
Solution. (a) The dotted plot in the graph signifies the ideal behaviour of the gas, i.e., the ratio $\frac{P V}{T}$ is equal. $\mu R$ ( $\mu$ is the number of moles and $R$ is the universal gas constant) is a constant quality. It is not dependent on the pressure of the gas
(b) The dotted plot in the given graph represents an ideal gas. The curve of the gas at temperature $T_{1}$ is closer to the dotted plot than the curve of the gas at temperature $T_{2}$. A real gas approaches the behaviour of an ideal gas when its temperature increases. Therefore, $T_{1}>T_{2}$ is true for the given plot.
(c) The value of the ratio $P V I T$, where the two curves meet, is $\mu R$. This is because the ideal gas equation is given as:
$P V=\mu R T$
$\frac{P V}{T}=\mu R$
Where,
$P$ is the pressure
$T$ is the temperature
$V$ is the volume
$\mu$ is the number of moles
$R$ is the universal constant
Molecular mass of oxygen $=32.0 \mathrm{~g}$
Mass of oxygen $=1 \times 10^{-3} \mathrm{~kg}=1 \mathrm{~g}$
$R=8.314 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}$
$\therefore \frac{P V}{T}=\frac{1}{32} \times 8.314$
$=0.26 \mathrm{~J} \mathrm{~K}^{-1}$
Therefore, the value of the ratio $P V / T$, where the curves meet on the $y$ -axis, is
$0.26 \mathrm{~J} \mathrm{~K}^{-1}$
(d) If we obtain similar plots for $1.00 \times 10^{-3} \mathrm{~kg}$ of hydrogen, then we will not get the same value of $P V / T$ at the point where the curves meet the $y$ -axis. This is because the molecular mass of hydrogen $(2.02 \mathrm{u})$ is different from that of oxygen $(32.0 \mathrm{u})$.
We have:
$\frac{P V}{T}=0.26 \mathrm{~J} \mathrm{~K}^{-1}$
$R=8.314 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}$
Molecular mass $(M)$ of $\mathrm{H}_{2}=2.02 \mathrm{u}$
$\frac{P V}{T}=\mu R$ at constant temperature
Where, $\mu=\frac{m}{M}$
$m=$ Mass of $\mathrm{H}_{2}$
$\therefore m=\frac{P V}{T} \times \frac{M}{R}$
$=\frac{0.26 \times 2.02}{8.31}$
$=6.3 \times 10^{-2} \mathrm{~g}=6.3 \times 10^{-5} \mathrm{~kg}$
Hence, $6.3 \times 10^{-5} \mathrm{~kg}$ of $\mathrm{H}_{2}$ will yield the same value of $P V / T$.
Question.4: An oxygen cylinder of volume 30 litres has an initial gauge pressure of $15 \mathrm{~atm}$ and a temperature of $27^{\circ} \mathrm{C}$. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to $11 \mathrm{~atm}$ and its temperature drops to $17^{\circ} \mathrm{C}$. Estimate the mass of oxygen taken out of the cylinder $\left(R=8.31 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}\right.$, molecular mass of $\mathrm{O}_{2}=32 \mathrm{u}$ ).
Solution. Volume of oxygen, $V_{1}=30$ litres $=30 \times 10^{-3} \mathrm{~m}^{3}$
Gauge pressure, $P_{1}=15 \mathrm{~atm}=15 \times 1.013 \times 10^{5} \mathrm{~Pa}$
Temperature, $T_{1}=27^{\circ} \mathrm{C}=300 \mathrm{~K}$
Universal gas constant, $R=8.314 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}$
Let the initial number of moles of oxygen gas in the cylinder be $n_{1}$.
The gas equation is given as:
$P_{1} V_{1}=n_{1} R T_{1}$
$\therefore n_{1}=\frac{P_{1} V_{1}}{R T_{1}}$
$=\frac{15.195 \times 10^{5} \times 30 \times 10^{-3}}{(8.314) \times 300}=18.276$
But, $n_{1}=\frac{m_{1}}{M}$
Where,
$m_{1}=$ Initial mass of oxygen
$M=$ Molecular mass of oxygen $=32 \mathrm{~g}$
$\therefore m_{1}=n_{1} M=18.276 \times 32=584.84 \mathrm{~g}$
After some oxygen is withdrawn from the cylinder, the pressure and temperature reduces.
Volume, $V_{2}=30$ litres $=30 \times 10^{-3} \mathrm{~m}^{3}$
Gauge pressure, $P_{2}=11 \mathrm{~atm}=11 \times 1.013 \times 10^{5} \mathrm{~Pa}$
Temperature, $T_{2}=17^{\circ} \mathrm{C}=290 \mathrm{~K}$
Let $n_{2}$ be the number of moles of oxygen left in the cylinder.
The gas equation is given as:
$P_{2} V_{2}=n_{2} R T_{2}$
$\therefore n_{2}=\frac{P_{2} V_{2}}{R T_{2}}$
$=\frac{11.143 \times 10^{5} \times 30 \times 10^{-3}}{8.314 \times 290}=13.86$
But, $n_{2}=\frac{m_{2}}{M}$
Where,
$m_{2}$ is the mass of oxygen remaining in the cylinder
$\therefore m_{2}=n_{2} M=13.86 \times 32=453.1 \mathrm{~g}$
The mass of oxygen taken out of the cylinder is given by the relation:
Initial mass of oxygen in the cylinder $-$ Final mass of oxygen in the cylinder
$=m_{1}-m_{2}$
$=584.84 \mathrm{~g}-453.1 \mathrm{~g}$
$=131.74 \mathrm{~g}$
$=0.131 \mathrm{~kg}$
Therefore, $0.131 \mathrm{~kg}$ of oxygen is taken out of the cylinder.
Question. 5: An air bubble of volume $1.0 \mathrm{~cm}^{3}$ rises from the bottom of a lake $40 \mathrm{~m}$ deep at a temperature of $12^{\circ} \mathrm{C}$. To what volume does it grow when it reaches the surface, which is at a temperature of $35^{\circ} \mathrm{C} ?$
Solution. Volume of the air bubble, $V_{1}=1.0 \mathrm{~cm}^{3}=1.0 \times 10^{-6} \mathrm{~m}^{3}$
Bubble rises to height, $d=40 \mathrm{~m}$
Temperature at a depth of $40 \mathrm{~m}, T_{1}=12^{\circ} \mathrm{C}=285 \mathrm{~K}$
Temperature at the surface of the lake, $T_{2}=35^{\circ} \mathrm{C}=308 \mathrm{~K}$
The pressure on the surface of the lake:
$P_{2}=1 \mathrm{~atm}=1 \times 1.013 \times 10^{5} \mathrm{~Pa}$
The pressure at the depth of $40 \mathrm{~m}$ :
$P_{1}=1 \mathrm{~atm}+\mathrm{dog}$
Where,
$\rho$ is the density of water $=10^{3} \mathrm{~kg} / \mathrm{m}^{3}$
$\mathrm{g}$ is the acceleration due to gravity $=9.8 \mathrm{~m} / \mathrm{s}^{2}$
$\therefore P_{1}=1.013 \times 10^{5}+40 \times 10^{3} \times 9.8=493300 \mathrm{~Pa}$
We have: $\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}$
Where, $V_{2}$ is the volume of the air bubble when it reaches the surface
$V_{2}=\frac{P_{1} V_{1} T_{2}}{T_{1} P_{2}}$
Therefore, when the air bubble reaches the surface, its volume becomes $5.263 \mathrm{~cm}^{3}$.
Question.6: Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity $25.0 \mathrm{~m}^{3}$ at a temperature of $27^{\circ} \mathrm{C}$ and 1 atm pressure.
Solution. Volume of the room, $V=25.0 \mathrm{~m}^{3}$
Temperature of the room, $T=27^{\circ} \mathrm{C}=300 \mathrm{~K}$
Pressure in the room, $P=1 \mathrm{~atm}=1 \times 1.013 \times 10^{5} \mathrm{~Pa}$
The ideal gas equation relating pressure $(P)$, Volume $(V)$, and absolute temperature ( $T$ ) can be written as:
$P V=K_{B} N T$
Where,
$K_{B}$ is Boltzmann constant $=1.38 \times 10^{-23} \mathrm{~m}^{2} \mathrm{~kg} \mathrm{~s}^{-2} \mathrm{~K}^{-1}$
$N$ is the number of air molecules in the room $\therefore N=\frac{P V}{k_{B} T}$
$=\frac{1.013 \times 10^{5} \times 25}{1.38 \times 10^{-23} \times 300}=6.11 \times 10^{26}$ molecules
Therefore, the total number of air molecules in the given room is $6.11 \times 10^{26}$.
Question.7:Estimate the average thermal energy of a helium atom at (i) room temperature $\left(27^{\circ} \mathrm{C}\right)$, (ii) the temperature on the surface of the Sun $(6000 \mathrm{~K})$, (iii) the temperature of 10 million Kelvin (the typical core temperature in the case of a star).
Solution. (i) At room temperature, $T=27^{\circ} \mathrm{C}=300 \mathrm{~K}$
Average thermal energy $=\frac{3}{2} k T$
Where $k$ is Boltzmann constant $=1.38 \times 10^{-23} \mathrm{~J} \mathrm{~K}^{-1}$
$\therefore \frac{3}{2} k T=\frac{3}{2} \times 1.38 \times 10^{-23} \times 300 \mathrm{~J}$
$=6.21 \times 10^{-21} \mathrm{~J}$
Hence, the average thermal energy of a helium atom at room temperature $\left(27^{\circ} \mathrm{C}\right)$ is $6.21 \times 10^{-21} \mathrm{~J}$.
(ii) On the surface of the sun, $T=6000 \mathrm{~K}$ Average thermal energy $=\frac{3}{2} k T$
$=\frac{3}{2} k T=\frac{3}{2} \times 1.38 \times 10^{-23} \times 6000 \mathrm{~J}$
$=1.241 \times 10^{-19} \mathrm{~J}$ Hence, the average thermal energy of a helium atom on the surface of the sun is $1.241 \times 10^{-18} \mathrm{~J}$.
(iii) At temperature, $T=10^{7} \mathrm{~K}$
Average thermal energy $=\frac{3}{2} k T$
$=\frac{3}{2} \times 1.38 \times 10^{-23} \times 10^{7} \mathrm{~J}$
$=2.07 \times 10^{-16} \mathrm{~J}$
Hence, the average thermal energy of a helium atom at the core of a star is $2.07 \times 10^{-16} \mathrm{~J}$.
Question .8: Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contain equal number of respective molecules? Is the root mean square speed of molecules the same in the three cases? If not, in which case is $v_{r m s}$ the largest?
Solution. Yes. All contain the same number of the respective molecules.
No. The root mean square speed of neon is the largest.
Since the three vessels have the same capacity, they have the same volume.
Hence, each gas has the same pressure, volume, and temperature.
According to Avogadro's law, the three vessels will contain an equal number of the respective molecules. This number is equal to Avogadro's number, $N=6.023 \times 10^{23}$.
The root mean square speed $\left(v_{r m s}\right)$ of a gas of mass $m$, and temperature $T$, is given by the relation:
$v_{\mathrm{rms}}=\sqrt{\frac{3 k T}{m}}$
Where, $k$ is Boltzmann constant
For the given gases, $k$ and $T$ are constants.
Hence $v_{\text {rms }}$ depends only on the mass of the atoms, i.e.,
$v_{\mathrm{ms}} \propto \sqrt{\frac{1}{m}}$
Therefore, the root mean square speed of the molecules in the three cases is not the same. Among neon, chlorine, and uranium hexafluoride, the mass of neon is the smallest. Hence, neon has the largest root mean square speed among the given gases.
Question.9:At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at $-20^{\circ} \mathrm{C} ?$ (atomic mass of $\mathrm{Ar}=39.9 \mathrm{u}$, of $\mathrm{He}=4.0 \mathrm{u}$ ).
Solution. Temperature of the helium atom, $T_{\mathrm{He}}=-20^{\circ} \mathrm{C}=253 \mathrm{~K}$
Atomic mass of argon, $M_{\mathrm{Ar}}=39.9 \mathrm{u}$
Atomic mass of helium, $M_{\mathrm{He}}=4.0 \mathrm{u}$
Let, $\left(V_{r m s}\right)_{A r}$ be the rms speed of argon.
Let $\left(V_{\text {rms }}\right)_{\mathrm{He}}$ be the rms speed of helium.
The rms speed of argon is given by:
$\left(v_{r m s}\right)_{A r}=\sqrt{\frac{3 R T_{A r}}{M_{A r}}} \ldots(i)$
Where,
$R$ is the universal gas constant
$T_{\mathrm{Ar}}$ is temperature of argon gas
The rms speed of helium is given by:
$\left(v_{\mathrm{mos}}\right)_{\mathrm{He}}=\sqrt{\frac{3 R T_{\mathrm{He}}}{M_{\mathrm{He}}}} \ldots$ (ii)
It is given that:
$\left(V_{\mathrm{rms}}\right)_{\mathrm{Ar}}=\left(V_{\mathrm{rms}}\right)_{\mathrm{He}}$
$\sqrt{\frac{3 R T_{\mathrm{Ar}}}{M_{\mathrm{Ar}}}}=\sqrt{\frac{3 R T_{\mathrm{He}}}{M_{\mathrm{He}}}}$
$\frac{T_{\mathrm{Ar}}}{M_{\mathrm{Ar}}}=\frac{T_{\mathrm{He}}}{M_{\mathrm{H}_{e}}}$
$T_{\mathrm{At}}=\frac{T_{\mathrm{HC}}}{M_{\mathrm{Hc}}} \times M_{\mathrm{Ar}}$
$=\frac{253}{4} \times 39.9$
$=2523.675=2.52 \times 10^{3} \mathrm{~K}$
Therefore, the temperature of the argon atom is $2.52 \times 10^{3} \mathrm{~K}$.
Question.10: Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at $2.0 \mathrm{~atm}$ and temperature $17^{\circ} \mathrm{C}$. Take the radius of a nitrogen molecule to be roughly $1.0$ Á. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of $\mathrm{N}_{2}=28.0 \mathrm{u}$ ).
Solution. Mean free path $=1.11 \times 10^{-7} \mathrm{~m}$
Collision frequency $=4.58 \times 10^{9} \mathrm{~s}^{-1}$
Successive collision time $\approx 500 \times$ (Collision time)
Pressure inside the cylinder containing nitrogen, $P=2.0 \mathrm{~atm}=2.026 \times 10^{5} \mathrm{~Pa}$
Temperature inside the cylinder, $T=17^{\circ} \mathrm{C}=290 \mathrm{~K}$
Radius of a nitrogen molecule, $r=1.0 \mathrm{~A}=1 \times 10^{10} \mathrm{~m}$
Diameter, $d=2 \times 1 \times 10^{10}=2 \times 10^{10} \mathrm{~m}$
Molecular mass of nitrogen, $M=28.0 \mathrm{~g}=28 \times 10^{-3} \mathrm{~kg}$
The root mean square speed of nitrogen is given by the relation:
$v_{\mathrm{rms}}=\sqrt{\frac{3 R T}{M}}$
Where,
$R$ is the universal gas constant $=8.314 \mathrm{~J}$ mole $^{-1} \mathrm{~K}^{-1}$
$\therefore v_{\mathrm{ms}}=\sqrt{\frac{3 \times 8.314 \times 290}{28 \times 10^{-3}}}=508.26 \mathrm{~m} / \mathrm{s}$
The mean free path ( $I$ ) is given by the relation:
$I=\frac{k T}{\sqrt{2} \times d^{2} \times P}$
Where,
$k$ is the Boltzmann constant $=1.38 \times 10^{-23} \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-2} \mathrm{~K}^{-1}$
$\therefore I=\frac{1.38 \times 10^{-23} \times 290}{\sqrt{2} \times 3.14 \times\left(2 \times 10^{-10}\right)^{2} \times 2.026 \times 10^{5}}$
$=1.11 \times 10^{-7} \mathrm{~m}$
Collision frequency $=\frac{v_{r m s}}{l}$
$=\frac{508.26}{1.11 \times 10^{-7}}=4.58 \times 10^{9} \mathrm{~s}^{-1}$
Collision time is given as:
$T=\frac{d}{v_{\mathrm{rms}}}$
$=\frac{2 \times 10^{-10}}{508.26}=3.93 \times 10^{-13} \mathrm{~S}$
Time taken between successive collisions:
$T^{\prime}=\frac{l}{v_{\mathrm{rms}}}$
$=\frac{1.11 \times 10^{-7} \mathrm{~m}}{508.26 \mathrm{~m} / \mathrm{s}}=2.18 \times 10^{-10} \mathrm{~s}$
$\therefore \frac{T^{\prime}}{T}=\frac{2.18 \times 10^{-10}}{3.93 \times 10^{-13}}=500$
Hence, the time taken between successive collisions is 500 times the time taken for a collision.
Question.11:A metre long narrow bore held horizontally (and closed at one end) contains a $76 \mathrm{~cm}$ long mercury thread, which traps a $15 \mathrm{~cm}$ column of air. What happens if the tube is held vertically with the open end at the bottom?
Solution. Length of the narrow bore, $L=1 \mathrm{~m}=100 \mathrm{~cm}$
Length of the mercury thread, $/=76 \mathrm{~cm}$
Length of the air column between mercury and the closed end, $l_{a}=15 \mathrm{~cm}$
Since the bore is held vertically in air with the open end at the bottom, the mercury length that occupies the air space is: $100-(76+15)=9 \mathrm{~cm}$
Hence, the total length of the air column $=15+9=24 \mathrm{~cm}$
Let $h \mathrm{~cm}$ of mercury flow out as a result of atmospheric pressure.
$\therefore$ Length of the air column in the bore $=24+h \mathrm{~cm}$
And, length of the mercury column $=76-h \mathrm{~cm}$
Initial pressure, $P_{1}=76 \mathrm{~cm}$ of mercury
Initial volume, $V_{1}=15 \mathrm{~cm}^{3}$
Final pressure, $P_{2}=76-(76-h)=h \mathrm{~cm}$ of mercury
Final volume, $V_{2}=(24+h) \mathrm{cm}^{3}$
Temperature remains constant throughout the process.
$\therefore P_{1} V_{1}=P_{2} V_{2}$
$76 \times 15=h(24+h)$
$h^{2}+24 h-1140=0$
$\therefore h=\frac{-24 \pm \sqrt{(24)^{2}+4 \times 1 \times 1140}}{2 \times 1}$
$=23.8 \mathrm{~cm}$ or $-47.8 \mathrm{~cm}$
Height cannot be negative. Hence, $23.8 \mathrm{~cm}$ of mercury will flow out from the bore and $52.2 \mathrm{~cm}$ of mercury will remain in it. The length of the air column will be $24+23.8=47.8 \mathrm{~cm}$.
Question.12: From a certain apparatus, the diffusion rate of hydrogen has an average value of $28.7 \mathrm{~cm}^{3} \mathrm{~s}^{-1}$. The diffusion of another gas under the same conditions is measured to have an average rate of $7.2 \mathrm{~cm}^{3}$ $\mathrm{s}^{-1}$. Identify the gas.
[Hint: Use Graham's law of diffusion: $\mathrm{R}_{1} / \mathrm{R}_{2}=\left(\mathrm{M}_{2} / \mathrm{M}_{1}\right)^{1 / 2}$, where $\mathrm{R}_{1}, \mathrm{R}_{2}$ are diffusion rates of gases 1 and 2, and $\mathrm{M}_{1}$ and $\mathrm{M}_{2}$ their respective molecular masses. The law is a simple consequence of kinetic theory.]
Solution. Rate of diffusion of hydrogen, $R_{1}=28.7 \mathrm{~cm}^{3} \mathrm{~s}^{-1}$
Rate of diffusion of another gas, $R_{2}=7.2 \mathrm{~cm}^{3} \mathrm{~s}^{-1}$
According to Graham's Law of diffusion, we have:
$\frac{R_{1}}{R_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}$
$=2.02\left(\frac{28.7}{7.2}\right)^{2}=32.09 \mathrm{~g}$
$32 \mathrm{~g}$ is the molecular mass of oxygen. Hence, the unknown gas is oxygen.
Question.13 A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so-called law of atmospheres
$n_{2}=n_{1} \exp \left[-m g\left(h_{2}-h_{1}\right) / k_{B} T\right]$
Where $n_{2}, n_{1}$ refer to number density at heights $h_{2}$ and $h_{1}$ respectively. Use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid column:
$n_{2}=n_{1} \exp \left[-m g N_{A}\left(\rho-P^{\prime}\right)\left(h_{2}-h_{1}\right) /(\rho R T)\right]$
Where $\rho$ is the density of the suspended particle, and $\rho$ ' that of surrounding medium. $\left[N_{A}\right.$ is Avogadro's number, and $R$ the universal gas constant.] [Hint: Use Archimedes principle to find the apparentweight of the suspended particle.]
Solution. According to the law of atmospheres, we have:
$n_{2}=n_{1} \exp \left[-m g\left(h_{2}-h_{1}\right) / k B T\right] \ldots(i)$
Where,
$n_{1}$ is thenumber density at height $h_{1}$, and $n_{2}$ is the number density at height $h_{2}$
$m g$ is the weight of the particle suspended in the gas column
Density of the medium $=\rho^{\prime}$
Density of the suspended particle $=\rho$
Mass of one suspended particle $=m^{\prime}$
Mass of the medium displaced $=m$
Volume of a suspended particle $=V$
According to Archimedes' principle for a particle suspended in a liquid column, the effective weight of the suspended particle is given as:
Weight of the medium displaced - Weight of the suspended particle
$=m g-m^{\prime} g$
$=m g-V \rho^{\prime} g=m g-\left(\frac{m}{\rho}\right) \rho^{\prime} g$
$=m g\left(1-\frac{\rho^{\prime}}{\rho}\right) \quad \ldots(i i)$
Gas constant, $R=k_{B} N$
$k_{s}=\frac{R}{N} \ldots$ (iii)
Substituting equation (ii) in place of $m g$ in equation $(i)$ and then using equation (iii), we get:
$n_{2}=n_{1} \exp \left[-m g\left(h_{2}-h_{1}\right) / k_{B} T\right]$
$=n_{1} \exp \left[-m g\left(1-\frac{\rho^{\prime}}{\rho}\right)\left(h_{2}-h_{1}\right) \frac{N}{R T}\right]$
$=n_{1} \exp \left[-m g\left(\rho-\rho^{\prime}\right)\left(h_{2}-h_{1}\right) \frac{N}{R T \rho}\right]$
Question.14: Given below are densities of some solids and liquids. Give rough estimates of the size of their atoms:

[Hint: Assume the atoms to be 'tightly packed' in a solid or liquid phase, and use the known value of Avogadro's number. You should, however, not take the actual numbers you obtain for various atomic sizes too literally. Because of the crudeness of the tight packing approximation, the results only indicate that atomic sizes are in the range of a few $$.
Solution.

Atomic mass of a substance $=M$
Density of the substance $=\rho$
Avogadro's number $=N=6.023 \times 10^{23}$
Volume of each atom $=\frac{4}{3} \pi r^{3}$
Volume of $N$ number of molecules $=\frac{4}{3} \pi r^{3} N \ldots(i)$
Volume of one mole of a substance $=\frac{M}{\rho} \ldots$ (ii)
$\frac{4}{3} \pi r^{3} N=\frac{M}{\rho}$
$\therefore r=\sqrt[3]{\frac{3 M}{4 \pi \rho N}}$
For carbon:
$M=12.01 \times 10^{-3} \mathrm{~kg}$,
$\rho=2.22 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 12.01 \times 10^{-3}}{4 \pi \times 2.22 \times 10^{3} \times 6.023 \times 10^{23}}\right)^{\frac{1}{3}}=1.29 \mathrm{~A}$
Hence, the radius of a carbon atom is $1.29$.
For gold:
$M=197.00 \times 10^{-3} \mathrm{~kg}$
$\rho=19.32 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 197 \times 10^{-3}}{4 \pi \times 19.32 \times 10^{3} \times 6.023 \times 10^{23}}\right)^{\frac{1}{3}}=1.59 \AA{A}$
Hence, the radius of a gold atom is $1.59$.
For liquid nitrogen:
$M=14.01 \times 10^{-3} \mathrm{~kg}$
$\rho=1.00 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 14.01 \times 10^{-3}}{4 \pi \times 1.00 \times 10^{3} \times 6.23 \times 10^{23}}\right)^{\frac{1}{3}}=1.77 \AA$
Hence, the radius of a liquid nitrogen atom is $1.77 \AA$.
For lithium:
$M=6.94 \times 10^{-3} \mathrm{~kg}$
$\rho=0.53 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 6.94 \times 10^{-3}}{4 \pi \times 0.53 \times 10^{3} \times 6.23 \times 10^{23}}\right)^{\frac{1}{3}}=1.73 \mathrm{~A}$
Hence, the radius of a lithium atom is $1.73 \AA{A}$.
For liquid fluorine:
$M=19.00 \times 10^{-3} \mathrm{~kg}$
$\rho=1.14 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$
$\therefore r=\left(\frac{3 \times 19 \times 10^{-3}}{4 \pi \times 1.14 \times 10^{3} \times 6.023 \times 10^{23}}\right)^{\frac{1}{3}}=1.88 \AA$
Hence, the radius of a liquid fluorine atom is $1.88 \mathrm{~A}$.
So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.
Also Read,
Download Class 11 Physics Notes Free PDF
Download Class 11 Physics Book Chapterwise Free PDF
Download Class 11 Physics Exemplar Chapterwise Free PDF
If you have any Confusion related to NCERT Solutions for Class 11 Physics chapter 13 then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 11 Physics by Kota’s top IITian’s Faculties Install the eSaral App
