
Hey, are you a class 11 student and looking for ways to download NCERT Solutions for Class 11 Chemistry chapter 7 Equilibrium PDF? If yes. Then read this post till the end.
In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 7 Equilibrium in PDF that are prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to learn and understand class 11 Chemistry chapter 7 "Equilibrium" in an easy way then you can use these solutions PDF.
NCERT Solutions helps students to Practice important concepts of subjects easily. Class 11 Chemistry solutions provide detailed explanations of all the NCERT questions that students can use to clear their doubts instantly.
If you want to score high in your class 11 Chemistry Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.
In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 7 Equilibrium PDF that you can download to start your preparations anytime.
So, without wasting more time Let’s start.
a) What is the initial effect of the change on vapour pressure?
b) How do rates of evaporation and condensation change initially?
c) What happens when equilibrium is restored finally and what will be the final vapour pressure?
Solution . (a) If the volume of the container is suddenly increased, then the vapour pressure would decrease initially. This is because the amount of vapour remains the same, but the volume increases suddenly. As a result, the same amount of vapour is distributed in a larger volume
(b) Since the temperature is constant, the rate of evaporation also remains constant. When the volume of the container is increased, the density of the vapour phase decreases. As a result, the rate of collisions of the vapour particles also decreases. Hence, the rate of condensation decreases initially.
(c) When equilibrium is restored finally, the rate of evaporation becomes equal to the rate of condensation. In this case, only the volume changes while the temperature remains constant. The
vapour pressure depends on temperature and not on volume. Hence, the final vapour pressure will be equal to the original vapour pressure of the system
Question 2: What is $K_{c}$ for the following equilibrium when the equilibrium concentration of each substance is: $\left[\mathrm{SO}_{2}\right]=0.60 \mathrm{M},\left[\mathrm{O}_{2}\right]=0.82 \mathrm{M}$ and $\left[\mathrm{SO}_{3}\right]=1.90 \mathrm{M} ?$
Solution. The equilibrium constant $\left(\mathrm{K}_{c}\right)$ for the give reaction is:
$\mathrm{K}_{c}=\frac{\left[\mathrm{SO}_{3}\right]^{2}}{\left[\mathrm{SO}_{2}\right]^{2}\left[\mathrm{O}_{2}\right]}$
$=\frac{(1.90)^{2} \mathrm{M}^{2}}{(0.60)^{2}(0.821) \mathrm{M}^{3}}$
$=12.239 \mathrm{M}^{-1}$ (approximately)
Hence, $K_{c}$ for the equilibrium is $12.239 \mathrm{M}^{-1}$.
Question 3: At a certain temperature and total pressure of $10^{5} \mathrm{~Pa}$, iodine vapour contains $40 \%$ by volume of $\mathrm{I}$ atoms
$\mathrm{I}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{I}(\mathrm{g})$
Calculate $K_{p}$ for the equilibrium.
Solution. Partial pressure of I atoms,
$p_{1}=\frac{40}{100} \times p_{\text {total }}$
$=\frac{40}{100} \times 10^{5}$
$=4 \times 10^{4} \mathrm{~Pa}$
Partial pressure of $\mathrm{I}_{2}$ molecules,
$p_{\mathrm{I}_{2}}=\frac{60}{100} \times p_{\text {total }}$
$=\frac{60}{100} \times 10^{5}$
$=6 \times 10^{4} \mathrm{~Pa}$
Now, for the given reaction,
$K_{p}=\frac{(p \mathrm{I})^{2}}{p_{1_{2}}}$
$=\frac{\left(4 \times 10^{4}\right)^{2} \mathrm{~Pa}^{2}}{6 \times 10^{4} \mathrm{~Pa}}$
$=2.67 \times 10^{4} \mathrm{~Pa}$
Question 4: Write the expression for the equilibrium constant, $K_{c}$ for each of the following
Write the expression for the equilibrium constant, $K_{c}$ for each of the following
reactions:
(i) $2 \mathrm{NOCl}(\mathrm{g}) \longleftrightarrow 2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl}_{2}(\mathrm{~g})$
(ii) $2 \mathrm{Cu}\left(\mathrm{NO}_{3}\right)_{2}(\mathrm{~s}) \longleftrightarrow 2 \mathrm{CuO}(\mathrm{s})$
$+4 \mathrm{NO}_{2}(\mathrm{~g})+\mathrm{O}_{2}(\mathrm{~g})$
(iii) $\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}(\mathrm{aq})+\mathrm{H}_{2} \mathrm{O}(\mathrm{l}) \longleftrightarrow$
$\mathrm{CH}_{3} \mathrm{COOH}(\mathrm{aq})+\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}(\mathrm{aq})$
(iv) $\mathrm{Fe}^{3+}(\mathrm{aq})+3 \mathrm{OH}^{-}(\mathrm{aq}) \longleftrightarrow \mathrm{Fe}(\mathrm{OH})_{3}(\mathrm{~s})$
(v) $\mathrm{I}_{2}(\mathrm{~s})+5 \mathrm{~F}_{2} \longleftrightarrow 2 \mathrm{IF}_{5}$
Solution.(i)$K_{c}=\frac{\left[\mathrm{NO}_{(g)}\right]^{2}\left[\mathrm{Cl}_{2(g)}\right]}{\left[\mathrm{NOCl}_{(g)}\right]^{2}}$
(ii) $\quad K_{c}=\frac{\left[\mathrm{CuO}_{(s)}\right]^{2}\left[\mathrm{NO}_{2(g)}\right]^{4}\left[\mathrm{O}_{2(g)}\right]}{\left[\mathrm{Cu}\left(\mathrm{NO}_{3}\right)_{2(s)}\right]^{2}}$
$=\left[\mathrm{NO}_{2(g)}\right]^{4}\left[\mathrm{O}_{2(g)}\right]$
(iii) $K_{c}=\frac{\left[\mathrm{CH}_{3} \mathrm{COOH}_{(a q)}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}_{(a q)}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5(a q)}\right]\left[\mathrm{H}_{2} \mathrm{O}_{(t)}\right]}$
$=\frac{\left[\mathrm{CH}_{3} \mathrm{COOH}_{(a q)}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}_{(a q)}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5(a q)}\right]}$
(iv) $K_{c}=\frac{\left[\mathrm{Fe}(\mathrm{OH})_{3(s)}\right]}{\left[\mathrm{Fe}_{(a g)}\right]\left[\mathrm{OH}_{(a q)}^{-}\right]^{3+}}$
$=\frac{1}{\left[\mathrm{Fe}^{3+}{ }_{(o q)}\right]\left[\mathrm{OH}_{(a q)}^{-}\right]^{3}}$
(v)$K_{c}=\frac{\left[\mathrm{IF}_{5}\right]^{2}}{\left[\mathrm{I}_{2(s)}\right]\left[\mathrm{F}_{2}\right]^{5}}$
$=\frac{\left[\mathrm{IF}_{5}\right]^{2}}{\left[\mathrm{~F}_{2}\right]^{5}}$
Question 5: Find out the value of $K_{c}$ for each of the following equilibria from the value of $K_{p}$ :
(i) $2 \mathrm{NOCl}(\mathrm{g}) \longleftrightarrow 2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl}_{2}(\mathrm{~g})$;
$K_{p}=1.8 \times 10^{-2}$ at $500 \mathrm{~K}$
(ii) $\mathrm{CaCO}_{3}(\mathrm{~s}) \longleftrightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g}) ;$
$\mathrm{K}_{p}=167$ at $1073 \mathrm{~K}$
Solution. The relation between $K_{p}$ and $K_{c}$ is given as:
$K_{p}=K_{c}(\mathrm{RT})^{\Delta n}$
(a) Here,
$\Delta n=3-2=1$
$R=0.0831$ barLmol $^{-1} \mathrm{~K}^{-1}$
$T=500 \mathrm{~K}$
$K_{p}=1.8 \times 10^{-2}$
Now,
$K_{p}=K_{c}(R T)^{\Delta n}$
$\Rightarrow 1.8 \times 10^{-2}=K_{c}(0.0831 \times 500)^{1}$
$\Rightarrow K_{c}=\frac{1.8 \times 10^{-2}}{0.0831 \times 500}$
$=4.33 \times 10^{-4}$ (approximately)
(b) Here,
$\Delta n=2-1=1$
$R=0.0831$ barLmol $^{-1} K^{-1}$
$T=1073 \mathrm{~K}$
$K_{p}=167$
Now,
$K_{p}=K_{c}(R T)^{\Delta n}$
$\Rightarrow 167=K_{c}(0.0831 \times 1073)^{\Delta n}$
$\Rightarrow K_{c}=\frac{167}{0.0831 \times 1073}$
$=1.87$ (approximately)
Question 6: For the following equilibrium, $K_{\mathrm{C}}=6.3 \times 10^{14}$ at $1000 \mathrm{~K}$
$\mathrm{NO}(\mathrm{g})+\mathrm{O}_{3}(\mathrm{~g}) \longleftrightarrow \mathrm{NO}_{2}(\mathrm{~g})+\mathrm{O}_{2}(\mathrm{~g})$
Both the forward and reverse reactions in the equilibrium are elementary bimolecular reactions. What is $K_{c}$, for the reverse reaction?
Solution. It is given that $K_{C}$ for the forward reaction is $6.3 \times 10^{14}$.
Then, $K_{C}$ for the reverse reaction will be,
$K_{C}^{\prime}=\frac{1}{K_{C}}$
$=\frac{1}{6.3 \times 10^{14}}$
$=1.59 \times 10^{-15}$
Question 7: Explain why pure liquids and solids can be ignored while writing the equilibrium constant expression?
Solution. For a pure substance (both solids and liquids),
[Pure substance $]=\frac{\text { Number of moles }}{\text { Volume }}$
$=\frac{\text { Mass/molecular mass }}{\text { Volume }}$
$=\frac{\text { Mass }}{\text { Volume } \times \text { Molecular mass }}$
$=\frac{\text { Density }}{\text { Molecular mass }}$
Now, the molecular mass and density (at a particular temperature) of a pure substance is always fixed and is accounted for in the equilibrium constant. Therefore, the values of pure substances are not mentioned in the equilibrium constant expression.
Question 8: Reaction between $\mathrm{N}_{2}$ and $\mathrm{O}_{2}$ takes place as follows:
$2 \mathrm{~N}_{2}(\mathrm{~g})+\mathrm{O}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{~N}_{2} \mathrm{O}(\mathrm{g})$
If a mixture of $0.482$ mol of $\mathrm{N}_{2}$ and $0.933 \mathrm{~mol}$ of $\mathrm{O}_{2}$ is placed in a $10 \mathrm{~L}$ reaction vessel and allowed to form $\mathrm{N}_{2} \mathrm{O}$ at a temperature for which $K_{c}=2.0 \times 10^{-37}$, determine the composition of equilibrium mixture.
Solution. Let the concentration of $\mathrm{N}_{2} \mathrm{O}$ at equilibrium be $x$.
The given reaction is:
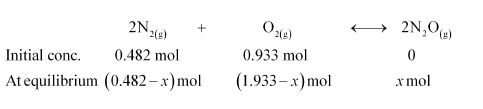
Therefore, at equilibrium, in the $10 \mathrm{~L}$ vessel:
$\left[\mathrm{N}_{2}\right]=\frac{0.482-x}{10},\left[\mathrm{O}_{2}\right]$
$=\frac{0.933-x / 2}{10},\left[\mathrm{~N}_{2} \mathrm{O}\right]=\frac{x}{10}$
The value of equilibrium constant i.e., $K_{c}=2.0 \times 10^{-37}$ is very small. Therefore, the amount of $\mathrm{N}_{2}$ and $\mathrm{O}_{2}$ reacted is also very small. Thus, $x$ can be neglected from the expressions of molar concentrations of $\mathrm{N}_{2}$ and $\mathrm{O}_{2}$
Then,
$\left[\mathrm{N}_{2}\right]=\frac{0.482}{10}=0.0482 \mathrm{~mol} \mathrm{~L}^{-1}$
and $\left[\mathrm{O}_{2}\right]=\frac{0.933}{10}=0.0933 \mathrm{~mol} \mathrm{~L}^{-1}$
Now.
$K_{\mathrm{C}}=\frac{\left[\mathrm{N}_{2} \mathrm{O}_{(\mathrm{g})}\right]^{2}}{\left[\mathrm{~N}_{2(\mathrm{~g})}\right]^{2}\left[\mathrm{O}_{2(\mathrm{~g})}\right]}$
$\Rightarrow 2.0 \times 10^{-37}=\frac{\left(\frac{x}{10}\right)^{2}}{(0.0482)^{2}(0.0933)}$
$\Rightarrow \frac{x^{2}}{100}=2.0 \times 10^{-37} \times(0.0482)^{2} \times(0.0933)$
$\Rightarrow x^{2}=43.35 \times 10^{-40}$
$\Rightarrow x=6.6 \times 10^{-20}$
$\left[\mathrm{N}_{2} \mathrm{O}\right]=\frac{x}{10}=\frac{6.6 \times 10^{-20}}{10}$
$=6.6 \times 10^{-21}$
Question 9: Nitric oxide reacts with $\mathrm{Br}_{2}$ and gives nitrosyl bromide as per reaction given below:
$2 \mathrm{NO}(\mathrm{g})+\mathrm{Br}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{NOBr}(\mathrm{g})$
When $0.087$ mol of NO and $0.0437$ mol of $\mathrm{Br}_{2}$ are mixed in a closed container at constant temperature, $0.0518$ mol of NOBr is obtained at equilibrium. Calculate equilibrium amount of $\mathrm{NO}$ and $\mathrm{Br}_{2}$.
Solution. The given reaction is:

Now, 2 mol of NOBr are formed from 2 mol of NO. Therefore, $0.0518$ mol of NOBr are formed from $0.0518$ mol of NO.
Again, 2 mol of NOBr are formed from 1 mol of Br.
Therefore, $0.0518$ mol of $\mathrm{NOBr}$ are formed from $\frac{0.0518}{2}$ mol of $\mathrm{Br}$, or
$0.0259$ mol of NO.
The amount of NO and Br present initially is as follows:
$[\mathrm{NO}]=0.087 \mathrm{~mol}\left[\mathrm{Br}_{2}\right]=0.0437 \mathrm{~mol}$
Therefore, the amount of NO present at equilibrium is:
$[\mathrm{NO}]=0.087-0.0518$
$=0.0352 \mathrm{~mol}$
And, the amount of Br present at equilibrium is:
$\left[\mathrm{Br}_{2}\right]=0.0437-0.0259$
$=0.0178 \mathrm{~mol}$
Question 10: At $450 \mathrm{~K}, K_{\mathrm{p}}=2.0 \times 10^{10} / \mathrm{bar}$ for the given reaction at equilibrium.
$2 \mathrm{SO}_{2(g)}+\mathrm{O}_{2(g)} \longleftrightarrow 2 \mathrm{SO}_{3(g)}$
What is $K_{c}$ at this temperature?
Solution. For the given reaction,
$\Delta n=2-3=-1$
$T=450 \mathrm{~K}$
$R=0.0831$ bar $\mathrm{L}$ bar $\mathrm{K}^{-1} \mathrm{~mol}^{-1}$
$K_{\mathrm{p}}=2.0 \times 10^{10} \mathrm{bar}^{-1}$
We know that,
$K_{\mathrm{P}}=K_{\mathrm{C}}(R T) \Delta n$
$\Rightarrow 2.0 \times 10^{10} \mathrm{bar}^{-1}$
$=K_{C}\left(0.0831 \mathrm{~L} \mathrm{bar} \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 450 \mathrm{~K}\right)^{-1}$
$\Rightarrow K_{\mathrm{C}}=\frac{2.0 \times 10^{10} \mathrm{bar}^{-1}}{\left(0.0831 \mathrm{~L} \text { bar } \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 450 \mathrm{~K}\right)^{-1}}$
$=\left(2.0 \times 10^{10} \mathrm{bar}^{-1}\right)\left(0.0831 \mathrm{~L} \mathrm{bar} \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 450 \mathrm{~K}\right)$
$=74.79 \times 10^{10} \mathrm{~L} \mathrm{~mol}^{-1}$
$=7.48 \times 10^{11} \mathrm{~L} \mathrm{~mol}^{-1}$
$=7.48 \times 10^{11} \mathrm{M}^{-1}$
Question 11: A sample of $\mathrm{HI}_{(\mathrm{g})}$ is placed in flask at a pressure of $0.2 \mathrm{~atm}$. At equilibrium the partial pressure of $\mathrm{HI}_{(\mathrm{g})}$ is $0.04 \mathrm{~atm} .$ What is $K_{\mathrm{p}}$ for the given equilibrium?
$2 \mathrm{HI}(\mathrm{g}) \longleftrightarrow \mathrm{H}_{2}(\mathrm{~g})+\mathrm{I}_{2}(\mathrm{~g})$
Solution. The initial concentration of HI is $0.2$ atm. At equilibrium, it has a partial pressure of $0.04$ atm. Therefore, a decrease in the pressure of $\mathrm{Hl}$ is $0.2-0.04=0.16$. The given reaction is:

Therefore,
$K_{\mathrm{p}}=\frac{p_{\mathrm{H}_{2}} \times p_{\mathrm{I}_{2}}}{p_{\mathrm{HI}}^{2}}$
$=\frac{0.08 \times 0.08}{(0.04)^{2}}$
$=\frac{0.0064}{0.0016}$
$=4.0$
Hence, the value of $K_{\mathrm{p}}$ for the given equilibrium is $4.0$.
Question $12$ : A mixture of $1.57 \mathrm{~mol}$ of $\mathrm{N}_{2}, 1.92 \mathrm{~mol}$ of $\mathrm{H}_{2}$ and $8.13 \mathrm{~mol}$ of $\mathrm{NH}_{3}$ is introduced into a $20 \mathrm{~L}$ reaction vessel at $500 \mathrm{~K}$. At this temperature, the equilibrium constant, $K_{c}$ for the reaction $\mathrm{N}_{2}(\mathrm{~g})+3 \mathrm{H}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{NH}_{3}(\mathrm{~g})$ is $1.7 \times 10^{2}$
Is the reaction mixture at equilibrium? If not, what is the direction of the net reaction?
Solution. The given reaction is:
$\mathrm{N}_{2(\mathrm{~g})}+3 \mathrm{H}_{2(\mathrm{~g})} \longleftrightarrow 2 \mathrm{NH}_{3(\mathrm{~g})}$
The given concentration of various species is
$\left[\mathrm{N}_{2}\right]=\frac{1.57}{20} \mathrm{~mol} \mathrm{~L}^{-1}$
$\left[\mathrm{H}_{2}\right]=\frac{1.92}{20} \mathrm{~mol} \mathrm{~L}^{-}$
$\left[\mathrm{NH}_{3}\right]=\frac{8.13}{20} \mathrm{~mol} \mathrm{~L}^{-}$
Now, reaction quotient $Q_{c}$ is:
$Q_{\mathrm{C}}=\frac{\left[\mathrm{NH}_{3}\right]^{2}}{\left[\mathrm{~N}_{2}\right]\left[\mathrm{H}_{2}\right]^{3}}$
$=\frac{\left(\frac{(8.13)}{20}\right)^{2}}{\left(\frac{1.57}{20}\right)\left(\frac{1.92}{20}\right)^{3}}$
$=2.4 \times 10^{3}$
Since $Q_{\mathrm{C}} \neq K_{\mathrm{C}}$, the reaction mixture is not at equilibrium.
Again, $Q_{\mathrm{C}}>K_{\mathrm{c}}$. Hence, the reaction will proceed in the reverse direction.
Question 13: The equilibrium constant expression for a gas reaction is,
$K_{\mathrm{C}}=\frac{\left[\mathrm{NH}_{3}\right]^{4}\left[\mathrm{O}_{2}\right]^{5}}{[\mathrm{NO}]^{4}\left[\mathrm{H}_{2} \mathrm{O}\right]^{6}}$
Write the balanced chemical equation corresponding to this expression.
Solution. The balanced chemical equation corresponding to the given expression can be written as:
$4 \mathrm{NO}_{(g)}+6 \mathrm{H}_{2} \mathrm{O}_{(g)} \longleftrightarrow 4 \mathrm{NH}_{3(g)}+5 \mathrm{O}_{2(g)}$
Question 14:One mole of $\mathrm{H}_{2} \mathrm{O}$ and one mole of $\mathrm{CO}$ are taken in $10 \mathrm{~L}$ vessel and heated to
$725 \mathrm{~K}$. At equilibrium $40 \%$ of water (by mass) reacts with $\mathrm{CO}$ according to the equation,
$\mathrm{H}_{2} \mathrm{O}(\mathrm{g})+\mathrm{CO}(\mathrm{g}) \longleftrightarrow \mathrm{H}_{2}(\mathrm{~g})+\mathrm{CO}_{2}(\mathrm{~g})$
Calculate the equilibrium constant for the reaction.
Solution. The given reaction is:
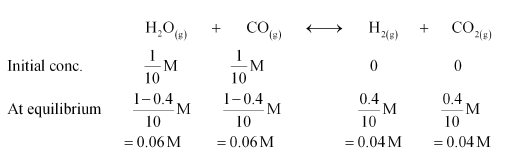
Therefore, the equilibrium constant for the reaction,
$K_{\mathrm{C}}=\frac{\left[\mathrm{H}_{2}\right]\left[\mathrm{CO}_{2}\right]}{\left[\mathrm{H}_{2} \mathrm{O}\right][\mathrm{CO}]}$
$=\frac{0.04 \times 0.04}{0.06 \times 0.06}$
$=0.444$ (approximately)
Question $15$ : At $700 \mathrm{~K}$, equilibrium constant for the reaction
$\mathrm{H}_{2(g)}+\mathrm{I}_{2(g)} \longleftrightarrow 2 \mathrm{HI}_{(g)}$
is $54.8$. If $0.5 \mathrm{molL}^{-1}$ of $\mathrm{HI}_{(g)}$ is present at equilibrium at $700 \mathrm{~K}$, what are the concentration of $\mathrm{H}_{2(g)}$ and $\mathrm{I}_{2(g)}$ assuming that we initially started with $\mathrm{HI}_{(g)}$ and allowed it to reach equilibrium at $700 \mathrm{~K} ?$
Solution. It is given that equilibrium constant $K_{\mathrm{c}}$ for the reaction
$\mathrm{H}_{2(g)}+\mathrm{I}_{2(g)} \longleftrightarrow 2 \mathrm{HI}_{(g)}$ is $54.8$
Therefore, at equilibrium, the equilibrium constant $K_{\mathrm{c}}^{\prime}$ for the reaction
$2 \mathrm{HI}_{(\mathrm{g})} \longleftrightarrow \mathrm{H}_{2(\mathrm{~g})}+\mathrm{I}_{2(\mathrm{~g})}$ will be $\frac{1}{54.8} .$
$[\mathrm{HI}]=0.5 \mathrm{molL}^{-1}$
Let the concentrations of hydrogen and iodine at equilibrium be $x \mathrm{molL}^{-1}$
$\left[\mathrm{H}_{2}\right]=\left[\mathrm{I}_{2}\right]=x \mathrm{~mol} \mathrm{~L}^{-1}$
Therefore,
$\frac{\left[\mathrm{H}_{2}\right]\left[\mathrm{I}_{2}\right]}{[\mathrm{HI}]^{2}}=K_{\mathrm{C}}^{\prime}$
$\Rightarrow \frac{x \times x}{(0.5)^{2}}=\frac{1}{54.8}$
$\Rightarrow x^{2}=\frac{0.25}{54.8}$
$\Rightarrow x=0.06754$
$x=0.068 \mathrm{molL}^{-1}$ (approximately)
Hence, at equilibrium, $\left[\mathrm{H}_{2}\right]=\left[\mathrm{I}_{2}\right]=0.068 \mathrm{~mol} \mathrm{~L}^{-1}$.
Question 16: What is the equilibrium concentration of each of the substances in the equilibrium when the initial concentration of ICl was $0.78 \mathrm{M}$ ?
$2 \mathrm{Cl}(\mathrm{g}) \rightleftharpoons \mathrm{I}_{2}(\mathrm{~g})+\mathrm{Cl}_{2}(\mathrm{~g}) ; \mathrm{K}_{\mathrm{C}}=0.14$
Solution. The given reaction is:
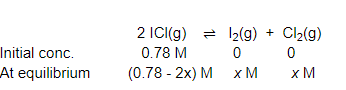
Now, we can write,
$\frac{\left[\mathrm{I}_{2}\right]\left[\mathrm{Cl}_{2}\right]}{[\mathrm{ICl}]^{2}}=K_{\mathrm{C}}$
$\Rightarrow \frac{x \times x}{(0.78-2 x)^{2}}=0.14$
$\Rightarrow \frac{x^{2}}{(0.78-2 x)^{2}}=0.14$
$\Rightarrow \frac{x}{0.78-2 x}=0.374$
$\Rightarrow x=0.292-0.748 x$
$\Rightarrow 1.748 x=0.292$
$\Rightarrow x=0.167$
Hence, at equilibrium,
$[\mathrm{ICl}]=\left[\mathrm{I}_{2}\right]=0.167 \mathrm{M}$
$[\mathrm{ICl}]=(0.78-2 \times 0.167) \mathrm{M}$
$=0.446 \mathrm{M}$
Question 17: $K_{\mathrm{p}}=0.04 \mathrm{~atm}$ at $899 \mathrm{~K}$ for the equilibrium shown below. What is the equilibrium concentration of $\mathrm{C}_{2} \mathrm{H}_{6}$ when it is placed in a flask at $4.0$ atm pressure and allowed to come to equilibrium?
Solution. Let $p$ be the pressure exerted by ethene and hydrogen gas (each) at equilibrium.
Now, according to the reaction,
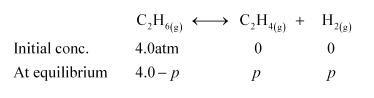
We can write,
$\frac{p_{\mathrm{C}_{2} \mathrm{H}_{4}} \times p_{\mathrm{H}_{2}}}{p_{\mathrm{C}_{2} \mathrm{H}_{6}}}=K_{p}$
$\Rightarrow \frac{p \times p}{4.0-p}=0.04$
$\Rightarrow p^{2}+0.16-0.04 p$
$\Rightarrow p^{2}+0.04 p-0.16=0$
Now, $p=\frac{-0.04 \pm \sqrt{(0.04)^{2}-4 \times 1 \times(-0.16)}}{2 \times 1}$
$=\frac{-0.04 \pm 0.80}{2}$
$=\frac{0.76}{2} \quad$ (Taking positive value) $=\frac{0.76}{2} \quad$ (Taking positive value)
$=0.38$
Hence, at equilibrium,
$\left[\mathrm{C}_{2} \mathrm{H}_{6}\right]-4-p=4-0.38$
$=3.62 \mathrm{~atm}$
Question 18: Ethyl acetate is formed by the reaction between ethanol and acetic acid and the equilibrium is represented as:
$\mathrm{CH}_{3} \mathrm{COOH}(\mathrm{l})+\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}$ ( 1$)$
$\longleftrightarrow \mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}$ (I) $+\mathrm{H}_{2} \mathrm{O}$ (I)
(i) Write the concentration ratio (reaction quotient), $Q \mathrm{c}$, for this reaction (note: water is not in excess and is not a solvent in this reaction)
(ii) At $293 \mathrm{~K}$, if one starts with $1.00 \mathrm{~mol}$ of acetic acid and $0.18 \mathrm{~mol}$ of ethanol, there is $0.171 \mathrm{~mol}$ of ethyl acetate in the final equilibrium mixture. Calculate the equilibrium constant.
(iii) Starting with $0.5 \mathrm{~mol}$ of ethanol and $1.0 \mathrm{~mol}$ of acetic acid and maintaining it at $293 \mathrm{~K}, 0.214$ mol of ethyl acetate is found after sometime. Has equilibrium been reached?
Solution. (i) Reaction quotient, $Q_{c}$
$=\frac{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}\right]}$
(ii) Let the volume of the reaction mixture be $V$. Also, here we will consider that water is a solvent and is present in excess.
The given reaction is:
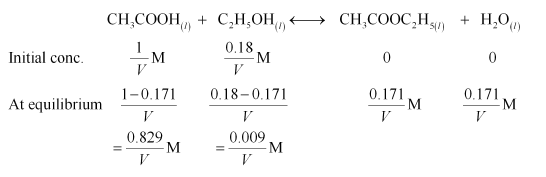
Therefore, equilibrium constant for the given reaction is:
$K_{\mathrm{C}}=\frac{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}\right]}$
$=\frac{\frac{0.171}{V} \times \frac{0.171}{V}}{\frac{0.829}{V} \times \frac{0.009}{V}}=3.919$
$=3.92$ (approximately)
(iii) Let the volume of the reaction mixture be $V$.
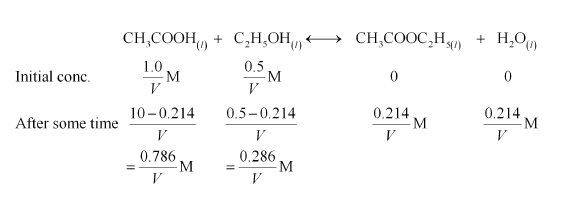
Therefore, the reaction quotient is,
$Q_{\mathrm{C}}=\frac{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}\right]}$
$=\frac{\frac{0.214}{V} \times \frac{0.214}{V}}{\frac{0.786}{V} \times \frac{0.286}{V}}$
$=0.2037$
$=0204$ (approximately)
Since $Q_{\mathrm{C}}
Question 19: A sample of pure $\mathrm{PCl}_{5}$ was introduced into an evacuated vessel at $473 \mathrm{~K}$. After equilibrium was attained, concentration of $\mathrm{PCl}_{5}$ was found to
be $0.5 \times 10^{-1} \mathrm{~mol} \mathrm{~L}^{-1}$. If value of $K_{c}$ is $8.3 \times 10^{-3}$, what are the concentrations of $\mathrm{PCl}_{3}$ and $\mathrm{Cl}_{2}$ at equilibrium?
$\mathrm{PCl}_{5}(\mathrm{~g}) \longleftrightarrow \mathrm{PCl}_{3}(\mathrm{~g})+\mathrm{Cl}_{2}(\mathrm{~g})$
Solution. Let the concentrations of both $\mathrm{PCl}_{3}$ and $\mathrm{Cl}_{2}$ at equilibrium be $x \mathrm{moll}^{-1}$. The given reaction is:

It is given that the value of equilibrium constant, $K_{\mathrm{C}}$ is $8.3 \times 10^{-3}$.
Now we can write the expression for equilibrium as:
$\frac{\left[\mathrm{PCl}_{2}\right]\left[\mathrm{Cl}_{2}\right]}{\left[\mathrm{PCl}_{5}\right]}=K_{\mathrm{C}}$
$\Rightarrow \frac{x \times x}{0.5 \times 10^{-1}}=8.3 \times 10^{-3}$
$\Rightarrow x^{2}=4.15 \times 10^{-4}$
$\Rightarrow x=2.04 \times 10^{-2}$
$=0.0204$
$=0.02$ (approximately)
Therefore, at equilibrium,
$\left[\mathrm{PCl}_{3}\right]=\left[\mathrm{Cl}_{2}\right]=0.02 \mathrm{~mol} \mathrm{~L}^{-1} .$
Question 20: One of the reactions that takes place in producing steel from iron ore is the reduction of iron (II) oxide by carbon monoxide to give iron metal and $\mathrm{CO}_{2}$
$\mathrm{FeO}(\mathrm{s})+\mathrm{CO}(\mathrm{g}) \longleftrightarrow \mathrm{Fe}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g})$
$K_{p}=0.265$ at $1050 \mathrm{~K}$
What are the equilibrium partial pressures of $\mathrm{CO}$ and $\mathrm{CO}_{2}$ at $1050 \mathrm{~K}$ if the initial partial pressures are: $p_{\mathrm{co}}=1.4 \mathrm{~atm}$ and $p_{\mathrm{CO}_{2}}=0.80 \mathrm{~atm} ?$
Solution. For the given reaction,
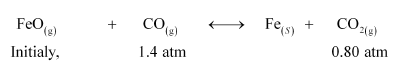
$Q_{\mathrm{P}}=\frac{p_{\mathrm{CO}_{2}}}{p_{\mathrm{CO}}}$
$=\frac{0.80}{1.4}$
$=0.571$
It is given that $K_{\mathrm{p}}=0.265$.
Since $Q_{\mathrm{p}}>K_{\mathrm{p}}$, the reaction will proceed in the backward direction.
Therefore, we can say that the pressure of CO will increase while the pressure of $\mathrm{CO}_{2}$ will decrease.
Now, let the increase in pressure of $\mathrm{CO}=$ decrease in pressure of $\mathrm{CO}_{2}$ be $p$
Then, we can write,
$K_{\mathrm{P}}=\frac{p_{\mathrm{CO}_{2}}}{p_{\mathrm{CO}}}$
$\Rightarrow 0.265=\frac{0.80-p}{1.4+p}$
$\Rightarrow 0.371+0.265 p=0.80-p$
$\Rightarrow 1.265 p=0.429$
$\Rightarrow p=0.339 \mathrm{~atm}$
Therefore, equilibrium partial of $\mathrm{CO}_{2}, p_{\mathrm{co}}$
$=0.80-0.339=0.461 \mathrm{~atm}$
And, equilibrium partial pressure of $\mathrm{CO}, p_{\mathrm{co}}$
$=1.4+0.339=1.739 \mathrm{~atm} .$
Question 21: Equilibrium constant, $K_{c}$ for the reaction
$\mathrm{N}_{2}(\mathrm{~g})+3 \mathrm{H}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{NH}_{3}(\mathrm{~g})$ at $500 \mathrm{~K}$ is $0.061$
At a particular time, the analysis shows that composition of the reaction mixture is $3.0 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~N}_{2}, 2.0 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{H}_{2}$ and $0.5 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{NH}_{3}$. Is the reaction at equilibrium? If not in which direction does the reaction tend to proceed to reach equilibrium?
Solution. The given reaction is:
$\mathrm{N}_{2(\mathrm{~g})}+3 \mathrm{H}_{2(\mathrm{~g})} \longleftrightarrow \quad 2 \mathrm{NH}_{3(\mathrm{~g})}$
At a particular time: $3.0 \mathrm{~mol} \mathrm{~L}^{-1} \quad 2.0 \mathrm{~mol} \mathrm{~L}^{-1}$ $0.5 \mathrm{~mol} \mathrm{~L}^{-1}$
Now, we know that,
$Q_{\mathrm{C}}=\frac{\left[\mathrm{NH}_{3}\right]^{2}}{\left[\mathrm{~N}_{2}\right]\left[\mathrm{H}_{2}\right]^{3}}$
$=\frac{(0.5)^{2}}{(3.0)(2.0)^{3}}$
$=0.0104$
It is given that $K_{\mathrm{C}}=0.061$.
Since $Q_{\mathrm{C}} \neq K_{\mathrm{c}}$, the reaction is not at equilibrium.
Since $Q_{\mathrm{C}}
Question 22: Bromine monochloride, $\mathrm{BrCl}$ decomposes into bromine and chlorine and reaches the equilibrium:
$2 \mathrm{BrCl}(\mathrm{g}) \longleftrightarrow \mathrm{Br}_{2}(\mathrm{~g})+\mathrm{Cl}_{2}(\mathrm{~g})$
for which $K_{c}=32$ at $500 \mathrm{~K}$. If initially pure $\mathrm{BrCl}$ is present at a concentration of $3.3 \times 10^{-3} \mathrm{molL}^{-1}$, what is its molar concentration in the mixture at equilibrium?
Solution. Let the amount of bromine and chlorine formed at equilibrium be $x$. The given reaction is:

Now, we can write,
$\frac{\left[\mathrm{Br}_{2}\right]\left[\mathrm{Cl}_{2}\right]}{[\mathrm{BrCl}]^{2}}=K_{\mathrm{C}}$
$\Rightarrow \frac{x \times x}{\left(3.3 \times 10^{-3}-2 x\right)^{2}}=32$
$\Rightarrow \frac{x}{3.3 \times 10^{-3}-2 x}=5.66$
$\Rightarrow x=18.678 \times 10^{-3}-11.32 x$
$\Rightarrow 12.32 x=18.678 \times 10^{-3}$
$\Rightarrow x=1.5 \times 10^{-3}$
Therefore, at equilibrium,
$[\mathrm{BrCl}]=3.3 \times 10^{-3}-\left(2 \times 1.5 \times 10^{-3}\right)$
$=3.3 \times 10^{-3}-3.0 \times 10^{-3}$
$=0.3 \times 10^{-3}$
$=3.0 \times 10^{-4} \mathrm{molL}^{-1}$
Question 23: At $1127 \mathrm{~K}$ and 1 atm pressure, a gaseous mixture of $\mathrm{CO}$ and $\mathrm{CO}_{2}$ in equilibrium with solid carbon has $90.55 \%$ CO by mass
$\mathrm{C}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{CO}(\mathrm{g})$
Calculate $K_{c}$ for this reaction at the above temperature.
Solution. Let the total mass of the gaseous mixture be $100 \mathrm{~g}$.
Mass of $\mathrm{CO}=90.55 \mathrm{~g}$
And, mass of $\mathrm{CO}_{2}=(100-90.55)=9.45 \mathrm{~g}$
Now, number of moles of $\mathrm{CO}$
$n_{\mathrm{CO}}=\frac{90.55}{28}=3.234 \mathrm{~mol}$
Number of moles of $\mathrm{CO}_{2}$
$n_{\mathrm{CO}_{2}}=\frac{9.45}{44}=0.215 \mathrm{~mol}$
Partial pressure of $\mathrm{CO}$
$p_{\mathrm{CO}}=\frac{n_{\mathrm{CO}}}{n_{\mathrm{CO}}+n_{\mathrm{CO}_{2}}} \times p_{\text {total }}$
$=\frac{3.234}{3.234+0.215} \times 1$
$=0.938 \mathrm{~atm}$
Partial pressure of $\mathrm{CO}_{2}$
$p_{\mathrm{CO}_{2}}=\frac{n_{\mathrm{CO}_{2}}}{n_{\mathrm{CO}}+n_{\mathrm{CO}_{2}}} \times p_{\text {tocal }}$
$=\frac{0.215}{3.234+0.215} \times 1$
$=0.062 \mathrm{~atm}$
Therefore, $K_{\mathrm{p}}=\frac{[\mathrm{CO}]^{2}}{\left[\mathrm{CO}_{2}\right]}$
$=\frac{(0.938)^{2}}{0.062}$
$=14.19$
For the given reaction,
$\Delta n=2-1=1$
We know that,
$K_{\mathrm{P}}=K_{\mathrm{C}}(R T)^{\mathrm{N}}$
$\Rightarrow 14.19=K_{\mathrm{C}}(0.082 \times 1127)^{\prime}$
$\Rightarrow K_{\mathrm{C}}=\frac{14.19}{0.082 \times 1127}$
$=0.154($ approximately $)$
Question 24: Calculate
a) $\Delta G^{\circ}$ and $b$ ) the equilibrium constant for the formation of $\mathrm{NO}_{2}$ from $\mathrm{NO}$ and $\mathrm{O}_{2}$ at $298 \mathrm{~K}$
$\mathrm{NO}(\mathrm{g})+1 / 2 \mathrm{O}_{2}(\mathrm{~g}) \longleftrightarrow \mathrm{NO}_{2}(\mathrm{~g})$
where $\Delta_{f} G^{\circ}\left(\mathrm{NO}_{2}\right)=52.0 \mathrm{~kJ} / \mathrm{mol}$
$\Delta_{f} G^{\circ}(\mathrm{NO})=87.0 \mathrm{~kJ} / \mathrm{mol}$
$\Delta_{f} \mathrm{G}^{\circ}\left(\mathrm{O}_{2}\right)=0 \mathrm{~kJ} / \mathrm{mol}$
Solution. (a) For the given reaction,
$\Delta G^{\circ}=\Delta G^{\circ}($ Products $)-\Delta G^{\circ}($ Reactants $)$
$\Delta G^{\circ}=52.0-\{87.0+0\}$
$=-35.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$
(b) We know that,
$\Delta G^{\circ}=R T \log K_{c}$
$\Delta G^{\circ}=2.303 \mathrm{RT} \log K_{c}$
$K_{c}=\frac{-35.0 \times 10^{-3}}{-2.303 \times 8.314 \times 298}$
$=6.134$
$\therefore K_{c}=$ antilog $(6.134)$
$=1.36 \times 10^{6}$
Hence, the equilibrium constant for the given reaction $K_{c}$ is $1.36 \times 10^{6}$
Question $25$ : Does the number of moles of reaction products increase, decrease or remain same when each of the following equilibria is subjected to a decrease in pressure by increasing the volume?
(a) $\mathrm{PCl}_{5}(\mathrm{~g}) \longleftrightarrow \mathrm{PCl}_{3}(\mathrm{~g})+\mathrm{Cl}_{2}$ (g)
(b) $\mathrm{CaO}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g}) \longleftrightarrow \mathrm{CaCO}_{3}(\mathrm{~s})$
(c) $3 \mathrm{Fe}(\mathrm{s})+4 \mathrm{H}_{2} \mathrm{O}(\mathrm{g}) \longleftrightarrow \mathrm{Fe}_{3} \mathrm{O}_{4}(\mathrm{~s})+4 \mathrm{H}_{2}(\mathrm{~g})$
Solution. (a) The number of moles of reaction products will increase. According to Le Chatelier's principle, if pressure is decreased, then the equilibrium shifts in the direction in which the number of moles of gases is more. In the given reaction, the number of moles of gaseous products is more than that of gaseous reactants. Thus, the reaction will proceed in the forward direction. As a result, the number of moles of reaction products will increase.
(b) The number of moles of reaction products will decrease.
(c) The number of moles of reaction products remains the same.
Question 26: Which of the following reactions will get affected by increasing the pressure?
Also, mention whether change will cause the reaction to go into forward or backward direction.
(i) $\mathrm{COCl}_{2}(\mathrm{~g}) \longleftrightarrow \mathrm{CO}(\mathrm{g})+\mathrm{Cl}_{2}(\mathrm{~g})$
(ii) $\mathrm{CH}_{4}(\mathrm{~g})+2 \mathrm{~S}_{2}$$(\mathrm{g}) \longleftrightarrow \mathrm{CS}_{2}(\mathrm{~g})+2 \mathrm{H}_{2} \mathrm{~S}(\mathrm{~g})$
(iii) $\mathrm{CO}_{2}(\mathrm{~g})+\mathrm{C}(\mathrm{s}) \longleftrightarrow 2 \mathrm{CO}(\mathrm{g})$
(iv) $2 \mathrm{H}_{2}(\mathrm{~g})+\mathrm{CO}(\mathrm{g}) \longleftrightarrow \mathrm{CH}_{3} \mathrm{OH}(\mathrm{g})$
(v) $\mathrm{CaCO}_{3}(\mathrm{~s}) \longleftrightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g})$
(vi) $4 \mathrm{NH}_{3}(\mathrm{~g})+5 \mathrm{O}_{2}(\mathrm{~g}) \longleftrightarrow 4 \mathrm{NO}(\mathrm{g})+6 \mathrm{H}_{2} \mathrm{O}(\mathrm{g})$
Solution. The reactions given in (i), (iii), (iv), (v), and (vi) will get affected by increasing the pressure.
The reaction given in (iv) will proceed in the forward direction because the number of moles of gaseous reactants is more than that of gaseous products.
The reactions given in (i), (iii), (v), and (vi) will shift in the backward direction because the number of moles of gaseous reactants is less than that of gaseous products.
Question 27: The equilibrium constant for the following reaction is $1.6 \times 10^{5}$ at $1024 \mathrm{~K}$.
$\mathrm{H}_{2}(\mathrm{~g})+\mathrm{Br}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{HBr}(\mathrm{g})$strong>
Find the equilibrium pressure of all gases if $10.0$ bar of $\mathrm{HBr}$ is introduced into a sealed container at $1024 \mathrm{~K}$.
Solution. Given.
$K_{p}$ for the reaction i.e., $\mathrm{H}_{2(\mathrm{~g})}$
$+\mathrm{Br}_{2(g)} \longleftrightarrow 2 \mathrm{HBr}_{(\mathrm{g})}$ is $1.6 \times 10^{5}$
Therefore, for the reaction $2 \mathrm{HBr}_{(\mathrm{g})} \longleftrightarrow \mathrm{H}_{2(\mathrm{~g})}$
$+\mathrm{Br}_{2(\mathrm{~g})}$, the equilibrium constant will be,
$K_{\mathrm{p}}^{\prime}=\frac{1}{K_{\mathrm{P}}}$
$=\frac{1}{1.6 \times 10^{5}}$
$=6.25 \times 10^{-6}$
Now, let $p$ be the pressure of both $\mathrm{H}_{2}$ and $\mathrm{Br}_{2}$ at equilibrium.

Now, we can write,
$\frac{p_{\mathrm{HB}_{1}} \times p_{2}^{\times}}{p_{\mathrm{HBr}}^{2}}=K_{\mathrm{P}}^{\prime}$
$\frac{p \times p}{(10-2 p)^{2}}=6.25 \times 10^{-6}$
$\frac{p}{10-2 p}=2.5 \times 10^{-3}$
$p=2.5 \times 10^{-2}-\left(5.0 \times 10^{-3}\right) p$
$p+\left(5.0 \times 10^{-3}\right) p=2.5 \times 10^{-2}$
$\left(1005 \times 10^{-3}\right) p=2.5 \times 10^{-2}$
$p=2.49 \times 10^{-2}$ bar $=2.5 \times 10^{-2}$ bar (approximately)
Therefore, at equilibrium,
$\left[\mathrm{H}_{2}\right]=\left[\mathrm{Br}_{2}\right]=2.49 \times 10^{-2} \mathrm{bar}$
$[\mathrm{HBr}]=10-2 \times\left(2.49 \times 10^{-2}\right) \mathrm{bar}$
$=9.95 \mathrm{bar}=10 \mathrm{bar}($ approximately $)$
Question $28:$ Dihydrogen gas is obtained from natural gas by partial oxidation with steam as per following endothermic reaction:
$\mathrm{CH}_{4}(\mathrm{~g})+\mathrm{H}_{2} \mathrm{O}(\mathrm{g}) \longleftrightarrow \mathrm{CO}(\mathrm{g})+3 \mathrm{H}_{2}(\mathrm{~g})$
(a) Write as expression for $K_{p}$ for the above reaction.
(b) How will the values of $K_{p}$ and composition of equilibrium mixture be affected by
(i) Increasing the pressure
(ii) Increasing the temperature
(iii) Using a catalyst?
Solution. (a) For the given reaction,
$K_{P}=\frac{p_{\mathrm{CO}} \times p_{\mathrm{H}_{2}}^{3}}{p_{\mathrm{CH}_{4}} \times p_{\mathrm{H}_{2} \mathrm{O}}}$
(b) (i) According to Le Chatelier's principle, the equilibrium will shift in the backward direction.
(ii) According to Le Chatelier's principle, as the reaction is endothermic, the equilibrium will shift in the forward direction.
(iii) The equilibrium of the reaction is not affected by the presence of a catalyst. A catalyst only increases the rate of a reaction. Thus, equilibrium will be attained quickly.
Question 29: Describe the effect of:
a) Addition of $\mathrm{H}_{2}$
b) Addition of $\mathrm{CH}_{3} \mathrm{OH}$
c) Removal of $\mathrm{CO}$
d) Removal of $\mathrm{CH}_{3} \mathrm{OH}$
on the equilibrium of the reaction:
$2 \mathrm{H}_{2}(\mathrm{~g})+\mathrm{CO}(\mathrm{g}) \longleftrightarrow \mathrm{CH}_{3} \mathrm{OH}(\mathrm{g})$
Solution. (a) According to Le Chatelier's principle, on addition of $\mathrm{H}_{2}$, the equilibrium of the given reaction will shift in the forward direction.
(b) On addition of $\mathrm{CH}_{3} \mathrm{OH}$, the equilibrium will shift in the backward direction.
(c) On removing CO, the equilibrium will shift in the backward direction.
(d) On removing $\mathrm{CH}_{3} \mathrm{OH}$, the equilibrium will shift in the forward direction.
Question 30: At $473 \mathrm{~K}$, equilibrium constant $K_{c}$ for decomposition of phosphorus pentachloride, $\mathrm{PCl}_{5}$ is $8.3 \times 10^{-3}$. If decomposition is depicted as,
$\mathrm{PCl}_{5}(\mathrm{~g}) \longleftrightarrow \mathrm{PCl}_{3}(\mathrm{~g})+\mathrm{Cl}_{2}(\mathrm{~g})$
(g) $\Delta_{r} H^{\circ}=124.0 \mathrm{kJmol}^{-1}$
a) Write an expression for $K_{c}$ for the reaction.
b) What is the value of $K_{c}$ for the reverse reaction at the same temperature?
c) What would be the effect on $K_{c}$ if (i) more $\mathrm{PCl}_{5}$ is added (ii) pressure is increased? (iii) The temperature is increased?
Solution. (a) $K_{c} \frac{\left[\mathrm{PCl}_{3(\mathrm{~g})}\right]\left[\mathrm{Cl}_{2(\mathrm{~g})}\right]}{\left[\mathrm{PCl}_{5(\mathrm{~g})}\right]}$
(b) Value of $K_{c}$ for the reverse reaction at the same temperature is:
$K_{c}^{\prime}=\frac{1}{K_{c}}$
$=\frac{1}{8.3 \times 10^{-3}}=1.2048 \times 10^{2}$
$=120-48$
(c) (i) $K_{c}$ would remain the same because in this case, the temperature remains the same.
(ii) $K_{c}$ is constant at constant temperature. Thus, in this case, $K_{c}$ would not change.
(iii) In an endothermic reaction, the value of $K_{c}$ increases with an increase in temperature. Since the given reaction in an endothermic reaction, the value of $K_{c}$ will increase if the temperature is increased.
Question 31: Dihydrogen gas used in Haber's process is produced by reacting methane from natural gas with high temperature steam. The first stage of two stage reaction involves the formation of $\mathrm{CO}$ and $\mathrm{H}_{2}$. In second stage, $\mathrm{CO}$ formed in first stage is reacted with more steam in water gas shift reaction,
$\mathrm{CO}(\mathrm{g})+\mathrm{H}_{2} \mathrm{O}(\mathrm{g}) \longleftrightarrow \mathrm{CO}_{2}(\mathrm{~g})+\mathrm{H}_{2}(\mathrm{~g})$
If a reaction vessel at $400^{\circ} \mathrm{C}$ is charged with an equimolar mixture of $\mathrm{CO}$ and steam such that $p_{\mathrm{CO}}=p_{\mathrm{H}_{2} \mathrm{O}}=4.0 \mathrm{bar}$, what will be the partial pressure of $\mathrm{H}_{2}$ at equilibrium? $\mathrm{Kp}=10.1$ at $400^{\circ} \mathrm{C}$
Solution. Let the partial pressure of both carbon dioxide and hydrogen gas be $p$. The given reaction is:
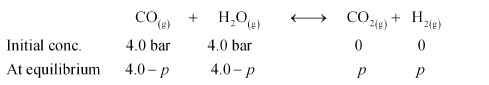
It is given that $K_{\mathrm{p}}=10.1$.
Now,
$\frac{p_{\mathrm{CO}_{2}} \times p_{\mathrm{H}_{2}}}{p_{\mathrm{CO}+} \times \mathrm{P}_{2}}=K_{\mathrm{P}}$
$\Rightarrow \frac{p \times p}{(4.0-p)(4.0-p)}=10.1$
$\Rightarrow \frac{p}{4.0-p}=3.178$
$\Rightarrow p=12.712-3.178 p$
$\Rightarrow 4.178 p=12.712$
$\Rightarrow p=3.04$
Hence, at equilibrium, the partial pressure of $\mathrm{H}_{2}$ will be $3.04$ bar.
Question $32$ : Predict which of the following reaction will have appreciable concentration of reactants and products:
a) $\mathrm{Cl}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{Cl}(\mathrm{g}) ; \quad K_{c}=5 \times 10^{-39}$
$K_{c}=3.7 \times 10^{8}$
b) $\mathrm{Cl}_{2}(\mathrm{~g})+2 \mathrm{NO}(\mathrm{g}) \longleftrightarrow 2 \mathrm{NOCl}(\mathrm{g})$;
$K_{c}=3.7 \times 10^{8}$
c) $\mathrm{Cl}_{2}(\mathrm{~g})+2 \mathrm{NO}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{NO}_{2} \mathrm{Cl}(\mathrm{g})$;
$K_{c}=1.8$
Solution. If the value of $K_{c}$ lies between $10^{-3}$ and $10^{3}$, a reaction has appreciable concentration of reactants and products. Thus, the reaction given in (c) will have appreciable concentration of reactants and products.
Question $33$ : The value of $K_{c}$ for the reaction
$3 \mathrm{O}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{O}_{3}(\mathrm{~g})$
is $2.0 \times 10^{-50}$ at $25^{\circ} \mathrm{C}$. If the equilibrium concentration of $\mathrm{O}_{2}$ in air at $25^{\circ} \mathrm{C}$ is $1.6 \times 10^{-2}$, what is the concentration of $\mathrm{O}_{3} ?$
Solution. The given reaction is:
$3 \mathrm{O}_{2(\mathrm{~g})} \longleftrightarrow 2 \mathrm{O}_{3(\mathrm{~g})}$
Then,
$K_{C}=\frac{\left[\mathrm{O}_{3(\mathrm{~g})}\right]^{2}}{\left[\mathrm{O}_{2(\mathrm{~g})}\right]^{3}}$
It is given that $K_{\mathrm{C}}=2.0 \times 10^{-50}$
and $\left[\mathrm{O}_{2(\mathrm{~g})}\right]=1.6 \times 10^{-2}$.
Then, we have,
$2.0 \times 10^{-50}=\frac{\left[\mathrm{O}_{3(\mathrm{~g})}\right]^{2}}{\left[1.6 \times 10^{-2}\right]^{3}}$
$\Rightarrow\left[\mathrm{O}_{3(\mathrm{~g})}\right]^{2}=2.0 \times 10^{-50} \times\left(1.6 \times 10^{-2}\right)^{3}$
$\Rightarrow\left[\mathrm{O}_{3(\mathrm{~g})}\right]^{2}=8.192 \times 10^{-56}$
$\Rightarrow\left[\mathrm{O}_{3(\mathrm{~g})}\right]=2.86 \times 10^{-28} \mathrm{M}$
Hence, the concentration of $\mathrm{O}_{3}$ is $2.86 \times 10^{-28} \mathrm{M}$.
Question 34: The reaction, $\mathrm{CO}(\mathrm{g})+3 \mathrm{H}_{2}(\mathrm{~g}) \longleftrightarrow \mathrm{CH}_{4}(\mathrm{~g})+\mathrm{H}_{2} \mathrm{O}(\mathrm{g})$ is at equilibrium at $1300 \mathrm{~K}$ in a $1 \mathrm{~L}$ flask. It also contain $0.30 \mathrm{~mol}$ of $\mathrm{CO}, 0.10 \mathrm{~mol}$ of $\mathrm{H}_{2}$ and $0.02 \mathrm{~mol}$ of $\mathrm{H}_{2} \mathrm{O}$ and an unknown amount of $\mathrm{CH}_{4}$ in the flask. Determine the concentration of $\mathrm{CH}_{4}$ in the mixture. The equilibrium constant, $K_{c}$ for the reaction at the given temperature is $3.90$.
Solution. Let the concentration of methane at equilibrium be $x$.

It is given that $K_{c}=3.90$.
Therefore,
$\frac{\left[\mathrm{CH}_{4(\mathrm{~g})}\right]\left[\mathrm{H}_{2} \mathrm{O}_{(\mathrm{g})}\right]}{\left[\mathrm{CO}_{(\mathrm{g})}\right]\left[\mathrm{H}_{2(\mathrm{~g})}\right]^{3}}=K_{c}$
$\Rightarrow \frac{x \times 0.02}{0.3 \times(0.1)^{3}}=3.90$
$\Rightarrow x=\frac{3.90 \times 0.3 \times(0.1)^{3}}{0.02}$
$=\frac{0.00117}{0.02}$
$=0.0585 \mathrm{M}$
$=5.85 \times 10^{-2} \mathrm{M}$
Hence, the concentration of $\mathrm{CH}_{4}$ at equilibrium is $5.85 \times 10^{-2} \mathrm{M}$.
Question 35: What is meant by the conjugate acid-base pair? Find the conjugate acid/base for the following species:
$\mathrm{HNO}_{2}, \mathrm{CN}^{-}, \mathrm{HClO}_{4}, \mathrm{~F}^{-}, \mathrm{OH}^{-}, \mathrm{CO}_{3}^{2-}$, and $\mathrm{S}^{-}$
Solution. A conjugate acid-base pair is a pair that differs only by one proton.
The conjugate acid-base for the given species is mentioned in the table below.

Question 36: Which of the followings are Lewis acids? $\mathrm{H}_{2} \mathrm{O}, \mathrm{BF}_{3}, \mathrm{H}^{+}$, and $\mathrm{NH}_{4}^{+}$
Solution. Lewis acids are those acids which can accept a pair of electrons. For example, $\mathrm{BF}_{3}, \mathrm{H}^{+}$, and $\mathrm{NH}_{4}^{+}$ are Lewis acids.
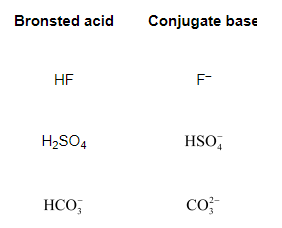
Question 37: What will be the conjugate bases for the Brönsted acids: $\mathrm{HF}_{1} \mathrm{H}_{2} \mathrm{SO}_{4}$ and $\mathrm{HCO}_{3}$ ?
Solution. The table below lists the conjugate bases for the given Bronsted acids.
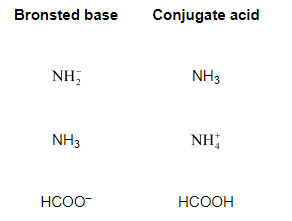
Question 38: Write the conjugate acids for the following Brönsted bases: $\mathrm{NH}_{2}^{-}, \mathrm{NH}_{3}$ and $\mathrm{HCOO}^{-}$.
Solution. The table below lists the conjugate acids for the given Bronsted bases.
Question $39:$ The species: $\mathrm{H}_{2} \mathrm{O}, \mathrm{HCO}_{3}^{-}, \mathrm{HSO}_{4}^{-}$, and $\mathrm{NH}_{3}$ can act both as Brönsted acids and bases. For each case give the corresponding conjugate acid and base.
Solution. The table below lists the conjugate acids and conjugate bases for the given species.

Question 40: Classify the following species into Lewis acids and Lewis bases and show how these act as Lewis acid/base: (a) $\mathrm{OH}^{-}$ (b) $\mathrm{F}^{-}$ (c) $\mathrm{H}^{+}$ (d) $\mathrm{BCl}_{3}$.
Solution. (a) $\mathrm{OH}^{-}$ is a Lewis base since it can donate its lone pair of electrons.
(b) $\mathrm{F}^{-}$ is a Lewis base since it can donate a pair of electrons.
(c) $\mathrm{H}^{+}$ is a Lewis acid since it can accept a pair of electrons.
(d) $\mathrm{BCl}_{3}$ is a Lewis acid since it can accept a pair of electrons.
Question 41: The concentration of hydrogen ion in a sample of soft drink is $3.8 \times 10^{-3} \mathrm{M}$. what is its $\mathrm{pH}$ ?
Solution. Given,
$\left[\mathrm{H}^{+}\right]=3.8 \times 10^{-3} \mathrm{M}$
$\therefore \mathrm{pH}$ value of soft drink
$=-\log \left[\mathrm{H}^{+}\right]$
$=-\log \left(3.8 \times 10^{-3}\right)$
$=-\log 3.8-\log 10^{-3}$
$=-\log 3.8+3$
$=-0.58+3$
$=2.42$
Question $42$ : The $\mathrm{pH}$ of a sample of vinegar is $3.76 .$ Calculate the concentration of hydrogen ion in it.
Solution. Given,
$\mathrm{pH}=3.76$
It is known that,
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$\Rightarrow \log \left[\mathrm{H}^{+}\right]=-\mathrm{pH}$
$\Rightarrow\left[\mathrm{H}^{+}\right]=\operatorname{antilog}(-\mathrm{pH})$
$=\operatorname{antil} \operatorname{og}(-3.76)$
$=1.74 \times 10^{-4} \mathrm{M}$
Hence, the concentration of hydrogen ion in the given sample of vinegar is $1.74 \times 10^{-4} \mathrm{M}$.
Question $43:$ mThe ionization constant of HF, HCOOH and HCN at $298 \mathrm{~K}$ are
$6.8 \times 10^{-4}, 1.8 \times 10^{-4}$ and $4.8 \times 10^{-9}$ respectively. Calculate the ionization constants of the corresponding conjugate base
Solution. It is known that,
$K_{b}=\frac{K_{w}}{K_{a}}$
Given,
$K_{a}$ of $\mathrm{HF}=6.8 \times 10^{-4}$
Hence, $K_{b}$ of its conjugate base $\mathrm{F}^{-}$
$=\frac{K_{w}}{K_{a}}$
$=\frac{10^{-14}}{6.8 \times 10^{-4}}$
$=1.5 \times 10^{-11}$
Given,
$K_{a}$ of $\mathrm{HCOOH}=1.8 \times 10^{-4}$
Hence, $K_{b}$ of its conjugate base $\mathrm{HCOO}^{-}$
$=\frac{K_{w}}{K_{a}}$
$=\frac{10^{-14}}{1.8 \times 10^{-4}}$
$=5.6 \times 10^{-11}$
Given,
$K_{a}$ of $\mathrm{HCN}=4.8 \times 10^{-9}$
Hence, $K_{b}$ of its conjugate base $\mathrm{CN}^{-}$
$=\frac{K_{w}}{K_{a}}$
$=\frac{10^{-14}}{4.8 \times 10^{-9}}$
$=2.08 \times 10^{-6}$’
Question $44$ : The ionization constant of phenol is $1.0 \times 10^{-10} .$ What is the concentration of phenolate ion in $0.05 \mathrm{M}$ solution of phenol? What will be its degree of ionization if the solution is also $0.01 \mathrm{M}$ in sodium phenolate?
Solution. lonization of phenol:
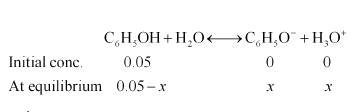
$K_{a}=\frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{OH}\right]}$
$K_{\sigma}=\frac{x \times x}{0.05-x}$
As the value of the tonization constant is very less, $x$ will be very small. Thus,
we can ignore $x$ in the denominator.
$\therefore x=\sqrt{1 \times 10^{-10} \times 0.05}$
$=\sqrt{5 \times 10^{-12}}$
$=2.2 \times 10^{-6} \mathrm{M}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]$
Since $\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]$
Now, let $\propto$ be the degree of ionization of phenol in the presence of $0.01 \mathrm{M} \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{ONa}$.
$\begin{array}{rr} & \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{ONa} \longrightarrow \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}+\mathrm{Na}^{+} \\ \text {Conc. } & 0.01\end{array}$
Also,
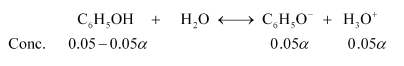
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{OH}\right]=0.05-0.05 \alpha ; 0.05 \mathrm{M}$
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]=0.01+0.05 \alpha ; 0.01 \mathrm{M}$
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=0.05 \alpha$
$K_{a}=\frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{OH}\right]}$
$K_{a}=\frac{(0.01)(0.05 \alpha)}{0.05}$
$1.0 \times 10^{-10}=.01 \alpha$
$\alpha=1 \times 10^{-8}$
Question $45$ : also? If the second dissociation constant of $\mathrm{H}_{2} \mathrm{~S}$ is $1.2 \times 10^{-13}$, calculate the concentration of $\mathrm{S}^{2-}$ under both conditions.
Solution. (i) To calculate the concentration of $\mathrm{HS}^{-}$ ion:
Case I (in the absence of $\mathrm{HCl}$ ):
Let the concentration of $\mathrm{HS}^{-}$ be $\times \mathrm{M}$.
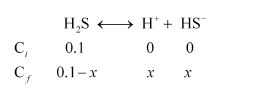
Then, $K_{a_{1}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{HS}^{-}\right]}{\left[\mathrm{H}_{2} \mathrm{~S}\right]}$
$9.1 \times 10^{-8}=\frac{(x)(x)}{0.1-x}$
$\left(9.1 \times 10^{-8}\right)(0.1-x)=x^{2}$
Taking $0.1-x \mathrm{M} ; 0.1 \mathrm{M}$, we have $\left(9.1 \times 10^{-8}\right)(0.1)=x^{2}$.
$9.1 \times 10^{-9}=x^{2}$
$x=\sqrt{9.1 \times 10^{-9}}$
$=9.54 \times 10^{-5} \mathrm{M}$
$=9.54 \times 10^{-5} \mathrm{M}$
$\Rightarrow\left[\mathrm{HS}^{-}\right]=9.54 \times 10^{-5} \mathrm{M}$
Case II (in the presence of $\mathrm{HCl}$ ):
In the presence of $0.1 \mathrm{M}$ of $\mathrm{HCl}$, let $\left[\mathrm{HS}^{-}\right]$ be $y \mathrm{M}$.
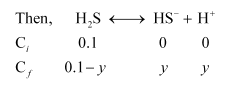

Now, $K_{o_{1}}=\frac{\left[\mathrm{HS}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{H}_{2} \mathrm{~S}\right]}$
$K_{a_{1}}=\frac{[y](0.1+y)}{(0.1-y)}$
$9.1 \times 10^{-8}=\frac{y \times 0.1}{0.1}$
$(\because 0.1-y ; 0.1 \mathrm{M})$
$($ and $0.1+y ; 0.1 \mathrm{M})$
$9.1 \times 10^{-8}=y$
$\Rightarrow\left[\mathrm{HS}^{-}\right]=9.1 \times 10^{-8}$
(ii) To calculate the concentration of $\left[\mathrm{S}^{2-}\right]$
Case I (in the absence of $0.1 \mathrm{M} \mathrm{HCl}$ ):
$\mathrm{HS}^{-} \longleftrightarrow \mathrm{H}^{+}+\mathrm{S}^{2-}$
$\left[\mathrm{HS}^{-}\right]=9.54 \times 10^{-5} \mathrm{M}$ (From first ionization, case I)
Let $\left[\mathrm{S}^{2-}\right]$ be $X$.
Also, $\left[\mathrm{H}^{+}\right]=9.54 \times 10^{-5} \mathrm{M}$ (From first ionization, case I)
$K_{a_{2}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]}$
$K_{a_{2}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]}$
$K_{a_{2}}=\frac{\left(9.54 \times 10^{-5}\right)(X)}{9.54 \times 10^{-5}}$
$1.2 \times 10^{-13}=X=\left[\mathrm{S}^{2-}\right]$
Case II (in the presence of $0.1 \mathrm{M} \mathrm{HCl}$ ):
Again, let the concentration of $\mathrm{HS}^{-}$ be $X^{\prime} \mathrm{M}$.
$\left[\mathrm{HS}^{-}\right]=9.1 \times 10^{-8} \mathrm{M}$ (From first ionization, case II)
$\left[\mathrm{H}^{+}\right]=0.1 \mathrm{M}$ (From $\mathrm{HCl}$, case II $)$
$\left[\mathrm{S}^{2-}\right]=X^{\prime}$
Then, $K_{a_{2}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]}$
$1.2 \times 10^{-13}=\frac{(0.1)\left(X^{\prime}\right)}{9.1 \times 10^{-8}}$
$10.92 \times 10^{-21}=0.1 X^{\prime}$
$\frac{10.92 \times 10^{-21}}{0.1}=X^{\prime}$
$X^{\prime}=\frac{1.092 \times 10^{-20}}{0.1}$
$=1.092 \times 10^{-19} \mathrm{M}$
$\Rightarrow K_{a_{1}}=1.74 \times 10^{-5}$
Question $46$ : The ionization constant of acetic acid is $1.74 \times 10^{-5}$. Calculate the degree of dissociation of acetic acid in its $0.05 \mathrm{M}$ solution. Calculate the concentration of acetate ion in the solution and its $\mathrm{pH}$.
Solution. Method 1
1) $\mathrm{CH}_{3} \mathrm{COOH} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}^{+} \quad K_{a}=1.74 \times 10^{-5}$
2) $\mathrm{H}_{2} \mathrm{O}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{OH}^{-} \quad K_{w}=1.0 \times 10^{-14}$
Since $K a \gg K_{w,}$ :
$\mathrm{CH}_{3} \mathrm{COOH}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}_{3} \mathrm{O}^{+}$

$K_{a}=\frac{(.05 \alpha)(.05 \alpha)}{(.05-0.05 \alpha)}$
$0.05 \alpha^{2}+1.74 \times 10^{-5} \alpha-1.74 \times 10^{-5}$
$D=b^{2}-4 a c$
$=\left(1.74 \times 10^{-5}\right)^{2}-4(.05)\left(1.74 \times 10^{-5}\right)$
$=3.02 \times 10^{-25}+.348 \times 10^{-5}$
$\alpha=\sqrt{\frac{K_{a}}{c}}$
$\alpha=\sqrt{\frac{1.74 \times 10^{-5}}{.05}}$
$=\sqrt{\frac{34.8 \times 10^{-5} \times 10}{10}}$
$=\sqrt{3.48 \times 10^{-6}}$
$=\mathrm{CH}_{3} \mathrm{COOH} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}^{+}$
$\alpha 1.86 \times 10^{-3}$
$\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]=0.05 \times 1.86 \times 10^{-3}$
$=\frac{0.93 \times 10^{-3}}{1000}$
$=.000093$
Method 2
Degree of dissociation,
$\alpha=\sqrt{\frac{K_{a}}{c}}$
$c=0.05 \mathrm{M}$
$K_{a}=1.74 \times 10^{-5}$
Then, $\alpha=\sqrt{\frac{1.74 \times 10^{-5}}{.05}}$
$\alpha=\sqrt{34.8 \times 10^{-5}}$
$\alpha=\sqrt{3.48} \times 10^{-4}$
$\alpha=1.8610^{-2}$
$\mathrm{CH}_{3} \mathrm{COOH} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}^{+}$
Thus, concentration of $\mathrm{CH}_{3} \mathrm{COO}-=\mathrm{c} . \mathrm{a}$
$=.05 \times 1.86 \times 10^{-2}$
$=.093 \times 10^{-2}$
$=.00093 \mathrm{M}$
Since $\left[\mathrm{oAc}^{-}\right]=\left[\mathrm{H}^{+}\right]$
$\left[\mathrm{H}^{+}\right]=.00093=.093 \times 10^{-2} .$
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$=-\log \left(.093 \times 10^{-2}\right)$
$\therefore \mathrm{pH}=3.03$
Hence, the concentration of acetate ion in the solution is $0.00093 \mathrm{M}$ and its $\mathrm{Ph}$ is $3.03$.
Question 47: It has been found that the $\mathrm{pH}$ of a $0.01 \mathrm{M}$ solution of an organic acid is $4.15 .$ Calculate the concentration of the anion, the ionization constant of the acid and its $\mathrm{pK}_{\mathrm{a}}$
Solution. Let the organic acid be $\mathrm{HA}$.
$\Rightarrow \mathrm{HA} \longleftrightarrow \mathrm{H}^{+}+\mathrm{A}^{-}$
Concentration of $\mathrm{HA}=0.01 \mathrm{M}$
$\mathrm{pH}=4.15$
$-\log \left[\mathrm{H}^{+}\right]=4.15$
$\left[\mathrm{H}^{+}\right]=7.08 \times 10^{-5}$
Now, $K_{a}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}$
$\left[\mathrm{H}^{+}\right]=\left[\mathrm{A}^{-}\right]=7.08 \times 10^{-5}$
$[\mathrm{HA}]=0.01$
Then,
$K_{a}=\frac{\left(7.08 \times 10^{-5}\right)\left(7.08 \times 10^{-5}\right)}{0.01}$
$K_{a}=5.01 \times 10^{-7}$
$K_{o}=5.01 \times 10^{-7}$
$=-\log \left(5.01 \times 10^{-7}\right)$
$p K_{a}=6.3001$
Question 48: Assuming complete dissociation, calculate the $\mathrm{pH}$ of the following solutions:
(a) $0.003 \mathrm{M} \mathrm{HCl}$
(b) $0.005 \mathrm{M} \mathrm{NaOH}$
(c) $0.002 \mathrm{M} \mathrm{HBr}$
(d) $0.002 \mathrm{M} \mathrm{KOH}$
Solution. (i) $0.003 \mathrm{MHCl}$ :
$\mathrm{H}_{2} \mathrm{O}+\mathrm{HCl} \longleftrightarrow \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{Cl}^{-}$
Since $\mathrm{HCl}$ is completely ionized,
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{HCl}]$
$\Rightarrow\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=0.003$
Now,
$\mathrm{pH}=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=-\log (.003)$
$=2.52$
Hence, the $\mathrm{pH}$ of the solution is $2.52 .$
(ii) $0.005 \mathrm{MNaOH}$ :
$\mathrm{NaOH}_{(a q)} \longleftrightarrow \mathrm{Na}_{(a q)}^{+}+\mathrm{HO}_{(a q)}^{-}$
$\left[\mathrm{HO}^{-}\right]=[\mathrm{NaOH}]$
$\Rightarrow\left[\mathrm{HO}^{-}\right]=.005$
$\mathrm{pOH}=-\log \left[\mathrm{HO}^{-}\right]=-\log (.005)$
$\mathrm{pOH}=2.30$
$\therefore \mathrm{pH}=14-2.30$
$=11.70$
Hence, the $\mathrm{pH}$ of the solution is $11.70 .$
(iii) $0.002 \mathrm{HBr}$ :
$\mathrm{HBr}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{Br}^{-}$
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{HBr}]$
$\Rightarrow\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=.002$
$\therefore \mathrm{pH}=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]$
$=-\log (0.002)$
$=2.69$
Hence, the $\mathrm{pH}$ of the solution is $2.69$.
(iv) $0.002 \mathrm{M} \mathrm{KOH}$ :
$\mathrm{KOH}_{(a q)} \longleftrightarrow \mathrm{K}_{(a q)}^{+}+\mathrm{OH}_{(a q)}^{-}$
$\left[\mathrm{OH}^{-}\right]=[\mathrm{KOH}]$
$\Rightarrow\left[\mathrm{OH}^{-}\right]=.002$
Now, $\mathrm{pOH}=-\log \left[\mathrm{OH}^{-}\right]$
$=2.69$
$\therefore \mathrm{pH}=14-2.69$
$=11.31$
Hence, the $\mathrm{pH}$ of the solution is $11.31$.
Question $49$ : Calculate the $\mathrm{pH}$ of the following solutions:
a) $2 \mathrm{~g}$ of TIOH dissolved in water to give 2 litre of solution.
b) $0.3 \mathrm{~g}$ of $\mathrm{Ca}(\mathrm{OH})_{2}$ dissolved in water to give $500 \mathrm{~mL}$ of solution.
c) $0.3 \mathrm{~g}$ of $\mathrm{NaOH}$ dissolved in water to give $200 \mathrm{~mL}$ of solution.
d) $1 \mathrm{~mL}$ of $13.6 \mathrm{M} \mathrm{HCl}$ is diluted with water to give 1 litre of solution.
Solution. (a) For $2 \mathrm{~g}$ of TIOH dissolved in water to give $2 \mathrm{~L}$ of solution:
$\left[\mathrm{TlOH}_{(a q)}\right]=\frac{2}{2} \mathrm{~g} / \mathrm{L}$
$=\frac{2}{2} \times \frac{1}{221} \mathrm{M}$
$=\frac{1}{221} \mathrm{M}$
$\mathrm{TlOH}_{(a q)} \longrightarrow \mathrm{Tl}_{(a q)}^{+}+\mathrm{OH}_{(a q)}^{-}$
$\left[\mathrm{OH}_{\left(\alpha_{4}\right)}^{-}\right]=\left[\mathrm{TlOH}_{(\alpha q)}\right]=\frac{1}{221} \mathrm{M}$
$K_{w}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]$
$10^{-14}=\left[\mathrm{H}^{+}\right]\left(\frac{1}{221}\right)$
$221 \times 10^{-14}=\left[\mathrm{H}^{+}\right]$
$\Rightarrow \mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]=-\log \left(221 \times 10^{-14}\right)$
$=-\log \left(2.21 \times 10^{-12}\right)$
$=11.65$
(b) For $0.3 \mathrm{~g}$ of $\mathrm{Ca}(\mathrm{OH})_{2}$ dissolved in water to give $500 \mathrm{~mL}$ of solution:
$\mathrm{Ca}(\mathrm{OH})_{2} \longrightarrow \mathrm{Ca}^{2+}+2 \mathrm{OH}^{-}$
$\left[\mathrm{Ca}(\mathrm{OH})_{2}\right]=0.3 \times \frac{1000}{500}=0.6 \mathrm{M}$
$\left[\mathrm{OH}^{-}_{a q}\right]=2 \times\left[\mathrm{Ca}(\mathrm{OH})_{2 \omega q}\right]=2 \times 0.6$
$=1.2 \mathrm{M}$
$\left[\mathrm{H}^{+}\right]=\frac{K_{w}}{\left[\mathrm{OH}^{-}{ }_{a q}\right]}$
$=\frac{10-14}{1.2} \mathrm{M}$
$=0.833 \times 10^{-14}$
$\mathrm{pH}=-\log \left(0.833 \times 10^{-14}\right)$
$=-\log \left(8.33 \times 10^{-13}\right)$
$=(-0.902+13)$
$=12.098$
(c) For $0.3 \mathrm{~g}$ of $\mathrm{NaOH}$ dissolved in water to give $200 \mathrm{~mL}$ of solution:
$\mathrm{NaOH} \longrightarrow \mathrm{Na}_{\left(a_{q)}\right.}^{+}+\mathrm{OH}_{(a q)}^{-}$
$[\mathrm{NaOH}]=0.3 \times \frac{1000}{200}=1.5 \mathrm{M}$
$\left[\mathrm{OH}^{-}{ }_{\omega q}\right]=1.5 \mathrm{M}$
$\left[\mathrm{OH}^{-}{ }_{\omega q}\right]=1.5 \mathrm{M}$
$=6.66 \times 10^{-13}$
$\mathrm{pH}=-\log \left(6.66 \times 10^{-13}\right)$
$=12.18$
(d) For $1 \mathrm{~mL}$ of $13.6 \mathrm{M} \mathrm{HCl}$ diluted with water to give $1 \mathrm{~L}$ of solution:
$13.6 \times 1 \mathrm{~mL}=\mathrm{M}_{2} \times 1000 \mathrm{~mL}$
(Before dilution) (After dilution)
$13.6 \times 10^{-3}=\mathrm{M}_{2} \times 1 \mathrm{~L}$
$\mathrm{M}_{2}=1.36 \times 10^{-2}$
$\left[\mathrm{H}^{+}\right]=1.36 \times 10^{-2}$
$\mathrm{pH}=-\log \left(1.36 \times 10^{-2}\right)$
$=(-0.1335+2)$
$=1.866 \sim 1.87$
Question $50$ The degree of ionization of a $0.1 \mathrm{M}$ bromoacetic acid solution is $0.132 .$ Calculate the $\mathrm{pH}$ of the solution and the $p K_{\mathrm{a}}$ of bromoacetic acid.
Solution. Degree of ionization, $\alpha=0.132$
Concentration, $c=0.1 \mathrm{M}$
Thus, the concentration of $\mathrm{H}_{3} \mathrm{O}^{+}=\mathrm{c.} \alpha$
$=0.1 \times 0.132$
$=0.0132$
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$=-\log (0.0132)$
$=1.879: 1.88$
Now,
$K_{o}=C \alpha^{2}$
$=0.1 \times(0.132)^{2}$
$K_{a}=.0017$
$p K_{a}=2.75$
Question 51: The $\mathrm{pH}$ of $0.005 \mathrm{M}$ codeine $\left(\mathrm{C}_{18} \mathrm{H}_{21} \mathrm{NO}_{3}\right)$ solution is $9.95 .$ Calculate its ionization constant and $\mathrm{pK}_{\mathrm{b}}$.
Solution. $c=0.005$
$\mathrm{pH}=9.95$
$\mathrm{pOH}=4.05$
$\mathrm{pH}=-\log (4.105)$
$4.05=-\log \left[\mathrm{OH}^{-}\right]$
$\left[\mathrm{OH}^{-}\right]=8.91 \times 10^{-5}$
$c \alpha=8.91 \times 10^{-5}$
$\alpha=\frac{8.91 \times 10^{-5}}{5 \times 10^{-3}}=1.782 \times 10^{-2}$
Thus, $K_{h}=c \alpha^{2}$
$=0.005 \times(1.782)^{2} \times 10^{-4}$
$=0.005 \times 3.1755 \times 10^{-4}$
$=0.0158 \times 10^{-4}$
$K_{b}=1.58 \times 10^{-6}$
$P k_{b}=-\log K_{b}$
$=-\log \left(1.58 \times 10^{-6}\right)$
$=5.80$
Question 52: What is the $\mathrm{pH}$ of $0.001 \mathrm{M}$ aniline solution? The ionization constant of aniline can be taken from Table 7.7. Calculate the degree of ionization of aniline in the solution. Also calculate the ionization constant of the conjugate acid of aniline.
Solution. $K_{b}=4.27 \times 10^{-10}$
$c=0.001 \mathrm{M}$
$\mathrm{pH}=?$
$\alpha=?$
$k_{b}=c \alpha^{2}$
$4.27 \times 10^{-10}=0.001 \times \alpha^{2}$
$4270 \times 10^{-10}=\alpha^{2}$
$65.34 \times 10^{-5}=\alpha=6.53 \times 10^{-4}$
Then, $[$ anion $]=c \alpha=.001 \times 65.34 \times 10^{-5}$
$=.065 \times 10^{-5}$
$\mathrm{pOH}=-\log \left(.065 \times 10^{-5}\right)$
$=6.187$
$\mathrm{pH}=7.813$
Now,
$K_{a} \times K_{b}=K_{w}$
$\therefore 4.27 \times 10^{-10} \times K_{a}=K_{w}$
$K_{a}=\frac{10^{-14}}{4.27 \times 10^{-10}}$
$=2.34 \times 10^{-5}$
Thus, the ionization constant of the conjugate acid of aniline is $2.34 \times 10^{-5}$.
Question 53: Calculate the degree of ionization of $0.05 \mathrm{M}$ acetic acid if its $\mathrm{pK}_{\mathrm{a}}$ value is $4.74 .$
Solution. $c=0.05 \mathrm{M}$
$p K_{a}=4.74$
$p K_{a}=-\log \left(K_{o}\right)$
$K_{a}=1.82 \times 10^{-5}$
$K_{a}=c \alpha^{2} \quad \alpha=\sqrt{\frac{K_{a}}{c}}$
$\alpha=\sqrt{\frac{1.82 \times 10^{-5}}{5 \times 10^{-2}}}=1.908 \times 10^{-2}$
When HCl is added to the solution, the concentration of $\mathrm{H}^{+}$ ions will increase. Therefore, the equilibrium will shift in the backward direction i.e., dissociation of acetic acid will decrease.
Case I: When $0.01 \mathrm{M} \mathrm{HCl}$ is taken.
Let $x$ be the amount of acetic acid dissociated after the addition of $\mathrm{HCl}$.
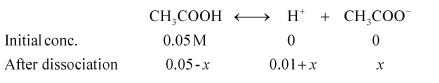
As the dissociation of a very small amount of acetic acid will take place, the values i.e., $0.05-x$ and $0.01+x$ can be taken as $0.05$ and $0.01$ respectively.
$K_{a}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}$
$\therefore K_{a}=\frac{(0.01) x}{0.05}$
$x=\frac{1.82 \times 10^{-5} \times 0.05}{0.01}$
$x=1.82 \times 10^{-3} \times 0.05 \mathrm{M}$
Now,
$\alpha=\frac{\text { Amount of acid dissociated }}{\text { Amount of acid taken }}$
$=\frac{1.82 \times 10^{-3} \times 0.05}{0.05}$
$=1.82 \times 10^{-3}$
Case II: When $0.1 \mathrm{M} \mathrm{HCl}$ is taken.
Let the amount of acetic acid dissociated in this case be $X$. As we have done in the first case, the concentrations of various species involved in the reaction are:
$\left[\mathrm{CH}_{3} \mathrm{COOH}\right]=0.05-X ; 0.05 \mathrm{M}$
$\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]=X$
$\left[\mathrm{H}^{+}\right]=0.1+X ; 0.1 \mathrm{M}$
$K_{a}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}$
$\therefore K_{o}=\frac{(0.1) X}{0.05}$
$x=\frac{1.82 \times 10^{-5} \times 0.05}{0.1}$
$x=1.82 \times 10^{-4} \times 0.05 \mathrm{M}$
Now,
$\alpha=\frac{\text { Amount of acid dissociated }}{\text { Amount of acid taken }}$
$=\frac{1.82 \times 10^{-4} \times 0.05}{0.05}$
$=1.82 \times 10^{-4}$
Question 54: The ionization constant of dimethylamine is $5.4 \times 10^{-4} .$ Calculate its degree of ionization in its $0.02 \mathrm{M}$ solution. What percentage of dimethylamine is ionized if the solution is also $0.1 \mathrm{M}$ in $\mathrm{NaOH} ?$
Solution. $K_{b}=5.4 \times 10^{-4}$
$c=0.02 \mathrm{M}$
Then, $\alpha=\sqrt{\frac{K_{b}}{c}}$
$=\sqrt{\frac{5.4 \times 10^{-4}}{0.02}}$
$=0.1643$
Now, if $0.1 \mathrm{M}$ of $\mathrm{NaOH}$ is added to the solution, then $\mathrm{NaOH}$ (being a strong base) undergoes complete ionization.
$\mathrm{NaOH}_{(a q)} \longleftrightarrow \mathrm{Na}_{(\text {ag) }}^{+}+\mathrm{OH}^{-}_{(a q)}$
$0.1 \mathrm{M} \quad 0.1 \mathrm{M}$
And,
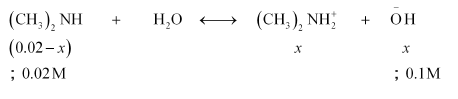
Then, $\left[\left(\mathrm{CH}_{3}\right)_{2} \mathrm{NH}_{2}^{+}\right]=x$
$\left[\mathrm{OH}^{-}\right]=x+0.1 ; 0.1$
$\Rightarrow K_{b}=\frac{\left[\left(\mathrm{CH}_{3}\right)_{2} \mathrm{NH}_{2}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\left(\mathrm{CH}_{3}\right)_{2} \mathrm{NH}\right]}$
$5.4 \times 10^{-4}=\frac{x \times 0.1}{0.02}$
$x=0.0054$
It means that in the presence of $0.1 \mathrm{M} \mathrm{NaOH}, 0.54 \%$ of dimethylamine will get dissociated.
Question $55$ : Calculate the hydrogen ion concentration in the following biological fluids whose $\mathrm{pH}$ are given below:
(a) Human muscle-fluid, $6.83$
(b) Human stomach fluid, $1.2$
(c) Human blood, $7.38$
(d) Human saliva, $6.4$.
Solution. (a) Human muscle fluid 6.83:
$\mathrm{pH}=6.83$
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$\therefore 6.83=-\log \left[\mathrm{H}^{+}\right]$
$\left[\mathrm{H}^{+}\right]=1.48 \times 10^{-7} \mathrm{M}$
(b) Human stomach fluid, 1.2:
$\mathrm{pH}=1.2$
$1.2=-\log \left[\mathrm{H}^{+}\right]$
$\therefore\left[\mathrm{H}^{+}\right]=0.063$
(c) Human blood, $7.38$ :
$\mathrm{pH}=7.38=-\log \left[\mathrm{H}^{+}\right]$
$\therefore\left[\mathrm{H}^{+}\right]=4.17 \times 10^{-8} \mathrm{M}$
(d) Human saliva, $6.4$ :
$\mathrm{pH}=6.4$
$6.4=-\log \left[\mathrm{H}^{+}\right]$
$\left[\mathrm{H}^{+}\right]=3.98 \times 10^{-7}$
Question $56$ : The $\mathrm{pH}$ of milk, black coffee, tomato juice, lemon juice and egg white are $6.8,5.0,4.2,2.2$ and $7.8$ respectively. Calculate corresponding hydrogen ion concentration in each.
Solution. The hydrogen ion concentration in the given substances can be calculated by using the given relation:
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
(i) $\mathrm{pH}$ of milk $=6.8$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$6.8=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-6.8$
$\left[\mathrm{H}^{+}\right]=\operatorname{anitlog}(-6.8)$
$=1.5 \times 10^{-7} \mathrm{M}$
(ii) $\mathrm{pH}$ of black coffee $=5.0$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$5.0=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-5.0$
$\left[\mathrm{H}^{+}\right]=$ anitlog $(-5.0)$
$=10^{-5} \mathrm{M}$
(iii) $\mathrm{pH}$ of tomato juice $=4.2$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$4.2=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-4.2$
$\left[\mathrm{H}^{+}\right]=\operatorname{anitlog}(-4.2)$
$=6.31 \times 10^{-5} \mathrm{M}$
(iv) $\mathrm{pH}$ of lemon juice $=2.2$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$2.2=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-2.2$
$\left[\mathrm{H}^{+}\right]=\operatorname{anitlog}(-2.2)$
$=6.31 \times 10^{-3} \mathrm{M}$
(v) $\mathrm{pH}$ of egg white $=7.8$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$7.8=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-7.8$
$\left[\mathrm{H}^{+}\right]=\operatorname{anitlog}(-7.8)$
$=1.58 \times 10^{-8} \mathrm{M}$
Question $57:$ If $0.561 \mathrm{~g}$ of $\mathrm{KOH}$ is dissolved in water to give $200 \mathrm{~mL}$ of solution at $298 \mathrm{~K}$. Calculate the concentrations of potassium, hydrogen and hydroxyl ions. What is its $\mathrm{pH}$ ?
Solution. $\left[\mathrm{KOH}_{a q}\right]=\frac{0.561}{\frac{1}{5}} \mathrm{~g} / L$
$=2.805 \mathrm{~g} / L$
$=2.805 \times \frac{1}{56.11} \mathrm{M}$
$=.05 \mathrm{M}$
$\mathrm{KOH}_{(a q)} \rightarrow \mathrm{K}_{(a q)}^{+}+\mathrm{OH}_{(a q)}^{-}$
$\left[\mathrm{OH}^{-}\right]=.05 \mathrm{M}=\left[\mathrm{K}^{+}\right]$
$\left[\mathrm{H}^{+}\right]\left[\mathrm{H}^{-}\right]=K_{\mathrm{w}}$
$\left[\mathrm{H}^{+}\right] \frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}$
$=\frac{10^{-14}}{0.05}=2 \times 10^{-13} \mathrm{M}$
$=\frac{10^{-14}}{0.05}=2 \times 10^{-13} \mathrm{M}$
$\therefore \mathrm{pH}=12.70$
Question $58:$ The solubility of $\mathrm{Sr}(\mathrm{OH})_{2}$ at $298 \mathrm{~K}$ is $19.23 \mathrm{~g} / \mathrm{L}$ of solution. Calculate the concentrations of strontium and hydroxyl ions and the $\mathrm{pH}$ of the solution.
Solution. Solubility of $\mathrm{Sr}(\mathrm{OH})_{2}=19.23 \mathrm{~g} / \mathrm{L}$
Then, concentration of $\mathrm{Sr}(\mathrm{OH})_{2}$
$=\frac{19.23}{121.63} \mathrm{M}$
$=0.1581 \mathrm{M}$
$\mathrm{Sr}(\mathrm{OH})_{2(a q)} \longrightarrow \mathrm{Sr}^{2+}{ }_{(\mathrm{aq})}+2\left(\mathrm{OH}^{-}\right)_{(a q)}$
$\therefore\left[\mathrm{Sr}^{2+}\right]=0.1581 \mathrm{M}$
$\left[\mathrm{OH}^{-}\right]=2 \times 0.1581 \mathrm{M}=0.3126 \mathrm{M}$
Now,
$K_{w}=\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}^{+}\right]$
$\frac{10^{-14}}{0.3126}=\left[\mathrm{H}^{+}\right]$
$\Rightarrow\left[\mathrm{H}^{+}\right]=3.2 \times 10^{-14}$
$\therefore \mathrm{pH}=13.495 ; 13.50$
Question 59: The ionization constant of propanoic acid is $1.32 \times 10^{-5} .$ Calculate the degree of ionization of the acid in its $0.05 \mathrm{M}$ solution and also its $\mathrm{pH}$. What will be its degree of ionization if the solution is $0.01 \mathrm{M}$ in $\mathrm{HCl}$ also?
Solution. Let the degree of ionization of propanoic acid be $\alpha$.
Then, representing propionic acid as HA, we have:
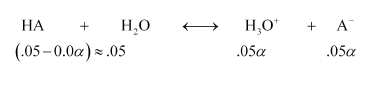
$K_{a}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}$
$=\frac{(.05 \alpha)(.05 \alpha)}{0.05}=.05 \alpha^{2}$
$\alpha=\sqrt{\frac{K_{a}}{.05}}=1.63 \times 10^{-2}$
Then, $\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=.05 \alpha=.05 \times 1.63 \times 10^{-2}=K_{b} .15 \times 10^{-4} \mathrm{M}$
$\therefore \mathrm{pH}=3.09$
In the presence of $0.1 \mathrm{M}$ of $\mathrm{HCl}$, let $\alpha$ ' be the degree of ionization.
Then, $\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=0.01$
$\left[\mathrm{A}^{-}\right]=005 \alpha^{\prime}$
$[\mathrm{HA}]=.05$
$K_{a}=\frac{0.01 \times .05 \alpha^{\prime}}{.05}$
$1.32 \times 10^{-5}=.01 \times \alpha^{\prime}$
$\alpha^{\prime}=1.32 \times 10^{-3}$
Question $60:$ The $\mathrm{pH}$ of $0.1 \mathrm{M}$ solution of cyanic acid (HCNO) is 2.34. Calculate the ionization constant of the acid and its degree of ionization in the solution.
Solution. $c=0.1 \mathrm{M}$
$\mathrm{pH}=2.34$
$-\log \left[\mathrm{H}^{+}\right]=\mathrm{pH}$
$-\log \left[\mathrm{H}^{+}\right]=2.34$
$\left[\mathrm{H}^{+}\right]=4.5 \times 10^{-3}$
Also,
$\left[\mathrm{H}^{+}\right]=c \alpha$
$4.5 \times 10^{-3}=0.1 \times \alpha$
$\frac{4.5 \times 10^{-3}}{0.1}=\alpha$
$\alpha=45 \times 10^{-3}=.045$
Then,
$K_{a}=c \alpha^{2}$
$=0.1 \times\left(45 \times 10^{-3}\right)^{2}$
$=202.5 \times 10^{-6}$
$=2.02 \times 10^{-4}$
Question 61: The ionization constant of nitrous acid is $4.5 \times 10^{-4} .$ Calculate the pH of $0.04 \mathrm{M}$ sodium nitrite solution and also its degree of hydrolysis.
Solution. $\mathrm{NaNO}_{2}$ is the salt of a strong base ( $\mathrm{NaOH}$ ) and a weak acid $\left(\mathrm{HNO}_{2}\right) .$
$\mathrm{NO}_{2}^{-}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{HNO}_{2}+\mathrm{OH}^{-}$
$K_{h}=\frac{\left[\mathrm{HNO}_{2}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NO}_{2}^{-}\right]}$
$\Rightarrow \frac{K_{w}}{K_{a}}=\frac{10^{-14}}{4.5 \times 10^{-4}}=.22 \times 10^{-10}$
Now, If $x$ moles of the salt undergo hydrolysis, then the concentration of various species present in the solution will be
$\left[\mathrm{NO}_{2}^{-}\right]=.04-x ; 0.04$
$\left[\mathrm{HNO}_{2}\right]=x$
$\left[\mathrm{OH}^{-}\right]=x$
$K_{h}=\frac{x^{2}}{0.04}=0.22 \times 10^{-10}$
$x^{2}=.0088 \times 10^{-10}$
$x=.093 \times 10^{-5}$
$\therefore\left[\mathrm{OH}^{-}\right]=0.093 \times 10^{-5} \mathrm{M}$
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{10^{-14}}{.093 \times 10^{-5}}=10.75 \times 10^{-9} \mathrm{M}$
$\Rightarrow \mathrm{pH}=-\log \left(10.75 \times 10^{-9}\right)$
$=7.96$
Therefore, degree of hydrolysis
$=\frac{x}{0.04}=\frac{.093 \times 10^{-5}}{.04}=2.325 \times 10^{-5}$
Question $62$ : A $0.02 \mathrm{M}$ solution of pyridinium hydrochloride has $\mathrm{pH}=3.44$. Calculate the ionization constant of pyridine
Solution. $\mathrm{pH}=3.44$
We know that,
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$\therefore\left[\mathrm{H}^{+}\right]=3.63 \times 10^{-4}$
Then, $K_{h}=\frac{\left(3.63 \times 10^{-4}\right)^{2}}{0.02}$
$(\because$ concentration $=0.02 \mathrm{M})$
$\Rightarrow K_{h}=6.6 \times 10^{-6}$
$\mathrm{Now}, K_{h}=\frac{K_{w}}{K_{a}}$
$\Rightarrow K_{a}=\frac{K_{w}}{K_{h}}=\frac{10^{-14}}{6.6 \times 10^{-6}}$
$=1.51 \times 10^{-9}$
Question 63: Predict if the solutions of the following salts are neutral, acidic or basic:
$\mathrm{NaCl}, \mathrm{KBr}, \mathrm{NaCN}, \mathrm{NH}_{4} \mathrm{NO}_{3}, \mathrm{NaNO}_{2}$ and $\mathrm{KF}$
Solution. (i) $\mathrm{NaCl}$ :
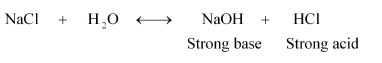
Therefore, it is a neutral solution.
(ii) KBr:

Therefore, it is a neutral solution.
(iii) NaCN:

Therefore, it is a basic solution.
(iv) $\mathrm{NH}_{4} \mathrm{NO}_{3}$

Therefore, it is an acidic solution.
(v) $\mathrm{NaNO}_{2}$
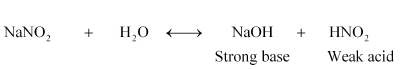
Therefore, it is a basic solution.
(vi) $\mathrm{KF}$
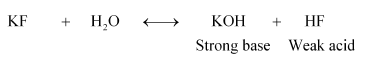
Therefore, it is a basic solution.
Question 64: The ionization constant of chloroacetic acid is $1.35 \times 10^{-3}$. What will be the $\mathrm{pH}$ of $0.1 \mathrm{M}$ acid and its $0.1 \mathrm{M}$ sodium salt solution?
Solution. It is given that $K_{a}$ for $\mathrm{ClCH}_{2} \mathrm{COOH}$ is $1.35 \times 10^{-3}$.
$\Rightarrow K_{a}=c \alpha^{2}$
$\therefore \alpha=\sqrt{\frac{K_{a}}{c}}$
$=\sqrt{\frac{1.35 \times 10^{-3}}{0.1}}$
$(\therefore$ concentration of acid $=0.1 \mathrm{~m})$
$\alpha=\sqrt{1.35 \times 10^{-2}}$
$=0.116$
$\therefore\left[\mathrm{H}^{+}\right]=c \alpha=0.1 \times 0.116$
$=.0116$
$\Rightarrow \mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]=1.94$
$\mathrm{CICH}_{2} \mathrm{COONa}$ is the salt of a weak acid i.e., $\mathrm{ClCH}_{2} \mathrm{COOH}$ and a strong base i.e., $\mathrm{NaOH}$.
$\mathrm{ClCH}_{2} \mathrm{COO}^{-}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{ClCH}_{2} \mathrm{COOH}+\mathrm{OH}^{-}$
$K_{h}=\frac{\left[\mathrm{ClCH}_{2} \mathrm{COOH}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{ClCH}_{2} \mathrm{COO}^{-}\right]}$
$K_{h}=\frac{K_{w}}{K_{a}}$
$K_{h}=\frac{10^{-14}}{1.35 \times 10^{-3}}$
$=0.740 \times 10^{-11}$
Also, $K_{h}=\frac{x^{2}}{0.1}$
(where $x$ is the concentration of $\mathrm{OH}^{-}$ and $\left.\mathrm{ClCH}_{2} \mathrm{COOH}\right)$
$0.740 \times 10^{-11}=\frac{x^{2}}{0.1}$
$0.074 \times 10^{-11}=x^{2}$
$\Rightarrow x^{2}=0.74 \times 10^{-12}$
$x=0.86 \times 10^{-6}$
$\left[\mathrm{OH}^{-}\right]=0.86 \times 10^{-6}$
$\therefore\left[\mathrm{H}^{+}\right]=\frac{K_{w}}{0.86 \times 10^{-6}}$
$=\frac{10^{-14}}{0.86 \times 10^{-6}}$
$\left[\mathrm{H}^{+}\right]=1.162 \times 10^{-8}$
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$=7.94$
Question $65$ :lonic product of water at $310 \mathrm{~K}$ is $2.7 \times 10^{-14}$. What is the pH of neutral water at this temperature?
Solution. lonic product,
$K_{w}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]$
$\operatorname{Let}\left[\mathrm{H}^{+}\right]=x$
Since $\left[\mathrm{H}^{+}\right]=\left[\mathrm{OH}^{-}\right], K_{\mathrm{w}}=x^{2}$
$\Rightarrow K_{\mathrm{w}}$ at $310 \mathrm{~K}$ is $2.7 \times 10^{-14}$
$\therefore 2.7 \times 10^{-14}=x^{2}$
$\Rightarrow x=1.64 \times 10^{-7}$
$\Rightarrow\left[\mathrm{H}^{+}\right]=1.64 \times 10^{-7}$
$\Rightarrow \mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$=-\log \left[1.64 \times 10^{-7}\right]$
$=6.78$
Question 66: Calculate the $\mathrm{pH}$ of the resultant mixtures:
a) $10 \mathrm{~mL}$ of $0.2 \mathrm{M} \mathrm{Ca}(\mathrm{OH})_{2}+25 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{HCl}$
b) $10 \mathrm{~mL}$ of $0.01 \mathrm{M} \mathrm{H}_{2} \mathrm{SO}_{4}+10 \mathrm{~mL}$ of $0.01 \mathrm{M} \mathrm{Ca}(\mathrm{OH})_{2}$
c) $10 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{H}_{2} \mathrm{SO}_{4}+10 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{KOH}$
Solution. (a) Moles of $\mathrm{H}_{3} \mathrm{O}^{+}=\frac{25 \times 0.1}{1000}=.0025 \mathrm{~mol}$
Moles of $\mathrm{OH}^{-}=\frac{10 \times 0.2 \times 2}{1000}=.0040 \mathrm{~mol}$
Thus, excess of $\mathrm{OH}^{-}=.0015 \mathrm{~mol}$
$\left[\mathrm{OH}^{-}\right]=\frac{.0015}{35 \times 10^{-3}} \mathrm{~mol} / \mathrm{L}=.0428$
$\mathrm{pOH}=-\log [\mathrm{OH}]$
$=1.36$
$\mathrm{pH}=14-1.36$
$=12.63 \quad$ (not matched)
(b) Moles of $\mathrm{H}_{3} \mathrm{O}^{+}=\frac{2 \times 10 \times 0.01}{1000}=.0002
\mathrm{~mol}$
Moles of $\mathrm{OH}^{-}=\frac{2 \times 10 \times .01}{1000}=.0002 \mathrm{~mol}$
Since there is neither an excess of $\mathrm{H}_{3} \mathrm{O}^{+}$ or $\mathrm{OH}^{-}$, the solution is neutral. Hence, $\mathrm{pH}=7$.
(c) Moles of $\mathrm{H}_{3} \mathrm{O}^{+}=\frac{2 \times 10 \times 0.1}{1000}=.002 \mathrm{~mol}$
Moles of $\mathrm{OH}^{-}=\frac{10 \times 0.1}{1000}=0.001 \mathrm{~mol}$
Excess of $\mathrm{H}_{3} \mathrm{O}^{+}=.001 \mathrm{~mol}$
Thus, $\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{.001}{20 \times 10^{-3}}$
$=\frac{10^{-3}}{20 \times 10^{-3}}=.05$
$\therefore \mathrm{pH}=-\log (0.05)$
$=1.30$
Question 67: Determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at $298 \mathrm{~K}$ from their solubility product constants given in Table $7.9$ (page 221). Determine also the molarities of individual ions.
Solution. (1) Silver chromate:
$\mathrm{Ag}_{2} \mathrm{CrO}_{4} \longrightarrow 2 \mathrm{Ag}^{+}+\mathrm{CrO}_{4}^{2-}$
Then,
$K_{s p}=\left[\mathrm{Ag}^{+}\right]^{2}\left[\mathrm{CrO}_{4}{ }^{2-}\right]$
$\Rightarrow 1.1 \times 10^{-12}=4 s^{3}$
$.275 \times 10^{-12}=s^{3}$
$s=0.65 \times 10^{-4} \mathrm{M}$
Molarity of $\mathrm{Ag}^{+}=2 \mathrm{~s}=2 \times 0.65 \times 10^{-4}$
$=1.30 \times 10^{-4} \mathrm{M}$
Molarity of $\mathrm{CrO}_{4}{ }^{2-}=s=0.65 \times 10^{-4} \mathrm{M}$
(2) Barium chromate:
$\mathrm{BaCrO}_{4} \longrightarrow \mathrm{Ba}^{2+}+\mathrm{CrO}_{4}^{2-}$
Then, $K_{s p}=\left[\mathrm{Ba}^{2+}\right]\left[\mathrm{CrO}_{4}^{2-}\right]$
Let $s$ be the solubility of $\mathrm{BaCrO}_{4}$.
Thus, $\left[\mathrm{Ba}^{2+}\right]=\mathrm{s}$ and $\left[\mathrm{CrO}_{4}{ }^{2-}\right]=\mathrm{s}$
$\Rightarrow K_{S P}=s^{2}$
$\Rightarrow 1.2 \times 10^{-10}=s^{2}$
$\Rightarrow s=1.09 \times 10^{-5} \mathrm{M}$
Molarity of $\mathrm{Ba}^{2+}=$ Molarity of $\mathrm{CrO}_{4}{ }^{2-}=s=1.09 \times 10^{-5} \mathrm{M}$
(3) Ferric hydroxide:
$\mathrm{Fe}(\mathrm{OH})_{3} \longrightarrow \mathrm{Fe}^{2+}+3 \mathrm{OH}^{-}$
$K_{s p}=\left[\mathrm{Fe}^{2+}\right]\left[\mathrm{OH}^{-}\right]^{3}$
Let $s$ be the solubility of $\mathrm{Fe}(\mathrm{OH})_{3}$.
Thus, $\left[\mathrm{Fe}^{3+}\right]=s$ and $\left[\mathrm{OH}^{-}\right]=3 s$
$\Rightarrow K_{s p}=s .(3 s)^{3}$
$=s .27 s^{3}$
$K_{s p}=27 s^{4}$
$1.0 \times 10^{-38}=27 s^{4}$
$.037 \times 10^{-38}=s^{4}$
$.00037 \times 10^{-36}=s^{4} \quad \Rightarrow 1.39 \times 10^{-10} \mathrm{M}=\mathrm{S}$
Molarity of $\mathrm{Fe}^{3+}=s=1.39 \times 10^{-10} \mathrm{M}$
Molarity of $\mathrm{OH}^{-}=3 s=4.17 \times 10^{-10} \mathrm{M}$
(4) Lead chloride:
$\mathrm{PbCl}_{2} \longrightarrow \mathrm{Pb}^{2+}+2 \mathrm{Cl}^{-}$
$K_{S P}=\left[\mathrm{Pb}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}$
Let $K_{S P}$ be the solubility of $\mathrm{PbCl}_{2}$.
$\left[\mathrm{PB}^{2+}\right]=s$ and $\left[\mathrm{Cl}^{-}\right]=2 s$
Thus, $K_{s p}=s .(2 s)^{2}$
$=4 s^{3}$
$\Rightarrow 1.6 \times 10^{-5}=4 s^{3}$
$\Rightarrow 0.4 \times 10^{-5}=s^{3}$
$4 \times 10^{-6}=s^{3} \Rightarrow 1.58 \times 10^{-2} \mathrm{M}=\mathrm{S} .1$
Molarity of $\mathrm{PB}^{2+}=s=1.58 \times 10^{-2} \mathrm{M}$
Molarity of chloride $=2 s=3.16 \times 10^{-2} \mathrm{M}$
(5) Mercurous iodide:
$\mathrm{Hg}_{2} \mathrm{I}_{2} \longrightarrow \mathrm{Hg}^{2+}+2 \mathrm{I}^{-}$
$K_{s p}=\left[\mathrm{Hg}_{2}^{2+}\right]^{2}\left[\mathrm{I}^{-}\right]^{2}$
Let $\mathrm{s}$ be the solubility of $\mathrm{Hg}_{2} \mathrm{I}_{2}$.
$\Rightarrow\left[\mathrm{Hg}_{2}^{2+}\right]=s$ and $\left[\mathrm{I}^{-}\right]=2 s$
Thus, $K_{x p}=s(2 s)^{2} \Rightarrow K_{s p}=4 s^{3}$
$4.5 \times 10^{-29}=4 s^{3}$
$1.125 \times 10^{-29}=s^{3}$
$\Rightarrow s=2.24 \times 10^{-10} \mathrm{M}$
Molarity of $\mathrm{Hg}_{2}^{2+}=s=2.24 \times 10^{-10} \mathrm{M}$
Molarity of $\mathrm{I}^{-}=2 s=4.48 \times 10^{-10} \mathrm{M}$
Question $68:$ The solubility product constant of $\mathrm{Ag}_{2} \mathrm{CrO}_{4}$ and $\mathrm{AgBr}$ are $1.1 \times 10^{-12}$ and $5.0 \times 10^{-13}$ respectively. Calculate the ratio of the molarities of their saturated solutions.
Solution. Let $s$ be the solubility of $\mathrm{Ag}_{2} \mathrm{CrO}_{4}$
Then, $\mathrm{Ag}_{2} \mathrm{CrO}_{4} \longleftrightarrow \mathrm{Ag}^{2+}+2 \mathrm{CrO}_{4}^{-}$
$K_{s p}=(2 s)^{2} . s=4 s^{3}$
$1.1 \times 10^{-12}=4 s^{3}$
$s=6.5 \times 10^{-5} \mathrm{M}$
Let $s^{\prime}$ be the solubility of $\mathrm{AgBr}$.
$\mathrm{AgBr}_{(s)} \longleftrightarrow \mathrm{Ag}^{+}+\mathrm{Br}^{-}$
$K_{s p}=s^{\prime 2}=5.0 \times 10^{-13}$
$\therefore s^{\prime}=7.07 \times 10^{-7} \mathrm{M}$
Therefore, the ratio of the molarities of their saturated solution is
$\frac{s}{s^{\prime}}=\frac{6.5 \times 10^{-5} \mathrm{M}}{7.07 \times 10^{-7} \mathrm{M}}=91.9$
Question $69:$ Equal volumes of $0.002 \mathrm{M}$ solutions of sodium iodate and cupric chlorate are mixed together. Will it lead to precipitation of copper iodate? (For cupric iodate $K_{\mathrm{sp}}=7.4 \times 10^{-8}$ ).
Solution. When equal volumes of sodium iodate and cupric chlorate solutions are mixed together, then the molar concentrations of both solutions are reduced to half i.e., $0.001 \mathrm{M}$.
Then,
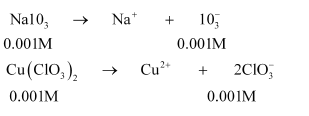
Now, the solubility equilibrium for copper iodate can be written as:
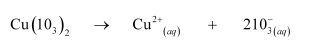
Ionic product of copper iodate:
$=\left[\mathrm{Cu}^{2+}\right]\left[10_{3}^{-}\right]^{2}$
$=(0.001)(0.001)^{2}$
$=1 \times 10^{-9}$
Since the ionic product $\left(1 \times 10^{-9}\right)$ is less than $K_{s p}\left(7.4 \times 10^{-8}\right)$, precipitation will not occur.
Question 70: The ionization constant of benzoic acid is $6.46 \times 10^{-5}$ and $K_{\mathrm{sp}}$ for silver benzoate is $2.5 \times 10^{-13}$. How many times is silver benzoate more soluble in a buffer of $\mathrm{pH} 3.19$ compared to its solubility in pure water?
Solution. Since $\mathrm{pH}=3.19$
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=6.46 \times 10^{-4} \mathrm{M}$
$\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}+\mathrm{H}_{3} \mathrm{O}$
$K_{a} \frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}\right]}$
$\frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{a}}=\frac{6.46 \times 10^{-4}}{6.46 \times 10^{-5}}=10$
Let the solubility of $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOAg}$ be $\times \mathrm{mol} / \mathrm{L}$.
Then,
$\left[\mathrm{Ag}^{+}\right]=x$
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}\right]+\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]=x$
$10\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]+\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]=x$
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]=\frac{x}{11}$
$K_{s p}\left[\mathrm{Ag}^{+}\right]\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]$
$2.5 \times 10^{-13}=x\left(\frac{x}{11}\right)$
$x=1.66 \times 10^{-6} \mathrm{~mol} / \mathrm{L}$
Thus, the solubility of silver benzoate in a $\mathrm{pH} 3.19$ solution is $1.66 \times 10^{-6} \mathrm{~mol} / \mathrm{L}$.
Now, let the solubility of $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOAg}$ be $\mathrm{x}^{\prime} \mathrm{mol} / \mathrm{L}$.
Then, $\left[\mathrm{Ag}^{+}\right]=x^{\prime} \mathrm{M}$ and $\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]=x^{\prime} \mathrm{M}$.
$K_{s p}=\left[\mathrm{Ag}^{+}\right]\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]$
$K_{s p}=\left(x^{\prime}\right)^{2}$
$x^{\prime}=\sqrt{K_{s p}}=\sqrt{2.5 \times 10^{-13}}=5 \times 10^{-7} \mathrm{~mol} / \mathrm{L}$
$\therefore \frac{x}{x^{\prime}}=\frac{1.66 \times 10^{-6}}{5 \times 10^{-7}}=3.32$
Hence, $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOAg}$ is approximately $3.317$ times more soluble in a low $\mathrm{pH}$ solution.
Question 71: What is the maximum concentration of equimolar solutions of ferrous sulphate and sodium sulphide so that when mixed in equal volumes, there is no precipitation of iron sulphide? (For iron sulphide, $K_{\text {sp }}=6.3 \times 10^{-18}$ )
Solution. Let the maximum concentration of each solution be $x \mathrm{~mol} / \mathrm{L} .$ After mixing, the volume of the concentrations of each solution will be reduced to half i.e., $\frac{x}{2}$
$\therefore\left[\mathrm{FeSO}_{4}\right]=\left[\mathrm{Na}_{2} \mathrm{~S}\right]=\frac{x}{2} \mathrm{M}$
Then, $\left[\mathrm{Fe}^{2+}\right]=\left[\mathrm{FeSO}_{4}\right]=\frac{x}{2} \mathrm{M}$
Also, $\left[\mathrm{S}^{2-}\right]=\left[\mathrm{Na}_{2} \mathrm{~S}\right]=\frac{x}{2} \mathrm{M}$
$\mathrm{FeS}_{(s)} \longleftrightarrow \mathrm{Fe}_{(a q)}^{2+}+\mathrm{S}_{(a q)}^{2-}$
$K_{s p}=\left[\mathrm{Fe}^{2+}\right]\left[\mathrm{S}^{2-}\right]$
$6.3 \times 10^{-18}=\left(\frac{x}{2}\right)\left(\frac{x}{2}\right)$
$\frac{x^{2}}{4}=6.3 \times 10^{-18}$
$\Rightarrow x=5.02 \times 10^{-9}$
If the concentrations of both solutions are equal to or less than $5.02 \times 10^{-9} \mathrm{M}$, then there will be no precipitation of iron sulphide.
Question $72$ : What is the minimum volume of water required to dissolve $1 \mathrm{~g}$ of calcium sulphate at $298 \mathrm{~K} ?$ (For calcium sulphate, $K_{\mathrm{sp}}$ is $\left.9.1 \times 10^{-6}\right)$
Solution. $\mathrm{CaSO}_{4(s)} \longleftrightarrow \mathrm{Ca}^{2+}{(a q)}+\mathrm{SO}_{4}^{2-}(a q)$
$K_{s p}=\left[\mathrm{Ca}^{2+}\right]\left[\mathrm{SO}_{4}^{2-}\right]$
Let the solubility of $\mathrm{CaSO}_{4}$ be $s$.
Then, $K_{s p}=s^{2}$
$9.1 \times 10^{-6}=s^{2}$
$s=3.02 \times 10^{-3} \mathrm{~mol} / \mathrm{L}$
Molecular mass of $\mathrm{CaSO}_{4}=136 \mathrm{~g} / \mathrm{mol}$
Solubility of $\mathrm{CaSO}_{4}$ in gram $/ \mathrm{L}=3.02 \times 10^{-3} \times 136$
$=0.41 \mathrm{~g} / \mathrm{L}$
This means that we need $1 \mathrm{~L}$ of water to dissolve $0.41 \mathrm{~g}$ of $\mathrm{CaSO}_{4}$
Therefore, to dissolve $1 \mathrm{~g}$ of $\mathrm{CaSO}_{4}$ we require $=\frac{1}{0.41} \mathrm{~L}=2.44 \mathrm{~L}$ of water.
Question 73: The concentration of sulphide ion in $0.1 \mathrm{M} \mathrm{HCl}$ solution saturated with hydrogen sulphide is $1.0 \times 10^{-19} \mathrm{M}$. If $10 \mathrm{~mL}$ of this is added to $5 \mathrm{~mL}$ of $0.04 \mathrm{M}$ solution of the following:
$\mathrm{FeSO}_{4}, \mathrm{MnCl}_{2}, \mathrm{ZnCl}_{2}$ and $\mathrm{CdCl}_{2}$. in which of these solutions precipitation will take place?
Given $K_{x p}$ for $\mathrm{FeS}=6.3 \times 10^{-18}, \mathrm{MnS}=2.5 \times 10^{-13}, \mathrm{ZnS}=1.6 \times 10^{-2+}$
$\mathrm{CdS}=8.0 \times 10^{-27}$
Solution. For precipitation to take place, it is required that the calculated ionic product exceeds the $K_{s p}$ value.
Before mixing:
$\left[\mathrm{S}^{2-}\right]=1.0 \times 10^{-19} \mathrm{M}\left[\mathrm{M}^{2+}\right]=0.04 \mathrm{M}$
volume $=10 \mathrm{~mL} \quad$ volume $=5 \mathrm{~mL}$
After mixing:
$\begin{array}{ll}{\left[\mathrm{S}^{2-}\right]=?} & {\left[\mathrm{M}^{2+}\right]=?} \\ \text { volume }=(10+5)=15 \mathrm{~mL} & \text { volume }=15 \mathrm{~mL}\end{array}$
volume $=(10+5)=15 \mathrm{~mL} \quad$ volume $=15 \mathrm{~mL}$
$\left[\mathrm{S}^{2-}\right]=\frac{1.0 \times 10^{-19} \times 10}{15}=6.67 \times 10^{-20} \mathrm{M}$
$\left[\mathrm{M}^{2+}\right]=\frac{0.04 \times 5}{15}=1.33 \times 10^{-2} \mathrm{M}$
Ionic product $=\left[\mathrm{M}^{2+}\right]\left[\mathrm{S}^{2-}\right]$
$=\left(1.33 \times 10^{-2}\right)\left(6.67 \times 10^{-20}\right)$
$=8.87 \times 10^{-22}$
This ionic product exceeds the $K_{s p}$ of Zns and CdS. Therefore, precipitation will occur in $\mathrm{CdCl}_{2}$ and $\mathrm{ZnCl}_{2}$ solutions.
So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.
Also Read,
Class 11 Chemistry Notes Download.
Class 11 Chemistry Book Chapterwise Download.
Class 11 Chemistry Exemplar Chapterwise Download.
If you have any Confusion related to NCERT Solutions for Class 11 Chemistry chapter 7 Equilibrium PDF then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 11 Chemistry by Kota’s top IITian’s Faculties Install the eSaral App
In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 7 Equilibrium in PDF that are prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to learn and understand class 11 Chemistry chapter 7 "Equilibrium" in an easy way then you can use these solutions PDF.
NCERT Solutions helps students to Practice important concepts of subjects easily. Class 11 Chemistry solutions provide detailed explanations of all the NCERT questions that students can use to clear their doubts instantly.
If you want to score high in your class 11 Chemistry Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.
In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 7 Equilibrium PDF that you can download to start your preparations anytime.
So, without wasting more time Let’s start.
Download NCERT Solutions for Class 11 Chemistry chapter 7 Equilibrium PDF"
Question $.1:$ A liquid is in equilibrium with its vapour in a sealed container at a fixed temperature. The volume of the container is suddenly increased.a) What is the initial effect of the change on vapour pressure?
b) How do rates of evaporation and condensation change initially?
c) What happens when equilibrium is restored finally and what will be the final vapour pressure?
Solution . (a) If the volume of the container is suddenly increased, then the vapour pressure would decrease initially. This is because the amount of vapour remains the same, but the volume increases suddenly. As a result, the same amount of vapour is distributed in a larger volume
(b) Since the temperature is constant, the rate of evaporation also remains constant. When the volume of the container is increased, the density of the vapour phase decreases. As a result, the rate of collisions of the vapour particles also decreases. Hence, the rate of condensation decreases initially.
(c) When equilibrium is restored finally, the rate of evaporation becomes equal to the rate of condensation. In this case, only the volume changes while the temperature remains constant. The
vapour pressure depends on temperature and not on volume. Hence, the final vapour pressure will be equal to the original vapour pressure of the system
Question 2: What is $K_{c}$ for the following equilibrium when the equilibrium concentration of each substance is: $\left[\mathrm{SO}_{2}\right]=0.60 \mathrm{M},\left[\mathrm{O}_{2}\right]=0.82 \mathrm{M}$ and $\left[\mathrm{SO}_{3}\right]=1.90 \mathrm{M} ?$
Solution. The equilibrium constant $\left(\mathrm{K}_{c}\right)$ for the give reaction is:
$\mathrm{K}_{c}=\frac{\left[\mathrm{SO}_{3}\right]^{2}}{\left[\mathrm{SO}_{2}\right]^{2}\left[\mathrm{O}_{2}\right]}$
$=\frac{(1.90)^{2} \mathrm{M}^{2}}{(0.60)^{2}(0.821) \mathrm{M}^{3}}$
$=12.239 \mathrm{M}^{-1}$ (approximately)
Hence, $K_{c}$ for the equilibrium is $12.239 \mathrm{M}^{-1}$.
Question 3: At a certain temperature and total pressure of $10^{5} \mathrm{~Pa}$, iodine vapour contains $40 \%$ by volume of $\mathrm{I}$ atoms
$\mathrm{I}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{I}(\mathrm{g})$
Calculate $K_{p}$ for the equilibrium.
Solution. Partial pressure of I atoms,
$p_{1}=\frac{40}{100} \times p_{\text {total }}$
$=\frac{40}{100} \times 10^{5}$
$=4 \times 10^{4} \mathrm{~Pa}$
Partial pressure of $\mathrm{I}_{2}$ molecules,
$p_{\mathrm{I}_{2}}=\frac{60}{100} \times p_{\text {total }}$
$=\frac{60}{100} \times 10^{5}$
$=6 \times 10^{4} \mathrm{~Pa}$
Now, for the given reaction,
$K_{p}=\frac{(p \mathrm{I})^{2}}{p_{1_{2}}}$
$=\frac{\left(4 \times 10^{4}\right)^{2} \mathrm{~Pa}^{2}}{6 \times 10^{4} \mathrm{~Pa}}$
$=2.67 \times 10^{4} \mathrm{~Pa}$
Question 4: Write the expression for the equilibrium constant, $K_{c}$ for each of the following
Write the expression for the equilibrium constant, $K_{c}$ for each of the following
reactions:
(i) $2 \mathrm{NOCl}(\mathrm{g}) \longleftrightarrow 2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl}_{2}(\mathrm{~g})$
(ii) $2 \mathrm{Cu}\left(\mathrm{NO}_{3}\right)_{2}(\mathrm{~s}) \longleftrightarrow 2 \mathrm{CuO}(\mathrm{s})$
$+4 \mathrm{NO}_{2}(\mathrm{~g})+\mathrm{O}_{2}(\mathrm{~g})$
(iii) $\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}(\mathrm{aq})+\mathrm{H}_{2} \mathrm{O}(\mathrm{l}) \longleftrightarrow$
$\mathrm{CH}_{3} \mathrm{COOH}(\mathrm{aq})+\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}(\mathrm{aq})$
(iv) $\mathrm{Fe}^{3+}(\mathrm{aq})+3 \mathrm{OH}^{-}(\mathrm{aq}) \longleftrightarrow \mathrm{Fe}(\mathrm{OH})_{3}(\mathrm{~s})$
(v) $\mathrm{I}_{2}(\mathrm{~s})+5 \mathrm{~F}_{2} \longleftrightarrow 2 \mathrm{IF}_{5}$
Solution.(i)$K_{c}=\frac{\left[\mathrm{NO}_{(g)}\right]^{2}\left[\mathrm{Cl}_{2(g)}\right]}{\left[\mathrm{NOCl}_{(g)}\right]^{2}}$
(ii) $\quad K_{c}=\frac{\left[\mathrm{CuO}_{(s)}\right]^{2}\left[\mathrm{NO}_{2(g)}\right]^{4}\left[\mathrm{O}_{2(g)}\right]}{\left[\mathrm{Cu}\left(\mathrm{NO}_{3}\right)_{2(s)}\right]^{2}}$
$=\left[\mathrm{NO}_{2(g)}\right]^{4}\left[\mathrm{O}_{2(g)}\right]$
(iii) $K_{c}=\frac{\left[\mathrm{CH}_{3} \mathrm{COOH}_{(a q)}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}_{(a q)}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5(a q)}\right]\left[\mathrm{H}_{2} \mathrm{O}_{(t)}\right]}$
$=\frac{\left[\mathrm{CH}_{3} \mathrm{COOH}_{(a q)}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}_{(a q)}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5(a q)}\right]}$
(iv) $K_{c}=\frac{\left[\mathrm{Fe}(\mathrm{OH})_{3(s)}\right]}{\left[\mathrm{Fe}_{(a g)}\right]\left[\mathrm{OH}_{(a q)}^{-}\right]^{3+}}$
$=\frac{1}{\left[\mathrm{Fe}^{3+}{ }_{(o q)}\right]\left[\mathrm{OH}_{(a q)}^{-}\right]^{3}}$
(v)$K_{c}=\frac{\left[\mathrm{IF}_{5}\right]^{2}}{\left[\mathrm{I}_{2(s)}\right]\left[\mathrm{F}_{2}\right]^{5}}$
$=\frac{\left[\mathrm{IF}_{5}\right]^{2}}{\left[\mathrm{~F}_{2}\right]^{5}}$
Question 5: Find out the value of $K_{c}$ for each of the following equilibria from the value of $K_{p}$ :
(i) $2 \mathrm{NOCl}(\mathrm{g}) \longleftrightarrow 2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl}_{2}(\mathrm{~g})$;
$K_{p}=1.8 \times 10^{-2}$ at $500 \mathrm{~K}$
(ii) $\mathrm{CaCO}_{3}(\mathrm{~s}) \longleftrightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g}) ;$
$\mathrm{K}_{p}=167$ at $1073 \mathrm{~K}$
Solution. The relation between $K_{p}$ and $K_{c}$ is given as:
$K_{p}=K_{c}(\mathrm{RT})^{\Delta n}$
(a) Here,
$\Delta n=3-2=1$
$R=0.0831$ barLmol $^{-1} \mathrm{~K}^{-1}$
$T=500 \mathrm{~K}$
$K_{p}=1.8 \times 10^{-2}$
Now,
$K_{p}=K_{c}(R T)^{\Delta n}$
$\Rightarrow 1.8 \times 10^{-2}=K_{c}(0.0831 \times 500)^{1}$
$\Rightarrow K_{c}=\frac{1.8 \times 10^{-2}}{0.0831 \times 500}$
$=4.33 \times 10^{-4}$ (approximately)
(b) Here,
$\Delta n=2-1=1$
$R=0.0831$ barLmol $^{-1} K^{-1}$
$T=1073 \mathrm{~K}$
$K_{p}=167$
Now,
$K_{p}=K_{c}(R T)^{\Delta n}$
$\Rightarrow 167=K_{c}(0.0831 \times 1073)^{\Delta n}$
$\Rightarrow K_{c}=\frac{167}{0.0831 \times 1073}$
$=1.87$ (approximately)
Question 6: For the following equilibrium, $K_{\mathrm{C}}=6.3 \times 10^{14}$ at $1000 \mathrm{~K}$
$\mathrm{NO}(\mathrm{g})+\mathrm{O}_{3}(\mathrm{~g}) \longleftrightarrow \mathrm{NO}_{2}(\mathrm{~g})+\mathrm{O}_{2}(\mathrm{~g})$
Both the forward and reverse reactions in the equilibrium are elementary bimolecular reactions. What is $K_{c}$, for the reverse reaction?
Solution. It is given that $K_{C}$ for the forward reaction is $6.3 \times 10^{14}$.
Then, $K_{C}$ for the reverse reaction will be,
$K_{C}^{\prime}=\frac{1}{K_{C}}$
$=\frac{1}{6.3 \times 10^{14}}$
$=1.59 \times 10^{-15}$
Question 7: Explain why pure liquids and solids can be ignored while writing the equilibrium constant expression?
Solution. For a pure substance (both solids and liquids),
[Pure substance $]=\frac{\text { Number of moles }}{\text { Volume }}$
$=\frac{\text { Mass/molecular mass }}{\text { Volume }}$
$=\frac{\text { Mass }}{\text { Volume } \times \text { Molecular mass }}$
$=\frac{\text { Density }}{\text { Molecular mass }}$
Now, the molecular mass and density (at a particular temperature) of a pure substance is always fixed and is accounted for in the equilibrium constant. Therefore, the values of pure substances are not mentioned in the equilibrium constant expression.
Question 8: Reaction between $\mathrm{N}_{2}$ and $\mathrm{O}_{2}$ takes place as follows:
$2 \mathrm{~N}_{2}(\mathrm{~g})+\mathrm{O}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{~N}_{2} \mathrm{O}(\mathrm{g})$
If a mixture of $0.482$ mol of $\mathrm{N}_{2}$ and $0.933 \mathrm{~mol}$ of $\mathrm{O}_{2}$ is placed in a $10 \mathrm{~L}$ reaction vessel and allowed to form $\mathrm{N}_{2} \mathrm{O}$ at a temperature for which $K_{c}=2.0 \times 10^{-37}$, determine the composition of equilibrium mixture.
Solution. Let the concentration of $\mathrm{N}_{2} \mathrm{O}$ at equilibrium be $x$.
The given reaction is:
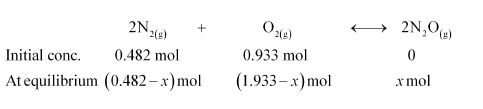
Therefore, at equilibrium, in the $10 \mathrm{~L}$ vessel:
$\left[\mathrm{N}_{2}\right]=\frac{0.482-x}{10},\left[\mathrm{O}_{2}\right]$
$=\frac{0.933-x / 2}{10},\left[\mathrm{~N}_{2} \mathrm{O}\right]=\frac{x}{10}$
The value of equilibrium constant i.e., $K_{c}=2.0 \times 10^{-37}$ is very small. Therefore, the amount of $\mathrm{N}_{2}$ and $\mathrm{O}_{2}$ reacted is also very small. Thus, $x$ can be neglected from the expressions of molar concentrations of $\mathrm{N}_{2}$ and $\mathrm{O}_{2}$
Then,
$\left[\mathrm{N}_{2}\right]=\frac{0.482}{10}=0.0482 \mathrm{~mol} \mathrm{~L}^{-1}$
and $\left[\mathrm{O}_{2}\right]=\frac{0.933}{10}=0.0933 \mathrm{~mol} \mathrm{~L}^{-1}$
Now.
$K_{\mathrm{C}}=\frac{\left[\mathrm{N}_{2} \mathrm{O}_{(\mathrm{g})}\right]^{2}}{\left[\mathrm{~N}_{2(\mathrm{~g})}\right]^{2}\left[\mathrm{O}_{2(\mathrm{~g})}\right]}$
$\Rightarrow 2.0 \times 10^{-37}=\frac{\left(\frac{x}{10}\right)^{2}}{(0.0482)^{2}(0.0933)}$
$\Rightarrow \frac{x^{2}}{100}=2.0 \times 10^{-37} \times(0.0482)^{2} \times(0.0933)$
$\Rightarrow x^{2}=43.35 \times 10^{-40}$
$\Rightarrow x=6.6 \times 10^{-20}$
$\left[\mathrm{N}_{2} \mathrm{O}\right]=\frac{x}{10}=\frac{6.6 \times 10^{-20}}{10}$
$=6.6 \times 10^{-21}$
Question 9: Nitric oxide reacts with $\mathrm{Br}_{2}$ and gives nitrosyl bromide as per reaction given below:
$2 \mathrm{NO}(\mathrm{g})+\mathrm{Br}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{NOBr}(\mathrm{g})$
When $0.087$ mol of NO and $0.0437$ mol of $\mathrm{Br}_{2}$ are mixed in a closed container at constant temperature, $0.0518$ mol of NOBr is obtained at equilibrium. Calculate equilibrium amount of $\mathrm{NO}$ and $\mathrm{Br}_{2}$.
Solution. The given reaction is:

Now, 2 mol of NOBr are formed from 2 mol of NO. Therefore, $0.0518$ mol of NOBr are formed from $0.0518$ mol of NO.
Again, 2 mol of NOBr are formed from 1 mol of Br.
Therefore, $0.0518$ mol of $\mathrm{NOBr}$ are formed from $\frac{0.0518}{2}$ mol of $\mathrm{Br}$, or
$0.0259$ mol of NO.
The amount of NO and Br present initially is as follows:
$[\mathrm{NO}]=0.087 \mathrm{~mol}\left[\mathrm{Br}_{2}\right]=0.0437 \mathrm{~mol}$
Therefore, the amount of NO present at equilibrium is:
$[\mathrm{NO}]=0.087-0.0518$
$=0.0352 \mathrm{~mol}$
And, the amount of Br present at equilibrium is:
$\left[\mathrm{Br}_{2}\right]=0.0437-0.0259$
$=0.0178 \mathrm{~mol}$
Question 10: At $450 \mathrm{~K}, K_{\mathrm{p}}=2.0 \times 10^{10} / \mathrm{bar}$ for the given reaction at equilibrium.
$2 \mathrm{SO}_{2(g)}+\mathrm{O}_{2(g)} \longleftrightarrow 2 \mathrm{SO}_{3(g)}$
What is $K_{c}$ at this temperature?
Solution. For the given reaction,
$\Delta n=2-3=-1$
$T=450 \mathrm{~K}$
$R=0.0831$ bar $\mathrm{L}$ bar $\mathrm{K}^{-1} \mathrm{~mol}^{-1}$
$K_{\mathrm{p}}=2.0 \times 10^{10} \mathrm{bar}^{-1}$
We know that,
$K_{\mathrm{P}}=K_{\mathrm{C}}(R T) \Delta n$
$\Rightarrow 2.0 \times 10^{10} \mathrm{bar}^{-1}$
$=K_{C}\left(0.0831 \mathrm{~L} \mathrm{bar} \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 450 \mathrm{~K}\right)^{-1}$
$\Rightarrow K_{\mathrm{C}}=\frac{2.0 \times 10^{10} \mathrm{bar}^{-1}}{\left(0.0831 \mathrm{~L} \text { bar } \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 450 \mathrm{~K}\right)^{-1}}$
$=\left(2.0 \times 10^{10} \mathrm{bar}^{-1}\right)\left(0.0831 \mathrm{~L} \mathrm{bar} \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 450 \mathrm{~K}\right)$
$=74.79 \times 10^{10} \mathrm{~L} \mathrm{~mol}^{-1}$
$=7.48 \times 10^{11} \mathrm{~L} \mathrm{~mol}^{-1}$
$=7.48 \times 10^{11} \mathrm{M}^{-1}$
Question 11: A sample of $\mathrm{HI}_{(\mathrm{g})}$ is placed in flask at a pressure of $0.2 \mathrm{~atm}$. At equilibrium the partial pressure of $\mathrm{HI}_{(\mathrm{g})}$ is $0.04 \mathrm{~atm} .$ What is $K_{\mathrm{p}}$ for the given equilibrium?
$2 \mathrm{HI}(\mathrm{g}) \longleftrightarrow \mathrm{H}_{2}(\mathrm{~g})+\mathrm{I}_{2}(\mathrm{~g})$
Solution. The initial concentration of HI is $0.2$ atm. At equilibrium, it has a partial pressure of $0.04$ atm. Therefore, a decrease in the pressure of $\mathrm{Hl}$ is $0.2-0.04=0.16$. The given reaction is:

Therefore,
$K_{\mathrm{p}}=\frac{p_{\mathrm{H}_{2}} \times p_{\mathrm{I}_{2}}}{p_{\mathrm{HI}}^{2}}$
$=\frac{0.08 \times 0.08}{(0.04)^{2}}$
$=\frac{0.0064}{0.0016}$
$=4.0$
Hence, the value of $K_{\mathrm{p}}$ for the given equilibrium is $4.0$.
Question $12$ : A mixture of $1.57 \mathrm{~mol}$ of $\mathrm{N}_{2}, 1.92 \mathrm{~mol}$ of $\mathrm{H}_{2}$ and $8.13 \mathrm{~mol}$ of $\mathrm{NH}_{3}$ is introduced into a $20 \mathrm{~L}$ reaction vessel at $500 \mathrm{~K}$. At this temperature, the equilibrium constant, $K_{c}$ for the reaction $\mathrm{N}_{2}(\mathrm{~g})+3 \mathrm{H}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{NH}_{3}(\mathrm{~g})$ is $1.7 \times 10^{2}$
Is the reaction mixture at equilibrium? If not, what is the direction of the net reaction?
Solution. The given reaction is:
$\mathrm{N}_{2(\mathrm{~g})}+3 \mathrm{H}_{2(\mathrm{~g})} \longleftrightarrow 2 \mathrm{NH}_{3(\mathrm{~g})}$
The given concentration of various species is
$\left[\mathrm{N}_{2}\right]=\frac{1.57}{20} \mathrm{~mol} \mathrm{~L}^{-1}$
$\left[\mathrm{H}_{2}\right]=\frac{1.92}{20} \mathrm{~mol} \mathrm{~L}^{-}$
$\left[\mathrm{NH}_{3}\right]=\frac{8.13}{20} \mathrm{~mol} \mathrm{~L}^{-}$
Now, reaction quotient $Q_{c}$ is:
$Q_{\mathrm{C}}=\frac{\left[\mathrm{NH}_{3}\right]^{2}}{\left[\mathrm{~N}_{2}\right]\left[\mathrm{H}_{2}\right]^{3}}$
$=\frac{\left(\frac{(8.13)}{20}\right)^{2}}{\left(\frac{1.57}{20}\right)\left(\frac{1.92}{20}\right)^{3}}$
$=2.4 \times 10^{3}$
Since $Q_{\mathrm{C}} \neq K_{\mathrm{C}}$, the reaction mixture is not at equilibrium.
Again, $Q_{\mathrm{C}}>K_{\mathrm{c}}$. Hence, the reaction will proceed in the reverse direction.
Question 13: The equilibrium constant expression for a gas reaction is,
$K_{\mathrm{C}}=\frac{\left[\mathrm{NH}_{3}\right]^{4}\left[\mathrm{O}_{2}\right]^{5}}{[\mathrm{NO}]^{4}\left[\mathrm{H}_{2} \mathrm{O}\right]^{6}}$
Write the balanced chemical equation corresponding to this expression.
Solution. The balanced chemical equation corresponding to the given expression can be written as:
$4 \mathrm{NO}_{(g)}+6 \mathrm{H}_{2} \mathrm{O}_{(g)} \longleftrightarrow 4 \mathrm{NH}_{3(g)}+5 \mathrm{O}_{2(g)}$
Question 14:One mole of $\mathrm{H}_{2} \mathrm{O}$ and one mole of $\mathrm{CO}$ are taken in $10 \mathrm{~L}$ vessel and heated to
$725 \mathrm{~K}$. At equilibrium $40 \%$ of water (by mass) reacts with $\mathrm{CO}$ according to the equation,
$\mathrm{H}_{2} \mathrm{O}(\mathrm{g})+\mathrm{CO}(\mathrm{g}) \longleftrightarrow \mathrm{H}_{2}(\mathrm{~g})+\mathrm{CO}_{2}(\mathrm{~g})$
Calculate the equilibrium constant for the reaction.
Solution. The given reaction is:

Therefore, the equilibrium constant for the reaction,
$K_{\mathrm{C}}=\frac{\left[\mathrm{H}_{2}\right]\left[\mathrm{CO}_{2}\right]}{\left[\mathrm{H}_{2} \mathrm{O}\right][\mathrm{CO}]}$
$=\frac{0.04 \times 0.04}{0.06 \times 0.06}$
$=0.444$ (approximately)
Question $15$ : At $700 \mathrm{~K}$, equilibrium constant for the reaction
$\mathrm{H}_{2(g)}+\mathrm{I}_{2(g)} \longleftrightarrow 2 \mathrm{HI}_{(g)}$
is $54.8$. If $0.5 \mathrm{molL}^{-1}$ of $\mathrm{HI}_{(g)}$ is present at equilibrium at $700 \mathrm{~K}$, what are the concentration of $\mathrm{H}_{2(g)}$ and $\mathrm{I}_{2(g)}$ assuming that we initially started with $\mathrm{HI}_{(g)}$ and allowed it to reach equilibrium at $700 \mathrm{~K} ?$
Solution. It is given that equilibrium constant $K_{\mathrm{c}}$ for the reaction
$\mathrm{H}_{2(g)}+\mathrm{I}_{2(g)} \longleftrightarrow 2 \mathrm{HI}_{(g)}$ is $54.8$
Therefore, at equilibrium, the equilibrium constant $K_{\mathrm{c}}^{\prime}$ for the reaction
$2 \mathrm{HI}_{(\mathrm{g})} \longleftrightarrow \mathrm{H}_{2(\mathrm{~g})}+\mathrm{I}_{2(\mathrm{~g})}$ will be $\frac{1}{54.8} .$
$[\mathrm{HI}]=0.5 \mathrm{molL}^{-1}$
Let the concentrations of hydrogen and iodine at equilibrium be $x \mathrm{molL}^{-1}$
$\left[\mathrm{H}_{2}\right]=\left[\mathrm{I}_{2}\right]=x \mathrm{~mol} \mathrm{~L}^{-1}$
Therefore,
$\frac{\left[\mathrm{H}_{2}\right]\left[\mathrm{I}_{2}\right]}{[\mathrm{HI}]^{2}}=K_{\mathrm{C}}^{\prime}$
$\Rightarrow \frac{x \times x}{(0.5)^{2}}=\frac{1}{54.8}$
$\Rightarrow x^{2}=\frac{0.25}{54.8}$
$\Rightarrow x=0.06754$
$x=0.068 \mathrm{molL}^{-1}$ (approximately)
Hence, at equilibrium, $\left[\mathrm{H}_{2}\right]=\left[\mathrm{I}_{2}\right]=0.068 \mathrm{~mol} \mathrm{~L}^{-1}$.
Question 16: What is the equilibrium concentration of each of the substances in the equilibrium when the initial concentration of ICl was $0.78 \mathrm{M}$ ?
$2 \mathrm{Cl}(\mathrm{g}) \rightleftharpoons \mathrm{I}_{2}(\mathrm{~g})+\mathrm{Cl}_{2}(\mathrm{~g}) ; \mathrm{K}_{\mathrm{C}}=0.14$
Solution. The given reaction is:
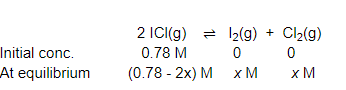
Now, we can write,
$\frac{\left[\mathrm{I}_{2}\right]\left[\mathrm{Cl}_{2}\right]}{[\mathrm{ICl}]^{2}}=K_{\mathrm{C}}$
$\Rightarrow \frac{x \times x}{(0.78-2 x)^{2}}=0.14$
$\Rightarrow \frac{x^{2}}{(0.78-2 x)^{2}}=0.14$
$\Rightarrow \frac{x}{0.78-2 x}=0.374$
$\Rightarrow x=0.292-0.748 x$
$\Rightarrow 1.748 x=0.292$
$\Rightarrow x=0.167$
Hence, at equilibrium,
$[\mathrm{ICl}]=\left[\mathrm{I}_{2}\right]=0.167 \mathrm{M}$
$[\mathrm{ICl}]=(0.78-2 \times 0.167) \mathrm{M}$
$=0.446 \mathrm{M}$
Question 17: $K_{\mathrm{p}}=0.04 \mathrm{~atm}$ at $899 \mathrm{~K}$ for the equilibrium shown below. What is the equilibrium concentration of $\mathrm{C}_{2} \mathrm{H}_{6}$ when it is placed in a flask at $4.0$ atm pressure and allowed to come to equilibrium?
Solution. Let $p$ be the pressure exerted by ethene and hydrogen gas (each) at equilibrium.
Now, according to the reaction,
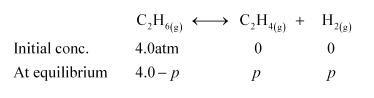
We can write,
$\frac{p_{\mathrm{C}_{2} \mathrm{H}_{4}} \times p_{\mathrm{H}_{2}}}{p_{\mathrm{C}_{2} \mathrm{H}_{6}}}=K_{p}$
$\Rightarrow \frac{p \times p}{4.0-p}=0.04$
$\Rightarrow p^{2}+0.16-0.04 p$
$\Rightarrow p^{2}+0.04 p-0.16=0$
Now, $p=\frac{-0.04 \pm \sqrt{(0.04)^{2}-4 \times 1 \times(-0.16)}}{2 \times 1}$
$=\frac{-0.04 \pm 0.80}{2}$
$=\frac{0.76}{2} \quad$ (Taking positive value) $=\frac{0.76}{2} \quad$ (Taking positive value)
$=0.38$
Hence, at equilibrium,
$\left[\mathrm{C}_{2} \mathrm{H}_{6}\right]-4-p=4-0.38$
$=3.62 \mathrm{~atm}$
Question 18: Ethyl acetate is formed by the reaction between ethanol and acetic acid and the equilibrium is represented as:
$\mathrm{CH}_{3} \mathrm{COOH}(\mathrm{l})+\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}$ ( 1$)$
$\longleftrightarrow \mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}$ (I) $+\mathrm{H}_{2} \mathrm{O}$ (I)
(i) Write the concentration ratio (reaction quotient), $Q \mathrm{c}$, for this reaction (note: water is not in excess and is not a solvent in this reaction)
(ii) At $293 \mathrm{~K}$, if one starts with $1.00 \mathrm{~mol}$ of acetic acid and $0.18 \mathrm{~mol}$ of ethanol, there is $0.171 \mathrm{~mol}$ of ethyl acetate in the final equilibrium mixture. Calculate the equilibrium constant.
(iii) Starting with $0.5 \mathrm{~mol}$ of ethanol and $1.0 \mathrm{~mol}$ of acetic acid and maintaining it at $293 \mathrm{~K}, 0.214$ mol of ethyl acetate is found after sometime. Has equilibrium been reached?
Solution. (i) Reaction quotient, $Q_{c}$
$=\frac{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}\right]}$
(ii) Let the volume of the reaction mixture be $V$. Also, here we will consider that water is a solvent and is present in excess.
The given reaction is:
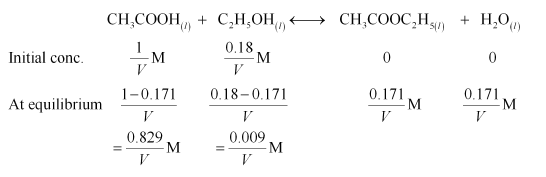
Therefore, equilibrium constant for the given reaction is:
$K_{\mathrm{C}}=\frac{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}\right]}$
$=\frac{\frac{0.171}{V} \times \frac{0.171}{V}}{\frac{0.829}{V} \times \frac{0.009}{V}}=3.919$
$=3.92$ (approximately)
(iii) Let the volume of the reaction mixture be $V$.
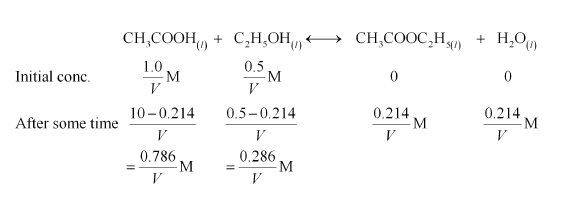
Therefore, the reaction quotient is,
$Q_{\mathrm{C}}=\frac{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}\right]}$
$=\frac{\frac{0.214}{V} \times \frac{0.214}{V}}{\frac{0.786}{V} \times \frac{0.286}{V}}$
$=0.2037$
$=0204$ (approximately)
Since $Q_{\mathrm{C}}
Question 19: A sample of pure $\mathrm{PCl}_{5}$ was introduced into an evacuated vessel at $473 \mathrm{~K}$. After equilibrium was attained, concentration of $\mathrm{PCl}_{5}$ was found to
be $0.5 \times 10^{-1} \mathrm{~mol} \mathrm{~L}^{-1}$. If value of $K_{c}$ is $8.3 \times 10^{-3}$, what are the concentrations of $\mathrm{PCl}_{3}$ and $\mathrm{Cl}_{2}$ at equilibrium?
$\mathrm{PCl}_{5}(\mathrm{~g}) \longleftrightarrow \mathrm{PCl}_{3}(\mathrm{~g})+\mathrm{Cl}_{2}(\mathrm{~g})$
Solution. Let the concentrations of both $\mathrm{PCl}_{3}$ and $\mathrm{Cl}_{2}$ at equilibrium be $x \mathrm{moll}^{-1}$. The given reaction is:

It is given that the value of equilibrium constant, $K_{\mathrm{C}}$ is $8.3 \times 10^{-3}$.
Now we can write the expression for equilibrium as:
$\frac{\left[\mathrm{PCl}_{2}\right]\left[\mathrm{Cl}_{2}\right]}{\left[\mathrm{PCl}_{5}\right]}=K_{\mathrm{C}}$
$\Rightarrow \frac{x \times x}{0.5 \times 10^{-1}}=8.3 \times 10^{-3}$
$\Rightarrow x^{2}=4.15 \times 10^{-4}$
$\Rightarrow x=2.04 \times 10^{-2}$
$=0.0204$
$=0.02$ (approximately)
Therefore, at equilibrium,
$\left[\mathrm{PCl}_{3}\right]=\left[\mathrm{Cl}_{2}\right]=0.02 \mathrm{~mol} \mathrm{~L}^{-1} .$
Question 20: One of the reactions that takes place in producing steel from iron ore is the reduction of iron (II) oxide by carbon monoxide to give iron metal and $\mathrm{CO}_{2}$
$\mathrm{FeO}(\mathrm{s})+\mathrm{CO}(\mathrm{g}) \longleftrightarrow \mathrm{Fe}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g})$
$K_{p}=0.265$ at $1050 \mathrm{~K}$
What are the equilibrium partial pressures of $\mathrm{CO}$ and $\mathrm{CO}_{2}$ at $1050 \mathrm{~K}$ if the initial partial pressures are: $p_{\mathrm{co}}=1.4 \mathrm{~atm}$ and $p_{\mathrm{CO}_{2}}=0.80 \mathrm{~atm} ?$
Solution. For the given reaction,
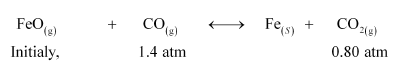
$Q_{\mathrm{P}}=\frac{p_{\mathrm{CO}_{2}}}{p_{\mathrm{CO}}}$
$=\frac{0.80}{1.4}$
$=0.571$
It is given that $K_{\mathrm{p}}=0.265$.
Since $Q_{\mathrm{p}}>K_{\mathrm{p}}$, the reaction will proceed in the backward direction.
Therefore, we can say that the pressure of CO will increase while the pressure of $\mathrm{CO}_{2}$ will decrease.
Now, let the increase in pressure of $\mathrm{CO}=$ decrease in pressure of $\mathrm{CO}_{2}$ be $p$
Then, we can write,
$K_{\mathrm{P}}=\frac{p_{\mathrm{CO}_{2}}}{p_{\mathrm{CO}}}$
$\Rightarrow 0.265=\frac{0.80-p}{1.4+p}$
$\Rightarrow 0.371+0.265 p=0.80-p$
$\Rightarrow 1.265 p=0.429$
$\Rightarrow p=0.339 \mathrm{~atm}$
Therefore, equilibrium partial of $\mathrm{CO}_{2}, p_{\mathrm{co}}$
$=0.80-0.339=0.461 \mathrm{~atm}$
And, equilibrium partial pressure of $\mathrm{CO}, p_{\mathrm{co}}$
$=1.4+0.339=1.739 \mathrm{~atm} .$
Question 21: Equilibrium constant, $K_{c}$ for the reaction
$\mathrm{N}_{2}(\mathrm{~g})+3 \mathrm{H}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{NH}_{3}(\mathrm{~g})$ at $500 \mathrm{~K}$ is $0.061$
At a particular time, the analysis shows that composition of the reaction mixture is $3.0 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~N}_{2}, 2.0 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{H}_{2}$ and $0.5 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{NH}_{3}$. Is the reaction at equilibrium? If not in which direction does the reaction tend to proceed to reach equilibrium?
Solution. The given reaction is:
$\mathrm{N}_{2(\mathrm{~g})}+3 \mathrm{H}_{2(\mathrm{~g})} \longleftrightarrow \quad 2 \mathrm{NH}_{3(\mathrm{~g})}$
At a particular time: $3.0 \mathrm{~mol} \mathrm{~L}^{-1} \quad 2.0 \mathrm{~mol} \mathrm{~L}^{-1}$ $0.5 \mathrm{~mol} \mathrm{~L}^{-1}$
Now, we know that,
$Q_{\mathrm{C}}=\frac{\left[\mathrm{NH}_{3}\right]^{2}}{\left[\mathrm{~N}_{2}\right]\left[\mathrm{H}_{2}\right]^{3}}$
$=\frac{(0.5)^{2}}{(3.0)(2.0)^{3}}$
$=0.0104$
It is given that $K_{\mathrm{C}}=0.061$.
Since $Q_{\mathrm{C}} \neq K_{\mathrm{c}}$, the reaction is not at equilibrium.
Since $Q_{\mathrm{C}}
Question 22: Bromine monochloride, $\mathrm{BrCl}$ decomposes into bromine and chlorine and reaches the equilibrium:
$2 \mathrm{BrCl}(\mathrm{g}) \longleftrightarrow \mathrm{Br}_{2}(\mathrm{~g})+\mathrm{Cl}_{2}(\mathrm{~g})$
for which $K_{c}=32$ at $500 \mathrm{~K}$. If initially pure $\mathrm{BrCl}$ is present at a concentration of $3.3 \times 10^{-3} \mathrm{molL}^{-1}$, what is its molar concentration in the mixture at equilibrium?
Solution. Let the amount of bromine and chlorine formed at equilibrium be $x$. The given reaction is:

Now, we can write,
$\frac{\left[\mathrm{Br}_{2}\right]\left[\mathrm{Cl}_{2}\right]}{[\mathrm{BrCl}]^{2}}=K_{\mathrm{C}}$
$\Rightarrow \frac{x \times x}{\left(3.3 \times 10^{-3}-2 x\right)^{2}}=32$
$\Rightarrow \frac{x}{3.3 \times 10^{-3}-2 x}=5.66$
$\Rightarrow x=18.678 \times 10^{-3}-11.32 x$
$\Rightarrow 12.32 x=18.678 \times 10^{-3}$
$\Rightarrow x=1.5 \times 10^{-3}$
Therefore, at equilibrium,
$[\mathrm{BrCl}]=3.3 \times 10^{-3}-\left(2 \times 1.5 \times 10^{-3}\right)$
$=3.3 \times 10^{-3}-3.0 \times 10^{-3}$
$=0.3 \times 10^{-3}$
$=3.0 \times 10^{-4} \mathrm{molL}^{-1}$
Question 23: At $1127 \mathrm{~K}$ and 1 atm pressure, a gaseous mixture of $\mathrm{CO}$ and $\mathrm{CO}_{2}$ in equilibrium with solid carbon has $90.55 \%$ CO by mass
$\mathrm{C}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{CO}(\mathrm{g})$
Calculate $K_{c}$ for this reaction at the above temperature.
Solution. Let the total mass of the gaseous mixture be $100 \mathrm{~g}$.
Mass of $\mathrm{CO}=90.55 \mathrm{~g}$
And, mass of $\mathrm{CO}_{2}=(100-90.55)=9.45 \mathrm{~g}$
Now, number of moles of $\mathrm{CO}$
$n_{\mathrm{CO}}=\frac{90.55}{28}=3.234 \mathrm{~mol}$
Number of moles of $\mathrm{CO}_{2}$
$n_{\mathrm{CO}_{2}}=\frac{9.45}{44}=0.215 \mathrm{~mol}$
Partial pressure of $\mathrm{CO}$
$p_{\mathrm{CO}}=\frac{n_{\mathrm{CO}}}{n_{\mathrm{CO}}+n_{\mathrm{CO}_{2}}} \times p_{\text {total }}$
$=\frac{3.234}{3.234+0.215} \times 1$
$=0.938 \mathrm{~atm}$
Partial pressure of $\mathrm{CO}_{2}$
$p_{\mathrm{CO}_{2}}=\frac{n_{\mathrm{CO}_{2}}}{n_{\mathrm{CO}}+n_{\mathrm{CO}_{2}}} \times p_{\text {tocal }}$
$=\frac{0.215}{3.234+0.215} \times 1$
$=0.062 \mathrm{~atm}$
Therefore, $K_{\mathrm{p}}=\frac{[\mathrm{CO}]^{2}}{\left[\mathrm{CO}_{2}\right]}$
$=\frac{(0.938)^{2}}{0.062}$
$=14.19$
For the given reaction,
$\Delta n=2-1=1$
We know that,
$K_{\mathrm{P}}=K_{\mathrm{C}}(R T)^{\mathrm{N}}$
$\Rightarrow 14.19=K_{\mathrm{C}}(0.082 \times 1127)^{\prime}$
$\Rightarrow K_{\mathrm{C}}=\frac{14.19}{0.082 \times 1127}$
$=0.154($ approximately $)$
Question 24: Calculate
a) $\Delta G^{\circ}$ and $b$ ) the equilibrium constant for the formation of $\mathrm{NO}_{2}$ from $\mathrm{NO}$ and $\mathrm{O}_{2}$ at $298 \mathrm{~K}$
$\mathrm{NO}(\mathrm{g})+1 / 2 \mathrm{O}_{2}(\mathrm{~g}) \longleftrightarrow \mathrm{NO}_{2}(\mathrm{~g})$
where $\Delta_{f} G^{\circ}\left(\mathrm{NO}_{2}\right)=52.0 \mathrm{~kJ} / \mathrm{mol}$
$\Delta_{f} G^{\circ}(\mathrm{NO})=87.0 \mathrm{~kJ} / \mathrm{mol}$
$\Delta_{f} \mathrm{G}^{\circ}\left(\mathrm{O}_{2}\right)=0 \mathrm{~kJ} / \mathrm{mol}$
Solution. (a) For the given reaction,
$\Delta G^{\circ}=\Delta G^{\circ}($ Products $)-\Delta G^{\circ}($ Reactants $)$
$\Delta G^{\circ}=52.0-\{87.0+0\}$
$=-35.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$
(b) We know that,
$\Delta G^{\circ}=R T \log K_{c}$
$\Delta G^{\circ}=2.303 \mathrm{RT} \log K_{c}$
$K_{c}=\frac{-35.0 \times 10^{-3}}{-2.303 \times 8.314 \times 298}$
$=6.134$
$\therefore K_{c}=$ antilog $(6.134)$
$=1.36 \times 10^{6}$
Hence, the equilibrium constant for the given reaction $K_{c}$ is $1.36 \times 10^{6}$
Question $25$ : Does the number of moles of reaction products increase, decrease or remain same when each of the following equilibria is subjected to a decrease in pressure by increasing the volume?
(a) $\mathrm{PCl}_{5}(\mathrm{~g}) \longleftrightarrow \mathrm{PCl}_{3}(\mathrm{~g})+\mathrm{Cl}_{2}$ (g)
(b) $\mathrm{CaO}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g}) \longleftrightarrow \mathrm{CaCO}_{3}(\mathrm{~s})$
(c) $3 \mathrm{Fe}(\mathrm{s})+4 \mathrm{H}_{2} \mathrm{O}(\mathrm{g}) \longleftrightarrow \mathrm{Fe}_{3} \mathrm{O}_{4}(\mathrm{~s})+4 \mathrm{H}_{2}(\mathrm{~g})$
Solution. (a) The number of moles of reaction products will increase. According to Le Chatelier's principle, if pressure is decreased, then the equilibrium shifts in the direction in which the number of moles of gases is more. In the given reaction, the number of moles of gaseous products is more than that of gaseous reactants. Thus, the reaction will proceed in the forward direction. As a result, the number of moles of reaction products will increase.
(b) The number of moles of reaction products will decrease.
(c) The number of moles of reaction products remains the same.
Question 26: Which of the following reactions will get affected by increasing the pressure?
Also, mention whether change will cause the reaction to go into forward or backward direction.
(i) $\mathrm{COCl}_{2}(\mathrm{~g}) \longleftrightarrow \mathrm{CO}(\mathrm{g})+\mathrm{Cl}_{2}(\mathrm{~g})$
(ii) $\mathrm{CH}_{4}(\mathrm{~g})+2 \mathrm{~S}_{2}$$(\mathrm{g}) \longleftrightarrow \mathrm{CS}_{2}(\mathrm{~g})+2 \mathrm{H}_{2} \mathrm{~S}(\mathrm{~g})$
(iii) $\mathrm{CO}_{2}(\mathrm{~g})+\mathrm{C}(\mathrm{s}) \longleftrightarrow 2 \mathrm{CO}(\mathrm{g})$
(iv) $2 \mathrm{H}_{2}(\mathrm{~g})+\mathrm{CO}(\mathrm{g}) \longleftrightarrow \mathrm{CH}_{3} \mathrm{OH}(\mathrm{g})$
(v) $\mathrm{CaCO}_{3}(\mathrm{~s}) \longleftrightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g})$
(vi) $4 \mathrm{NH}_{3}(\mathrm{~g})+5 \mathrm{O}_{2}(\mathrm{~g}) \longleftrightarrow 4 \mathrm{NO}(\mathrm{g})+6 \mathrm{H}_{2} \mathrm{O}(\mathrm{g})$
Solution. The reactions given in (i), (iii), (iv), (v), and (vi) will get affected by increasing the pressure.
The reaction given in (iv) will proceed in the forward direction because the number of moles of gaseous reactants is more than that of gaseous products.
The reactions given in (i), (iii), (v), and (vi) will shift in the backward direction because the number of moles of gaseous reactants is less than that of gaseous products.
Question 27: The equilibrium constant for the following reaction is $1.6 \times 10^{5}$ at $1024 \mathrm{~K}$.
$\mathrm{H}_{2}(\mathrm{~g})+\mathrm{Br}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{HBr}(\mathrm{g})$strong>
Find the equilibrium pressure of all gases if $10.0$ bar of $\mathrm{HBr}$ is introduced into a sealed container at $1024 \mathrm{~K}$.
Solution. Given.
$K_{p}$ for the reaction i.e., $\mathrm{H}_{2(\mathrm{~g})}$
$+\mathrm{Br}_{2(g)} \longleftrightarrow 2 \mathrm{HBr}_{(\mathrm{g})}$ is $1.6 \times 10^{5}$
Therefore, for the reaction $2 \mathrm{HBr}_{(\mathrm{g})} \longleftrightarrow \mathrm{H}_{2(\mathrm{~g})}$
$+\mathrm{Br}_{2(\mathrm{~g})}$, the equilibrium constant will be,
$K_{\mathrm{p}}^{\prime}=\frac{1}{K_{\mathrm{P}}}$
$=\frac{1}{1.6 \times 10^{5}}$
$=6.25 \times 10^{-6}$
Now, let $p$ be the pressure of both $\mathrm{H}_{2}$ and $\mathrm{Br}_{2}$ at equilibrium.

Now, we can write,
$\frac{p_{\mathrm{HB}_{1}} \times p_{2}^{\times}}{p_{\mathrm{HBr}}^{2}}=K_{\mathrm{P}}^{\prime}$
$\frac{p \times p}{(10-2 p)^{2}}=6.25 \times 10^{-6}$
$\frac{p}{10-2 p}=2.5 \times 10^{-3}$
$p=2.5 \times 10^{-2}-\left(5.0 \times 10^{-3}\right) p$
$p+\left(5.0 \times 10^{-3}\right) p=2.5 \times 10^{-2}$
$\left(1005 \times 10^{-3}\right) p=2.5 \times 10^{-2}$
$p=2.49 \times 10^{-2}$ bar $=2.5 \times 10^{-2}$ bar (approximately)
Therefore, at equilibrium,
$\left[\mathrm{H}_{2}\right]=\left[\mathrm{Br}_{2}\right]=2.49 \times 10^{-2} \mathrm{bar}$
$[\mathrm{HBr}]=10-2 \times\left(2.49 \times 10^{-2}\right) \mathrm{bar}$
$=9.95 \mathrm{bar}=10 \mathrm{bar}($ approximately $)$
Question $28:$ Dihydrogen gas is obtained from natural gas by partial oxidation with steam as per following endothermic reaction:
$\mathrm{CH}_{4}(\mathrm{~g})+\mathrm{H}_{2} \mathrm{O}(\mathrm{g}) \longleftrightarrow \mathrm{CO}(\mathrm{g})+3 \mathrm{H}_{2}(\mathrm{~g})$
(a) Write as expression for $K_{p}$ for the above reaction.
(b) How will the values of $K_{p}$ and composition of equilibrium mixture be affected by
(i) Increasing the pressure
(ii) Increasing the temperature
(iii) Using a catalyst?
Solution. (a) For the given reaction,
$K_{P}=\frac{p_{\mathrm{CO}} \times p_{\mathrm{H}_{2}}^{3}}{p_{\mathrm{CH}_{4}} \times p_{\mathrm{H}_{2} \mathrm{O}}}$
(b) (i) According to Le Chatelier's principle, the equilibrium will shift in the backward direction.
(ii) According to Le Chatelier's principle, as the reaction is endothermic, the equilibrium will shift in the forward direction.
(iii) The equilibrium of the reaction is not affected by the presence of a catalyst. A catalyst only increases the rate of a reaction. Thus, equilibrium will be attained quickly.
Question 29: Describe the effect of:
a) Addition of $\mathrm{H}_{2}$
b) Addition of $\mathrm{CH}_{3} \mathrm{OH}$
c) Removal of $\mathrm{CO}$
d) Removal of $\mathrm{CH}_{3} \mathrm{OH}$
on the equilibrium of the reaction:
$2 \mathrm{H}_{2}(\mathrm{~g})+\mathrm{CO}(\mathrm{g}) \longleftrightarrow \mathrm{CH}_{3} \mathrm{OH}(\mathrm{g})$
Solution. (a) According to Le Chatelier's principle, on addition of $\mathrm{H}_{2}$, the equilibrium of the given reaction will shift in the forward direction.
(b) On addition of $\mathrm{CH}_{3} \mathrm{OH}$, the equilibrium will shift in the backward direction.
(c) On removing CO, the equilibrium will shift in the backward direction.
(d) On removing $\mathrm{CH}_{3} \mathrm{OH}$, the equilibrium will shift in the forward direction.
Question 30: At $473 \mathrm{~K}$, equilibrium constant $K_{c}$ for decomposition of phosphorus pentachloride, $\mathrm{PCl}_{5}$ is $8.3 \times 10^{-3}$. If decomposition is depicted as,
$\mathrm{PCl}_{5}(\mathrm{~g}) \longleftrightarrow \mathrm{PCl}_{3}(\mathrm{~g})+\mathrm{Cl}_{2}(\mathrm{~g})$
(g) $\Delta_{r} H^{\circ}=124.0 \mathrm{kJmol}^{-1}$
a) Write an expression for $K_{c}$ for the reaction.
b) What is the value of $K_{c}$ for the reverse reaction at the same temperature?
c) What would be the effect on $K_{c}$ if (i) more $\mathrm{PCl}_{5}$ is added (ii) pressure is increased? (iii) The temperature is increased?
Solution. (a) $K_{c} \frac{\left[\mathrm{PCl}_{3(\mathrm{~g})}\right]\left[\mathrm{Cl}_{2(\mathrm{~g})}\right]}{\left[\mathrm{PCl}_{5(\mathrm{~g})}\right]}$
(b) Value of $K_{c}$ for the reverse reaction at the same temperature is:
$K_{c}^{\prime}=\frac{1}{K_{c}}$
$=\frac{1}{8.3 \times 10^{-3}}=1.2048 \times 10^{2}$
$=120-48$
(c) (i) $K_{c}$ would remain the same because in this case, the temperature remains the same.
(ii) $K_{c}$ is constant at constant temperature. Thus, in this case, $K_{c}$ would not change.
(iii) In an endothermic reaction, the value of $K_{c}$ increases with an increase in temperature. Since the given reaction in an endothermic reaction, the value of $K_{c}$ will increase if the temperature is increased.
Question 31: Dihydrogen gas used in Haber's process is produced by reacting methane from natural gas with high temperature steam. The first stage of two stage reaction involves the formation of $\mathrm{CO}$ and $\mathrm{H}_{2}$. In second stage, $\mathrm{CO}$ formed in first stage is reacted with more steam in water gas shift reaction,
$\mathrm{CO}(\mathrm{g})+\mathrm{H}_{2} \mathrm{O}(\mathrm{g}) \longleftrightarrow \mathrm{CO}_{2}(\mathrm{~g})+\mathrm{H}_{2}(\mathrm{~g})$
If a reaction vessel at $400^{\circ} \mathrm{C}$ is charged with an equimolar mixture of $\mathrm{CO}$ and steam such that $p_{\mathrm{CO}}=p_{\mathrm{H}_{2} \mathrm{O}}=4.0 \mathrm{bar}$, what will be the partial pressure of $\mathrm{H}_{2}$ at equilibrium? $\mathrm{Kp}=10.1$ at $400^{\circ} \mathrm{C}$
Solution. Let the partial pressure of both carbon dioxide and hydrogen gas be $p$. The given reaction is:
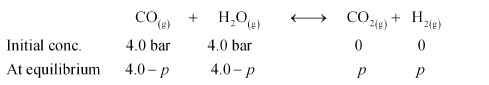
It is given that $K_{\mathrm{p}}=10.1$.
Now,
$\frac{p_{\mathrm{CO}_{2}} \times p_{\mathrm{H}_{2}}}{p_{\mathrm{CO}+} \times \mathrm{P}_{2}}=K_{\mathrm{P}}$
$\Rightarrow \frac{p \times p}{(4.0-p)(4.0-p)}=10.1$
$\Rightarrow \frac{p}{4.0-p}=3.178$
$\Rightarrow p=12.712-3.178 p$
$\Rightarrow 4.178 p=12.712$
$\Rightarrow p=3.04$
Hence, at equilibrium, the partial pressure of $\mathrm{H}_{2}$ will be $3.04$ bar.
Question $32$ : Predict which of the following reaction will have appreciable concentration of reactants and products:
a) $\mathrm{Cl}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{Cl}(\mathrm{g}) ; \quad K_{c}=5 \times 10^{-39}$
$K_{c}=3.7 \times 10^{8}$
b) $\mathrm{Cl}_{2}(\mathrm{~g})+2 \mathrm{NO}(\mathrm{g}) \longleftrightarrow 2 \mathrm{NOCl}(\mathrm{g})$;
$K_{c}=3.7 \times 10^{8}$
c) $\mathrm{Cl}_{2}(\mathrm{~g})+2 \mathrm{NO}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{NO}_{2} \mathrm{Cl}(\mathrm{g})$;
$K_{c}=1.8$
Solution. If the value of $K_{c}$ lies between $10^{-3}$ and $10^{3}$, a reaction has appreciable concentration of reactants and products. Thus, the reaction given in (c) will have appreciable concentration of reactants and products.
Question $33$ : The value of $K_{c}$ for the reaction
$3 \mathrm{O}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{O}_{3}(\mathrm{~g})$
is $2.0 \times 10^{-50}$ at $25^{\circ} \mathrm{C}$. If the equilibrium concentration of $\mathrm{O}_{2}$ in air at $25^{\circ} \mathrm{C}$ is $1.6 \times 10^{-2}$, what is the concentration of $\mathrm{O}_{3} ?$
Solution. The given reaction is:
$3 \mathrm{O}_{2(\mathrm{~g})} \longleftrightarrow 2 \mathrm{O}_{3(\mathrm{~g})}$
Then,
$K_{C}=\frac{\left[\mathrm{O}_{3(\mathrm{~g})}\right]^{2}}{\left[\mathrm{O}_{2(\mathrm{~g})}\right]^{3}}$
It is given that $K_{\mathrm{C}}=2.0 \times 10^{-50}$
and $\left[\mathrm{O}_{2(\mathrm{~g})}\right]=1.6 \times 10^{-2}$.
Then, we have,
$2.0 \times 10^{-50}=\frac{\left[\mathrm{O}_{3(\mathrm{~g})}\right]^{2}}{\left[1.6 \times 10^{-2}\right]^{3}}$
$\Rightarrow\left[\mathrm{O}_{3(\mathrm{~g})}\right]^{2}=2.0 \times 10^{-50} \times\left(1.6 \times 10^{-2}\right)^{3}$
$\Rightarrow\left[\mathrm{O}_{3(\mathrm{~g})}\right]^{2}=8.192 \times 10^{-56}$
$\Rightarrow\left[\mathrm{O}_{3(\mathrm{~g})}\right]=2.86 \times 10^{-28} \mathrm{M}$
Hence, the concentration of $\mathrm{O}_{3}$ is $2.86 \times 10^{-28} \mathrm{M}$.
Question 34: The reaction, $\mathrm{CO}(\mathrm{g})+3 \mathrm{H}_{2}(\mathrm{~g}) \longleftrightarrow \mathrm{CH}_{4}(\mathrm{~g})+\mathrm{H}_{2} \mathrm{O}(\mathrm{g})$ is at equilibrium at $1300 \mathrm{~K}$ in a $1 \mathrm{~L}$ flask. It also contain $0.30 \mathrm{~mol}$ of $\mathrm{CO}, 0.10 \mathrm{~mol}$ of $\mathrm{H}_{2}$ and $0.02 \mathrm{~mol}$ of $\mathrm{H}_{2} \mathrm{O}$ and an unknown amount of $\mathrm{CH}_{4}$ in the flask. Determine the concentration of $\mathrm{CH}_{4}$ in the mixture. The equilibrium constant, $K_{c}$ for the reaction at the given temperature is $3.90$.
Solution. Let the concentration of methane at equilibrium be $x$.

It is given that $K_{c}=3.90$.
Therefore,
$\frac{\left[\mathrm{CH}_{4(\mathrm{~g})}\right]\left[\mathrm{H}_{2} \mathrm{O}_{(\mathrm{g})}\right]}{\left[\mathrm{CO}_{(\mathrm{g})}\right]\left[\mathrm{H}_{2(\mathrm{~g})}\right]^{3}}=K_{c}$
$\Rightarrow \frac{x \times 0.02}{0.3 \times(0.1)^{3}}=3.90$
$\Rightarrow x=\frac{3.90 \times 0.3 \times(0.1)^{3}}{0.02}$
$=\frac{0.00117}{0.02}$
$=0.0585 \mathrm{M}$
$=5.85 \times 10^{-2} \mathrm{M}$
Hence, the concentration of $\mathrm{CH}_{4}$ at equilibrium is $5.85 \times 10^{-2} \mathrm{M}$.
Question 35: What is meant by the conjugate acid-base pair? Find the conjugate acid/base for the following species:
$\mathrm{HNO}_{2}, \mathrm{CN}^{-}, \mathrm{HClO}_{4}, \mathrm{~F}^{-}, \mathrm{OH}^{-}, \mathrm{CO}_{3}^{2-}$, and $\mathrm{S}^{-}$
Solution. A conjugate acid-base pair is a pair that differs only by one proton.
The conjugate acid-base for the given species is mentioned in the table below.

Question 36: Which of the followings are Lewis acids? $\mathrm{H}_{2} \mathrm{O}, \mathrm{BF}_{3}, \mathrm{H}^{+}$, and $\mathrm{NH}_{4}^{+}$
Solution. Lewis acids are those acids which can accept a pair of electrons. For example, $\mathrm{BF}_{3}, \mathrm{H}^{+}$, and $\mathrm{NH}_{4}^{+}$ are Lewis acids.
Question 37: What will be the conjugate bases for the Brönsted acids: $\mathrm{HF}_{1} \mathrm{H}_{2} \mathrm{SO}_{4}$ and $\mathrm{HCO}_{3}$ ?
Solution. The table below lists the conjugate bases for the given Bronsted acids.

Question 38: Write the conjugate acids for the following Brönsted bases: $\mathrm{NH}_{2}^{-}, \mathrm{NH}_{3}$ and $\mathrm{HCOO}^{-}$.
Solution. The table below lists the conjugate acids for the given Bronsted bases.

Question $39:$ The species: $\mathrm{H}_{2} \mathrm{O}, \mathrm{HCO}_{3}^{-}, \mathrm{HSO}_{4}^{-}$, and $\mathrm{NH}_{3}$ can act both as Brönsted acids and bases. For each case give the corresponding conjugate acid and base.
Solution. The table below lists the conjugate acids and conjugate bases for the given species.

Question 40: Classify the following species into Lewis acids and Lewis bases and show how these act as Lewis acid/base: (a) $\mathrm{OH}^{-}$ (b) $\mathrm{F}^{-}$ (c) $\mathrm{H}^{+}$ (d) $\mathrm{BCl}_{3}$.
Solution. (a) $\mathrm{OH}^{-}$ is a Lewis base since it can donate its lone pair of electrons.
(b) $\mathrm{F}^{-}$ is a Lewis base since it can donate a pair of electrons.
(c) $\mathrm{H}^{+}$ is a Lewis acid since it can accept a pair of electrons.
(d) $\mathrm{BCl}_{3}$ is a Lewis acid since it can accept a pair of electrons.
Question 41: The concentration of hydrogen ion in a sample of soft drink is $3.8 \times 10^{-3} \mathrm{M}$. what is its $\mathrm{pH}$ ?
Solution. Given,
$\left[\mathrm{H}^{+}\right]=3.8 \times 10^{-3} \mathrm{M}$
$\therefore \mathrm{pH}$ value of soft drink
$=-\log \left[\mathrm{H}^{+}\right]$
$=-\log \left(3.8 \times 10^{-3}\right)$
$=-\log 3.8-\log 10^{-3}$
$=-\log 3.8+3$
$=-0.58+3$
$=2.42$
Question $42$ : The $\mathrm{pH}$ of a sample of vinegar is $3.76 .$ Calculate the concentration of hydrogen ion in it.
Solution. Given,
$\mathrm{pH}=3.76$
It is known that,
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$\Rightarrow \log \left[\mathrm{H}^{+}\right]=-\mathrm{pH}$
$\Rightarrow\left[\mathrm{H}^{+}\right]=\operatorname{antilog}(-\mathrm{pH})$
$=\operatorname{antil} \operatorname{og}(-3.76)$
$=1.74 \times 10^{-4} \mathrm{M}$
Hence, the concentration of hydrogen ion in the given sample of vinegar is $1.74 \times 10^{-4} \mathrm{M}$.
Question $43:$ mThe ionization constant of HF, HCOOH and HCN at $298 \mathrm{~K}$ are
$6.8 \times 10^{-4}, 1.8 \times 10^{-4}$ and $4.8 \times 10^{-9}$ respectively. Calculate the ionization constants of the corresponding conjugate base
Solution. It is known that,
$K_{b}=\frac{K_{w}}{K_{a}}$
Given,
$K_{a}$ of $\mathrm{HF}=6.8 \times 10^{-4}$
Hence, $K_{b}$ of its conjugate base $\mathrm{F}^{-}$
$=\frac{K_{w}}{K_{a}}$
$=\frac{10^{-14}}{6.8 \times 10^{-4}}$
$=1.5 \times 10^{-11}$
Given,
$K_{a}$ of $\mathrm{HCOOH}=1.8 \times 10^{-4}$
Hence, $K_{b}$ of its conjugate base $\mathrm{HCOO}^{-}$
$=\frac{K_{w}}{K_{a}}$
$=\frac{10^{-14}}{1.8 \times 10^{-4}}$
$=5.6 \times 10^{-11}$
Given,
$K_{a}$ of $\mathrm{HCN}=4.8 \times 10^{-9}$
Hence, $K_{b}$ of its conjugate base $\mathrm{CN}^{-}$
$=\frac{K_{w}}{K_{a}}$
$=\frac{10^{-14}}{4.8 \times 10^{-9}}$
$=2.08 \times 10^{-6}$’
Question $44$ : The ionization constant of phenol is $1.0 \times 10^{-10} .$ What is the concentration of phenolate ion in $0.05 \mathrm{M}$ solution of phenol? What will be its degree of ionization if the solution is also $0.01 \mathrm{M}$ in sodium phenolate?
Solution. lonization of phenol:
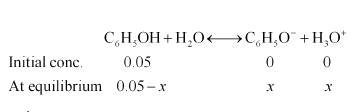
$K_{a}=\frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{OH}\right]}$
$K_{\sigma}=\frac{x \times x}{0.05-x}$
As the value of the tonization constant is very less, $x$ will be very small. Thus,
we can ignore $x$ in the denominator.
$\therefore x=\sqrt{1 \times 10^{-10} \times 0.05}$
$=\sqrt{5 \times 10^{-12}}$
$=2.2 \times 10^{-6} \mathrm{M}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]$
Since $\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]$
Now, let $\propto$ be the degree of ionization of phenol in the presence of $0.01 \mathrm{M} \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{ONa}$.
$\begin{array}{rr} & \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{ONa} \longrightarrow \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}+\mathrm{Na}^{+} \\ \text {Conc. } & 0.01\end{array}$
Also,
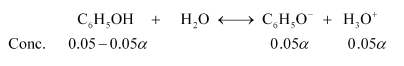
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{OH}\right]=0.05-0.05 \alpha ; 0.05 \mathrm{M}$
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]=0.01+0.05 \alpha ; 0.01 \mathrm{M}$
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=0.05 \alpha$
$K_{a}=\frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{OH}\right]}$
$K_{a}=\frac{(0.01)(0.05 \alpha)}{0.05}$
$1.0 \times 10^{-10}=.01 \alpha$
$\alpha=1 \times 10^{-8}$
Question $45$ : also? If the second dissociation constant of $\mathrm{H}_{2} \mathrm{~S}$ is $1.2 \times 10^{-13}$, calculate the concentration of $\mathrm{S}^{2-}$ under both conditions.
Solution. (i) To calculate the concentration of $\mathrm{HS}^{-}$ ion:
Case I (in the absence of $\mathrm{HCl}$ ):
Let the concentration of $\mathrm{HS}^{-}$ be $\times \mathrm{M}$.
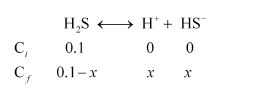
Then, $K_{a_{1}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{HS}^{-}\right]}{\left[\mathrm{H}_{2} \mathrm{~S}\right]}$
$9.1 \times 10^{-8}=\frac{(x)(x)}{0.1-x}$
$\left(9.1 \times 10^{-8}\right)(0.1-x)=x^{2}$
Taking $0.1-x \mathrm{M} ; 0.1 \mathrm{M}$, we have $\left(9.1 \times 10^{-8}\right)(0.1)=x^{2}$.
$9.1 \times 10^{-9}=x^{2}$
$x=\sqrt{9.1 \times 10^{-9}}$
$=9.54 \times 10^{-5} \mathrm{M}$
$=9.54 \times 10^{-5} \mathrm{M}$
$\Rightarrow\left[\mathrm{HS}^{-}\right]=9.54 \times 10^{-5} \mathrm{M}$
Case II (in the presence of $\mathrm{HCl}$ ):
In the presence of $0.1 \mathrm{M}$ of $\mathrm{HCl}$, let $\left[\mathrm{HS}^{-}\right]$ be $y \mathrm{M}$.
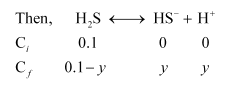

Now, $K_{o_{1}}=\frac{\left[\mathrm{HS}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{H}_{2} \mathrm{~S}\right]}$
$K_{a_{1}}=\frac{[y](0.1+y)}{(0.1-y)}$
$9.1 \times 10^{-8}=\frac{y \times 0.1}{0.1}$
$(\because 0.1-y ; 0.1 \mathrm{M})$
$($ and $0.1+y ; 0.1 \mathrm{M})$
$9.1 \times 10^{-8}=y$
$\Rightarrow\left[\mathrm{HS}^{-}\right]=9.1 \times 10^{-8}$
(ii) To calculate the concentration of $\left[\mathrm{S}^{2-}\right]$
Case I (in the absence of $0.1 \mathrm{M} \mathrm{HCl}$ ):
$\mathrm{HS}^{-} \longleftrightarrow \mathrm{H}^{+}+\mathrm{S}^{2-}$
$\left[\mathrm{HS}^{-}\right]=9.54 \times 10^{-5} \mathrm{M}$ (From first ionization, case I)
Let $\left[\mathrm{S}^{2-}\right]$ be $X$.
Also, $\left[\mathrm{H}^{+}\right]=9.54 \times 10^{-5} \mathrm{M}$ (From first ionization, case I)
$K_{a_{2}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]}$
$K_{a_{2}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]}$
$K_{a_{2}}=\frac{\left(9.54 \times 10^{-5}\right)(X)}{9.54 \times 10^{-5}}$
$1.2 \times 10^{-13}=X=\left[\mathrm{S}^{2-}\right]$
Case II (in the presence of $0.1 \mathrm{M} \mathrm{HCl}$ ):
Again, let the concentration of $\mathrm{HS}^{-}$ be $X^{\prime} \mathrm{M}$.
$\left[\mathrm{HS}^{-}\right]=9.1 \times 10^{-8} \mathrm{M}$ (From first ionization, case II)
$\left[\mathrm{H}^{+}\right]=0.1 \mathrm{M}$ (From $\mathrm{HCl}$, case II $)$
$\left[\mathrm{S}^{2-}\right]=X^{\prime}$
Then, $K_{a_{2}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]}$
$1.2 \times 10^{-13}=\frac{(0.1)\left(X^{\prime}\right)}{9.1 \times 10^{-8}}$
$10.92 \times 10^{-21}=0.1 X^{\prime}$
$\frac{10.92 \times 10^{-21}}{0.1}=X^{\prime}$
$X^{\prime}=\frac{1.092 \times 10^{-20}}{0.1}$
$=1.092 \times 10^{-19} \mathrm{M}$
$\Rightarrow K_{a_{1}}=1.74 \times 10^{-5}$
Question $46$ : The ionization constant of acetic acid is $1.74 \times 10^{-5}$. Calculate the degree of dissociation of acetic acid in its $0.05 \mathrm{M}$ solution. Calculate the concentration of acetate ion in the solution and its $\mathrm{pH}$.
Solution. Method 1
1) $\mathrm{CH}_{3} \mathrm{COOH} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}^{+} \quad K_{a}=1.74 \times 10^{-5}$
2) $\mathrm{H}_{2} \mathrm{O}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{OH}^{-} \quad K_{w}=1.0 \times 10^{-14}$
Since $K a \gg K_{w,}$ :
$\mathrm{CH}_{3} \mathrm{COOH}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}_{3} \mathrm{O}^{+}$

$K_{a}=\frac{(.05 \alpha)(.05 \alpha)}{(.05-0.05 \alpha)}$
$0.05 \alpha^{2}+1.74 \times 10^{-5} \alpha-1.74 \times 10^{-5}$
$D=b^{2}-4 a c$
$=\left(1.74 \times 10^{-5}\right)^{2}-4(.05)\left(1.74 \times 10^{-5}\right)$
$=3.02 \times 10^{-25}+.348 \times 10^{-5}$
$\alpha=\sqrt{\frac{K_{a}}{c}}$
$\alpha=\sqrt{\frac{1.74 \times 10^{-5}}{.05}}$
$=\sqrt{\frac{34.8 \times 10^{-5} \times 10}{10}}$
$=\sqrt{3.48 \times 10^{-6}}$
$=\mathrm{CH}_{3} \mathrm{COOH} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}^{+}$
$\alpha 1.86 \times 10^{-3}$
$\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]=0.05 \times 1.86 \times 10^{-3}$
$=\frac{0.93 \times 10^{-3}}{1000}$
$=.000093$
Method 2
Degree of dissociation,
$\alpha=\sqrt{\frac{K_{a}}{c}}$
$c=0.05 \mathrm{M}$
$K_{a}=1.74 \times 10^{-5}$
Then, $\alpha=\sqrt{\frac{1.74 \times 10^{-5}}{.05}}$
$\alpha=\sqrt{34.8 \times 10^{-5}}$
$\alpha=\sqrt{3.48} \times 10^{-4}$
$\alpha=1.8610^{-2}$
$\mathrm{CH}_{3} \mathrm{COOH} \longleftrightarrow \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}^{+}$
Thus, concentration of $\mathrm{CH}_{3} \mathrm{COO}-=\mathrm{c} . \mathrm{a}$
$=.05 \times 1.86 \times 10^{-2}$
$=.093 \times 10^{-2}$
$=.00093 \mathrm{M}$
Since $\left[\mathrm{oAc}^{-}\right]=\left[\mathrm{H}^{+}\right]$
$\left[\mathrm{H}^{+}\right]=.00093=.093 \times 10^{-2} .$
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$=-\log \left(.093 \times 10^{-2}\right)$
$\therefore \mathrm{pH}=3.03$
Hence, the concentration of acetate ion in the solution is $0.00093 \mathrm{M}$ and its $\mathrm{Ph}$ is $3.03$.
Question 47: It has been found that the $\mathrm{pH}$ of a $0.01 \mathrm{M}$ solution of an organic acid is $4.15 .$ Calculate the concentration of the anion, the ionization constant of the acid and its $\mathrm{pK}_{\mathrm{a}}$
Solution. Let the organic acid be $\mathrm{HA}$.
$\Rightarrow \mathrm{HA} \longleftrightarrow \mathrm{H}^{+}+\mathrm{A}^{-}$
Concentration of $\mathrm{HA}=0.01 \mathrm{M}$
$\mathrm{pH}=4.15$
$-\log \left[\mathrm{H}^{+}\right]=4.15$
$\left[\mathrm{H}^{+}\right]=7.08 \times 10^{-5}$
Now, $K_{a}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}$
$\left[\mathrm{H}^{+}\right]=\left[\mathrm{A}^{-}\right]=7.08 \times 10^{-5}$
$[\mathrm{HA}]=0.01$
Then,
$K_{a}=\frac{\left(7.08 \times 10^{-5}\right)\left(7.08 \times 10^{-5}\right)}{0.01}$
$K_{a}=5.01 \times 10^{-7}$
$K_{o}=5.01 \times 10^{-7}$
$=-\log \left(5.01 \times 10^{-7}\right)$
$p K_{a}=6.3001$
Question 48: Assuming complete dissociation, calculate the $\mathrm{pH}$ of the following solutions:
(a) $0.003 \mathrm{M} \mathrm{HCl}$
(b) $0.005 \mathrm{M} \mathrm{NaOH}$
(c) $0.002 \mathrm{M} \mathrm{HBr}$
(d) $0.002 \mathrm{M} \mathrm{KOH}$
Solution. (i) $0.003 \mathrm{MHCl}$ :
$\mathrm{H}_{2} \mathrm{O}+\mathrm{HCl} \longleftrightarrow \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{Cl}^{-}$
Since $\mathrm{HCl}$ is completely ionized,
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{HCl}]$
$\Rightarrow\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=0.003$
Now,
$\mathrm{pH}=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=-\log (.003)$
$=2.52$
Hence, the $\mathrm{pH}$ of the solution is $2.52 .$
(ii) $0.005 \mathrm{MNaOH}$ :
$\mathrm{NaOH}_{(a q)} \longleftrightarrow \mathrm{Na}_{(a q)}^{+}+\mathrm{HO}_{(a q)}^{-}$
$\left[\mathrm{HO}^{-}\right]=[\mathrm{NaOH}]$
$\Rightarrow\left[\mathrm{HO}^{-}\right]=.005$
$\mathrm{pOH}=-\log \left[\mathrm{HO}^{-}\right]=-\log (.005)$
$\mathrm{pOH}=2.30$
$\therefore \mathrm{pH}=14-2.30$
$=11.70$
Hence, the $\mathrm{pH}$ of the solution is $11.70 .$
(iii) $0.002 \mathrm{HBr}$ :
$\mathrm{HBr}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{Br}^{-}$
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{HBr}]$
$\Rightarrow\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=.002$
$\therefore \mathrm{pH}=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]$
$=-\log (0.002)$
$=2.69$
Hence, the $\mathrm{pH}$ of the solution is $2.69$.
(iv) $0.002 \mathrm{M} \mathrm{KOH}$ :
$\mathrm{KOH}_{(a q)} \longleftrightarrow \mathrm{K}_{(a q)}^{+}+\mathrm{OH}_{(a q)}^{-}$
$\left[\mathrm{OH}^{-}\right]=[\mathrm{KOH}]$
$\Rightarrow\left[\mathrm{OH}^{-}\right]=.002$
Now, $\mathrm{pOH}=-\log \left[\mathrm{OH}^{-}\right]$
$=2.69$
$\therefore \mathrm{pH}=14-2.69$
$=11.31$
Hence, the $\mathrm{pH}$ of the solution is $11.31$.
Question $49$ : Calculate the $\mathrm{pH}$ of the following solutions:
a) $2 \mathrm{~g}$ of TIOH dissolved in water to give 2 litre of solution.
b) $0.3 \mathrm{~g}$ of $\mathrm{Ca}(\mathrm{OH})_{2}$ dissolved in water to give $500 \mathrm{~mL}$ of solution.
c) $0.3 \mathrm{~g}$ of $\mathrm{NaOH}$ dissolved in water to give $200 \mathrm{~mL}$ of solution.
d) $1 \mathrm{~mL}$ of $13.6 \mathrm{M} \mathrm{HCl}$ is diluted with water to give 1 litre of solution.
Solution. (a) For $2 \mathrm{~g}$ of TIOH dissolved in water to give $2 \mathrm{~L}$ of solution:
$\left[\mathrm{TlOH}_{(a q)}\right]=\frac{2}{2} \mathrm{~g} / \mathrm{L}$
$=\frac{2}{2} \times \frac{1}{221} \mathrm{M}$
$=\frac{1}{221} \mathrm{M}$
$\mathrm{TlOH}_{(a q)} \longrightarrow \mathrm{Tl}_{(a q)}^{+}+\mathrm{OH}_{(a q)}^{-}$
$\left[\mathrm{OH}_{\left(\alpha_{4}\right)}^{-}\right]=\left[\mathrm{TlOH}_{(\alpha q)}\right]=\frac{1}{221} \mathrm{M}$
$K_{w}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]$
$10^{-14}=\left[\mathrm{H}^{+}\right]\left(\frac{1}{221}\right)$
$221 \times 10^{-14}=\left[\mathrm{H}^{+}\right]$
$\Rightarrow \mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]=-\log \left(221 \times 10^{-14}\right)$
$=-\log \left(2.21 \times 10^{-12}\right)$
$=11.65$
(b) For $0.3 \mathrm{~g}$ of $\mathrm{Ca}(\mathrm{OH})_{2}$ dissolved in water to give $500 \mathrm{~mL}$ of solution:
$\mathrm{Ca}(\mathrm{OH})_{2} \longrightarrow \mathrm{Ca}^{2+}+2 \mathrm{OH}^{-}$
$\left[\mathrm{Ca}(\mathrm{OH})_{2}\right]=0.3 \times \frac{1000}{500}=0.6 \mathrm{M}$
$\left[\mathrm{OH}^{-}_{a q}\right]=2 \times\left[\mathrm{Ca}(\mathrm{OH})_{2 \omega q}\right]=2 \times 0.6$
$=1.2 \mathrm{M}$
$\left[\mathrm{H}^{+}\right]=\frac{K_{w}}{\left[\mathrm{OH}^{-}{ }_{a q}\right]}$
$=\frac{10-14}{1.2} \mathrm{M}$
$=0.833 \times 10^{-14}$
$\mathrm{pH}=-\log \left(0.833 \times 10^{-14}\right)$
$=-\log \left(8.33 \times 10^{-13}\right)$
$=(-0.902+13)$
$=12.098$
(c) For $0.3 \mathrm{~g}$ of $\mathrm{NaOH}$ dissolved in water to give $200 \mathrm{~mL}$ of solution:
$\mathrm{NaOH} \longrightarrow \mathrm{Na}_{\left(a_{q)}\right.}^{+}+\mathrm{OH}_{(a q)}^{-}$
$[\mathrm{NaOH}]=0.3 \times \frac{1000}{200}=1.5 \mathrm{M}$
$\left[\mathrm{OH}^{-}{ }_{\omega q}\right]=1.5 \mathrm{M}$
$\left[\mathrm{OH}^{-}{ }_{\omega q}\right]=1.5 \mathrm{M}$
$=6.66 \times 10^{-13}$
$\mathrm{pH}=-\log \left(6.66 \times 10^{-13}\right)$
$=12.18$
(d) For $1 \mathrm{~mL}$ of $13.6 \mathrm{M} \mathrm{HCl}$ diluted with water to give $1 \mathrm{~L}$ of solution:
$13.6 \times 1 \mathrm{~mL}=\mathrm{M}_{2} \times 1000 \mathrm{~mL}$
(Before dilution) (After dilution)
$13.6 \times 10^{-3}=\mathrm{M}_{2} \times 1 \mathrm{~L}$
$\mathrm{M}_{2}=1.36 \times 10^{-2}$
$\left[\mathrm{H}^{+}\right]=1.36 \times 10^{-2}$
$\mathrm{pH}=-\log \left(1.36 \times 10^{-2}\right)$
$=(-0.1335+2)$
$=1.866 \sim 1.87$
Question $50$ The degree of ionization of a $0.1 \mathrm{M}$ bromoacetic acid solution is $0.132 .$ Calculate the $\mathrm{pH}$ of the solution and the $p K_{\mathrm{a}}$ of bromoacetic acid.
Solution. Degree of ionization, $\alpha=0.132$
Concentration, $c=0.1 \mathrm{M}$
Thus, the concentration of $\mathrm{H}_{3} \mathrm{O}^{+}=\mathrm{c.} \alpha$
$=0.1 \times 0.132$
$=0.0132$
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$=-\log (0.0132)$
$=1.879: 1.88$
Now,
$K_{o}=C \alpha^{2}$
$=0.1 \times(0.132)^{2}$
$K_{a}=.0017$
$p K_{a}=2.75$
Question 51: The $\mathrm{pH}$ of $0.005 \mathrm{M}$ codeine $\left(\mathrm{C}_{18} \mathrm{H}_{21} \mathrm{NO}_{3}\right)$ solution is $9.95 .$ Calculate its ionization constant and $\mathrm{pK}_{\mathrm{b}}$.
Solution. $c=0.005$
$\mathrm{pH}=9.95$
$\mathrm{pOH}=4.05$
$\mathrm{pH}=-\log (4.105)$
$4.05=-\log \left[\mathrm{OH}^{-}\right]$
$\left[\mathrm{OH}^{-}\right]=8.91 \times 10^{-5}$
$c \alpha=8.91 \times 10^{-5}$
$\alpha=\frac{8.91 \times 10^{-5}}{5 \times 10^{-3}}=1.782 \times 10^{-2}$
Thus, $K_{h}=c \alpha^{2}$
$=0.005 \times(1.782)^{2} \times 10^{-4}$
$=0.005 \times 3.1755 \times 10^{-4}$
$=0.0158 \times 10^{-4}$
$K_{b}=1.58 \times 10^{-6}$
$P k_{b}=-\log K_{b}$
$=-\log \left(1.58 \times 10^{-6}\right)$
$=5.80$
Question 52: What is the $\mathrm{pH}$ of $0.001 \mathrm{M}$ aniline solution? The ionization constant of aniline can be taken from Table 7.7. Calculate the degree of ionization of aniline in the solution. Also calculate the ionization constant of the conjugate acid of aniline.
Solution. $K_{b}=4.27 \times 10^{-10}$
$c=0.001 \mathrm{M}$
$\mathrm{pH}=?$
$\alpha=?$
$k_{b}=c \alpha^{2}$
$4.27 \times 10^{-10}=0.001 \times \alpha^{2}$
$4270 \times 10^{-10}=\alpha^{2}$
$65.34 \times 10^{-5}=\alpha=6.53 \times 10^{-4}$
Then, $[$ anion $]=c \alpha=.001 \times 65.34 \times 10^{-5}$
$=.065 \times 10^{-5}$
$\mathrm{pOH}=-\log \left(.065 \times 10^{-5}\right)$
$=6.187$
$\mathrm{pH}=7.813$
Now,
$K_{a} \times K_{b}=K_{w}$
$\therefore 4.27 \times 10^{-10} \times K_{a}=K_{w}$
$K_{a}=\frac{10^{-14}}{4.27 \times 10^{-10}}$
$=2.34 \times 10^{-5}$
Thus, the ionization constant of the conjugate acid of aniline is $2.34 \times 10^{-5}$.
Question 53: Calculate the degree of ionization of $0.05 \mathrm{M}$ acetic acid if its $\mathrm{pK}_{\mathrm{a}}$ value is $4.74 .$
Solution. $c=0.05 \mathrm{M}$
$p K_{a}=4.74$
$p K_{a}=-\log \left(K_{o}\right)$
$K_{a}=1.82 \times 10^{-5}$
$K_{a}=c \alpha^{2} \quad \alpha=\sqrt{\frac{K_{a}}{c}}$
$\alpha=\sqrt{\frac{1.82 \times 10^{-5}}{5 \times 10^{-2}}}=1.908 \times 10^{-2}$
When HCl is added to the solution, the concentration of $\mathrm{H}^{+}$ ions will increase. Therefore, the equilibrium will shift in the backward direction i.e., dissociation of acetic acid will decrease.
Case I: When $0.01 \mathrm{M} \mathrm{HCl}$ is taken.
Let $x$ be the amount of acetic acid dissociated after the addition of $\mathrm{HCl}$.
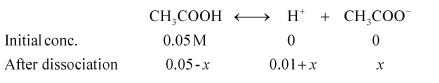
As the dissociation of a very small amount of acetic acid will take place, the values i.e., $0.05-x$ and $0.01+x$ can be taken as $0.05$ and $0.01$ respectively.
$K_{a}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}$
$\therefore K_{a}=\frac{(0.01) x}{0.05}$
$x=\frac{1.82 \times 10^{-5} \times 0.05}{0.01}$
$x=1.82 \times 10^{-3} \times 0.05 \mathrm{M}$
Now,
$\alpha=\frac{\text { Amount of acid dissociated }}{\text { Amount of acid taken }}$
$=\frac{1.82 \times 10^{-3} \times 0.05}{0.05}$
$=1.82 \times 10^{-3}$
Case II: When $0.1 \mathrm{M} \mathrm{HCl}$ is taken.
Let the amount of acetic acid dissociated in this case be $X$. As we have done in the first case, the concentrations of various species involved in the reaction are:
$\left[\mathrm{CH}_{3} \mathrm{COOH}\right]=0.05-X ; 0.05 \mathrm{M}$
$\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]=X$
$\left[\mathrm{H}^{+}\right]=0.1+X ; 0.1 \mathrm{M}$
$K_{a}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}$
$\therefore K_{o}=\frac{(0.1) X}{0.05}$
$x=\frac{1.82 \times 10^{-5} \times 0.05}{0.1}$
$x=1.82 \times 10^{-4} \times 0.05 \mathrm{M}$
Now,
$\alpha=\frac{\text { Amount of acid dissociated }}{\text { Amount of acid taken }}$
$=\frac{1.82 \times 10^{-4} \times 0.05}{0.05}$
$=1.82 \times 10^{-4}$
Question 54: The ionization constant of dimethylamine is $5.4 \times 10^{-4} .$ Calculate its degree of ionization in its $0.02 \mathrm{M}$ solution. What percentage of dimethylamine is ionized if the solution is also $0.1 \mathrm{M}$ in $\mathrm{NaOH} ?$
Solution. $K_{b}=5.4 \times 10^{-4}$
$c=0.02 \mathrm{M}$
Then, $\alpha=\sqrt{\frac{K_{b}}{c}}$
$=\sqrt{\frac{5.4 \times 10^{-4}}{0.02}}$
$=0.1643$
Now, if $0.1 \mathrm{M}$ of $\mathrm{NaOH}$ is added to the solution, then $\mathrm{NaOH}$ (being a strong base) undergoes complete ionization.
$\mathrm{NaOH}_{(a q)} \longleftrightarrow \mathrm{Na}_{(\text {ag) }}^{+}+\mathrm{OH}^{-}_{(a q)}$
$0.1 \mathrm{M} \quad 0.1 \mathrm{M}$
And,
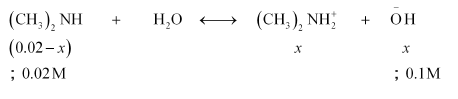
Then, $\left[\left(\mathrm{CH}_{3}\right)_{2} \mathrm{NH}_{2}^{+}\right]=x$
$\left[\mathrm{OH}^{-}\right]=x+0.1 ; 0.1$
$\Rightarrow K_{b}=\frac{\left[\left(\mathrm{CH}_{3}\right)_{2} \mathrm{NH}_{2}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\left(\mathrm{CH}_{3}\right)_{2} \mathrm{NH}\right]}$
$5.4 \times 10^{-4}=\frac{x \times 0.1}{0.02}$
$x=0.0054$
It means that in the presence of $0.1 \mathrm{M} \mathrm{NaOH}, 0.54 \%$ of dimethylamine will get dissociated.
Question $55$ : Calculate the hydrogen ion concentration in the following biological fluids whose $\mathrm{pH}$ are given below:
(a) Human muscle-fluid, $6.83$
(b) Human stomach fluid, $1.2$
(c) Human blood, $7.38$
(d) Human saliva, $6.4$.
Solution. (a) Human muscle fluid 6.83:
$\mathrm{pH}=6.83$
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$\therefore 6.83=-\log \left[\mathrm{H}^{+}\right]$
$\left[\mathrm{H}^{+}\right]=1.48 \times 10^{-7} \mathrm{M}$
(b) Human stomach fluid, 1.2:
$\mathrm{pH}=1.2$
$1.2=-\log \left[\mathrm{H}^{+}\right]$
$\therefore\left[\mathrm{H}^{+}\right]=0.063$
(c) Human blood, $7.38$ :
$\mathrm{pH}=7.38=-\log \left[\mathrm{H}^{+}\right]$
$\therefore\left[\mathrm{H}^{+}\right]=4.17 \times 10^{-8} \mathrm{M}$
(d) Human saliva, $6.4$ :
$\mathrm{pH}=6.4$
$6.4=-\log \left[\mathrm{H}^{+}\right]$
$\left[\mathrm{H}^{+}\right]=3.98 \times 10^{-7}$
Question $56$ : The $\mathrm{pH}$ of milk, black coffee, tomato juice, lemon juice and egg white are $6.8,5.0,4.2,2.2$ and $7.8$ respectively. Calculate corresponding hydrogen ion concentration in each.
Solution. The hydrogen ion concentration in the given substances can be calculated by using the given relation:
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
(i) $\mathrm{pH}$ of milk $=6.8$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$6.8=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-6.8$
$\left[\mathrm{H}^{+}\right]=\operatorname{anitlog}(-6.8)$
$=1.5 \times 10^{-7} \mathrm{M}$
(ii) $\mathrm{pH}$ of black coffee $=5.0$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$5.0=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-5.0$
$\left[\mathrm{H}^{+}\right]=$ anitlog $(-5.0)$
$=10^{-5} \mathrm{M}$
(iii) $\mathrm{pH}$ of tomato juice $=4.2$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$4.2=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-4.2$
$\left[\mathrm{H}^{+}\right]=\operatorname{anitlog}(-4.2)$
$=6.31 \times 10^{-5} \mathrm{M}$
(iv) $\mathrm{pH}$ of lemon juice $=2.2$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$2.2=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-2.2$
$\left[\mathrm{H}^{+}\right]=\operatorname{anitlog}(-2.2)$
$=6.31 \times 10^{-3} \mathrm{M}$
(v) $\mathrm{pH}$ of egg white $=7.8$
Since, $\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$7.8=-\log \left[\mathrm{H}^{+}\right]$
$\log \left[\mathrm{H}^{+}\right]=-7.8$
$\left[\mathrm{H}^{+}\right]=\operatorname{anitlog}(-7.8)$
$=1.58 \times 10^{-8} \mathrm{M}$
Question $57:$ If $0.561 \mathrm{~g}$ of $\mathrm{KOH}$ is dissolved in water to give $200 \mathrm{~mL}$ of solution at $298 \mathrm{~K}$. Calculate the concentrations of potassium, hydrogen and hydroxyl ions. What is its $\mathrm{pH}$ ?
Solution. $\left[\mathrm{KOH}_{a q}\right]=\frac{0.561}{\frac{1}{5}} \mathrm{~g} / L$
$=2.805 \mathrm{~g} / L$
$=2.805 \times \frac{1}{56.11} \mathrm{M}$
$=.05 \mathrm{M}$
$\mathrm{KOH}_{(a q)} \rightarrow \mathrm{K}_{(a q)}^{+}+\mathrm{OH}_{(a q)}^{-}$
$\left[\mathrm{OH}^{-}\right]=.05 \mathrm{M}=\left[\mathrm{K}^{+}\right]$
$\left[\mathrm{H}^{+}\right]\left[\mathrm{H}^{-}\right]=K_{\mathrm{w}}$
$\left[\mathrm{H}^{+}\right] \frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}$
$=\frac{10^{-14}}{0.05}=2 \times 10^{-13} \mathrm{M}$
$=\frac{10^{-14}}{0.05}=2 \times 10^{-13} \mathrm{M}$
$\therefore \mathrm{pH}=12.70$
Question $58:$ The solubility of $\mathrm{Sr}(\mathrm{OH})_{2}$ at $298 \mathrm{~K}$ is $19.23 \mathrm{~g} / \mathrm{L}$ of solution. Calculate the concentrations of strontium and hydroxyl ions and the $\mathrm{pH}$ of the solution.
Solution. Solubility of $\mathrm{Sr}(\mathrm{OH})_{2}=19.23 \mathrm{~g} / \mathrm{L}$
Then, concentration of $\mathrm{Sr}(\mathrm{OH})_{2}$
$=\frac{19.23}{121.63} \mathrm{M}$
$=0.1581 \mathrm{M}$
$\mathrm{Sr}(\mathrm{OH})_{2(a q)} \longrightarrow \mathrm{Sr}^{2+}{ }_{(\mathrm{aq})}+2\left(\mathrm{OH}^{-}\right)_{(a q)}$
$\therefore\left[\mathrm{Sr}^{2+}\right]=0.1581 \mathrm{M}$
$\left[\mathrm{OH}^{-}\right]=2 \times 0.1581 \mathrm{M}=0.3126 \mathrm{M}$
Now,
$K_{w}=\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}^{+}\right]$
$\frac{10^{-14}}{0.3126}=\left[\mathrm{H}^{+}\right]$
$\Rightarrow\left[\mathrm{H}^{+}\right]=3.2 \times 10^{-14}$
$\therefore \mathrm{pH}=13.495 ; 13.50$
Question 59: The ionization constant of propanoic acid is $1.32 \times 10^{-5} .$ Calculate the degree of ionization of the acid in its $0.05 \mathrm{M}$ solution and also its $\mathrm{pH}$. What will be its degree of ionization if the solution is $0.01 \mathrm{M}$ in $\mathrm{HCl}$ also?
Solution. Let the degree of ionization of propanoic acid be $\alpha$.
Then, representing propionic acid as HA, we have:
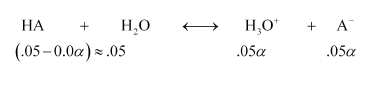
$K_{a}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}$
$=\frac{(.05 \alpha)(.05 \alpha)}{0.05}=.05 \alpha^{2}$
$\alpha=\sqrt{\frac{K_{a}}{.05}}=1.63 \times 10^{-2}$
Then, $\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=.05 \alpha=.05 \times 1.63 \times 10^{-2}=K_{b} .15 \times 10^{-4} \mathrm{M}$
$\therefore \mathrm{pH}=3.09$
In the presence of $0.1 \mathrm{M}$ of $\mathrm{HCl}$, let $\alpha$ ' be the degree of ionization.
Then, $\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=0.01$
$\left[\mathrm{A}^{-}\right]=005 \alpha^{\prime}$
$[\mathrm{HA}]=.05$
$K_{a}=\frac{0.01 \times .05 \alpha^{\prime}}{.05}$
$1.32 \times 10^{-5}=.01 \times \alpha^{\prime}$
$\alpha^{\prime}=1.32 \times 10^{-3}$
Question $60:$ The $\mathrm{pH}$ of $0.1 \mathrm{M}$ solution of cyanic acid (HCNO) is 2.34. Calculate the ionization constant of the acid and its degree of ionization in the solution.
Solution. $c=0.1 \mathrm{M}$
$\mathrm{pH}=2.34$
$-\log \left[\mathrm{H}^{+}\right]=\mathrm{pH}$
$-\log \left[\mathrm{H}^{+}\right]=2.34$
$\left[\mathrm{H}^{+}\right]=4.5 \times 10^{-3}$
Also,
$\left[\mathrm{H}^{+}\right]=c \alpha$
$4.5 \times 10^{-3}=0.1 \times \alpha$
$\frac{4.5 \times 10^{-3}}{0.1}=\alpha$
$\alpha=45 \times 10^{-3}=.045$
Then,
$K_{a}=c \alpha^{2}$
$=0.1 \times\left(45 \times 10^{-3}\right)^{2}$
$=202.5 \times 10^{-6}$
$=2.02 \times 10^{-4}$
Question 61: The ionization constant of nitrous acid is $4.5 \times 10^{-4} .$ Calculate the pH of $0.04 \mathrm{M}$ sodium nitrite solution and also its degree of hydrolysis.
Solution. $\mathrm{NaNO}_{2}$ is the salt of a strong base ( $\mathrm{NaOH}$ ) and a weak acid $\left(\mathrm{HNO}_{2}\right) .$
$\mathrm{NO}_{2}^{-}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{HNO}_{2}+\mathrm{OH}^{-}$
$K_{h}=\frac{\left[\mathrm{HNO}_{2}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NO}_{2}^{-}\right]}$
$\Rightarrow \frac{K_{w}}{K_{a}}=\frac{10^{-14}}{4.5 \times 10^{-4}}=.22 \times 10^{-10}$
Now, If $x$ moles of the salt undergo hydrolysis, then the concentration of various species present in the solution will be
$\left[\mathrm{NO}_{2}^{-}\right]=.04-x ; 0.04$
$\left[\mathrm{HNO}_{2}\right]=x$
$\left[\mathrm{OH}^{-}\right]=x$
$K_{h}=\frac{x^{2}}{0.04}=0.22 \times 10^{-10}$
$x^{2}=.0088 \times 10^{-10}$
$x=.093 \times 10^{-5}$
$\therefore\left[\mathrm{OH}^{-}\right]=0.093 \times 10^{-5} \mathrm{M}$
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{10^{-14}}{.093 \times 10^{-5}}=10.75 \times 10^{-9} \mathrm{M}$
$\Rightarrow \mathrm{pH}=-\log \left(10.75 \times 10^{-9}\right)$
$=7.96$
Therefore, degree of hydrolysis
$=\frac{x}{0.04}=\frac{.093 \times 10^{-5}}{.04}=2.325 \times 10^{-5}$
Question $62$ : A $0.02 \mathrm{M}$ solution of pyridinium hydrochloride has $\mathrm{pH}=3.44$. Calculate the ionization constant of pyridine
Solution. $\mathrm{pH}=3.44$
We know that,
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$\therefore\left[\mathrm{H}^{+}\right]=3.63 \times 10^{-4}$
Then, $K_{h}=\frac{\left(3.63 \times 10^{-4}\right)^{2}}{0.02}$
$(\because$ concentration $=0.02 \mathrm{M})$
$\Rightarrow K_{h}=6.6 \times 10^{-6}$
$\mathrm{Now}, K_{h}=\frac{K_{w}}{K_{a}}$
$\Rightarrow K_{a}=\frac{K_{w}}{K_{h}}=\frac{10^{-14}}{6.6 \times 10^{-6}}$
$=1.51 \times 10^{-9}$
Question 63: Predict if the solutions of the following salts are neutral, acidic or basic:
$\mathrm{NaCl}, \mathrm{KBr}, \mathrm{NaCN}, \mathrm{NH}_{4} \mathrm{NO}_{3}, \mathrm{NaNO}_{2}$ and $\mathrm{KF}$
Solution. (i) $\mathrm{NaCl}$ :
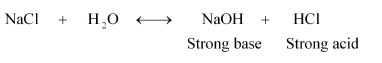
Therefore, it is a neutral solution.
(ii) KBr:

Therefore, it is a neutral solution.
(iii) NaCN:

Therefore, it is a basic solution.
(iv) $\mathrm{NH}_{4} \mathrm{NO}_{3}$

Therefore, it is an acidic solution.
(v) $\mathrm{NaNO}_{2}$
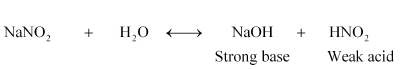
Therefore, it is a basic solution.
(vi) $\mathrm{KF}$
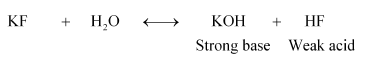
Therefore, it is a basic solution.
Question 64: The ionization constant of chloroacetic acid is $1.35 \times 10^{-3}$. What will be the $\mathrm{pH}$ of $0.1 \mathrm{M}$ acid and its $0.1 \mathrm{M}$ sodium salt solution?
Solution. It is given that $K_{a}$ for $\mathrm{ClCH}_{2} \mathrm{COOH}$ is $1.35 \times 10^{-3}$.
$\Rightarrow K_{a}=c \alpha^{2}$
$\therefore \alpha=\sqrt{\frac{K_{a}}{c}}$
$=\sqrt{\frac{1.35 \times 10^{-3}}{0.1}}$
$(\therefore$ concentration of acid $=0.1 \mathrm{~m})$
$\alpha=\sqrt{1.35 \times 10^{-2}}$
$=0.116$
$\therefore\left[\mathrm{H}^{+}\right]=c \alpha=0.1 \times 0.116$
$=.0116$
$\Rightarrow \mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]=1.94$
$\mathrm{CICH}_{2} \mathrm{COONa}$ is the salt of a weak acid i.e., $\mathrm{ClCH}_{2} \mathrm{COOH}$ and a strong base i.e., $\mathrm{NaOH}$.
$\mathrm{ClCH}_{2} \mathrm{COO}^{-}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{ClCH}_{2} \mathrm{COOH}+\mathrm{OH}^{-}$
$K_{h}=\frac{\left[\mathrm{ClCH}_{2} \mathrm{COOH}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{ClCH}_{2} \mathrm{COO}^{-}\right]}$
$K_{h}=\frac{K_{w}}{K_{a}}$
$K_{h}=\frac{10^{-14}}{1.35 \times 10^{-3}}$
$=0.740 \times 10^{-11}$
Also, $K_{h}=\frac{x^{2}}{0.1}$
(where $x$ is the concentration of $\mathrm{OH}^{-}$ and $\left.\mathrm{ClCH}_{2} \mathrm{COOH}\right)$
$0.740 \times 10^{-11}=\frac{x^{2}}{0.1}$
$0.074 \times 10^{-11}=x^{2}$
$\Rightarrow x^{2}=0.74 \times 10^{-12}$
$x=0.86 \times 10^{-6}$
$\left[\mathrm{OH}^{-}\right]=0.86 \times 10^{-6}$
$\therefore\left[\mathrm{H}^{+}\right]=\frac{K_{w}}{0.86 \times 10^{-6}}$
$=\frac{10^{-14}}{0.86 \times 10^{-6}}$
$\left[\mathrm{H}^{+}\right]=1.162 \times 10^{-8}$
$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$=7.94$
Question $65$ :lonic product of water at $310 \mathrm{~K}$ is $2.7 \times 10^{-14}$. What is the pH of neutral water at this temperature?
Solution. lonic product,
$K_{w}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]$
$\operatorname{Let}\left[\mathrm{H}^{+}\right]=x$
Since $\left[\mathrm{H}^{+}\right]=\left[\mathrm{OH}^{-}\right], K_{\mathrm{w}}=x^{2}$
$\Rightarrow K_{\mathrm{w}}$ at $310 \mathrm{~K}$ is $2.7 \times 10^{-14}$
$\therefore 2.7 \times 10^{-14}=x^{2}$
$\Rightarrow x=1.64 \times 10^{-7}$
$\Rightarrow\left[\mathrm{H}^{+}\right]=1.64 \times 10^{-7}$
$\Rightarrow \mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]$
$=-\log \left[1.64 \times 10^{-7}\right]$
$=6.78$
Question 66: Calculate the $\mathrm{pH}$ of the resultant mixtures:
a) $10 \mathrm{~mL}$ of $0.2 \mathrm{M} \mathrm{Ca}(\mathrm{OH})_{2}+25 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{HCl}$
b) $10 \mathrm{~mL}$ of $0.01 \mathrm{M} \mathrm{H}_{2} \mathrm{SO}_{4}+10 \mathrm{~mL}$ of $0.01 \mathrm{M} \mathrm{Ca}(\mathrm{OH})_{2}$
c) $10 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{H}_{2} \mathrm{SO}_{4}+10 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{KOH}$
Solution. (a) Moles of $\mathrm{H}_{3} \mathrm{O}^{+}=\frac{25 \times 0.1}{1000}=.0025 \mathrm{~mol}$
Moles of $\mathrm{OH}^{-}=\frac{10 \times 0.2 \times 2}{1000}=.0040 \mathrm{~mol}$
Thus, excess of $\mathrm{OH}^{-}=.0015 \mathrm{~mol}$
$\left[\mathrm{OH}^{-}\right]=\frac{.0015}{35 \times 10^{-3}} \mathrm{~mol} / \mathrm{L}=.0428$
$\mathrm{pOH}=-\log [\mathrm{OH}]$
$=1.36$
$\mathrm{pH}=14-1.36$
$=12.63 \quad$ (not matched)
(b) Moles of $\mathrm{H}_{3} \mathrm{O}^{+}=\frac{2 \times 10 \times 0.01}{1000}=.0002
\mathrm{~mol}$
Moles of $\mathrm{OH}^{-}=\frac{2 \times 10 \times .01}{1000}=.0002 \mathrm{~mol}$
Since there is neither an excess of $\mathrm{H}_{3} \mathrm{O}^{+}$ or $\mathrm{OH}^{-}$, the solution is neutral. Hence, $\mathrm{pH}=7$.
(c) Moles of $\mathrm{H}_{3} \mathrm{O}^{+}=\frac{2 \times 10 \times 0.1}{1000}=.002 \mathrm{~mol}$
Moles of $\mathrm{OH}^{-}=\frac{10 \times 0.1}{1000}=0.001 \mathrm{~mol}$
Excess of $\mathrm{H}_{3} \mathrm{O}^{+}=.001 \mathrm{~mol}$
Thus, $\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{.001}{20 \times 10^{-3}}$
$=\frac{10^{-3}}{20 \times 10^{-3}}=.05$
$\therefore \mathrm{pH}=-\log (0.05)$
$=1.30$
Question 67: Determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at $298 \mathrm{~K}$ from their solubility product constants given in Table $7.9$ (page 221). Determine also the molarities of individual ions.
Solution. (1) Silver chromate:
$\mathrm{Ag}_{2} \mathrm{CrO}_{4} \longrightarrow 2 \mathrm{Ag}^{+}+\mathrm{CrO}_{4}^{2-}$
Then,
$K_{s p}=\left[\mathrm{Ag}^{+}\right]^{2}\left[\mathrm{CrO}_{4}{ }^{2-}\right]$
$\Rightarrow 1.1 \times 10^{-12}=4 s^{3}$
$.275 \times 10^{-12}=s^{3}$
$s=0.65 \times 10^{-4} \mathrm{M}$
Molarity of $\mathrm{Ag}^{+}=2 \mathrm{~s}=2 \times 0.65 \times 10^{-4}$
$=1.30 \times 10^{-4} \mathrm{M}$
Molarity of $\mathrm{CrO}_{4}{ }^{2-}=s=0.65 \times 10^{-4} \mathrm{M}$
(2) Barium chromate:
$\mathrm{BaCrO}_{4} \longrightarrow \mathrm{Ba}^{2+}+\mathrm{CrO}_{4}^{2-}$
Then, $K_{s p}=\left[\mathrm{Ba}^{2+}\right]\left[\mathrm{CrO}_{4}^{2-}\right]$
Let $s$ be the solubility of $\mathrm{BaCrO}_{4}$.
Thus, $\left[\mathrm{Ba}^{2+}\right]=\mathrm{s}$ and $\left[\mathrm{CrO}_{4}{ }^{2-}\right]=\mathrm{s}$
$\Rightarrow K_{S P}=s^{2}$
$\Rightarrow 1.2 \times 10^{-10}=s^{2}$
$\Rightarrow s=1.09 \times 10^{-5} \mathrm{M}$
Molarity of $\mathrm{Ba}^{2+}=$ Molarity of $\mathrm{CrO}_{4}{ }^{2-}=s=1.09 \times 10^{-5} \mathrm{M}$
(3) Ferric hydroxide:
$\mathrm{Fe}(\mathrm{OH})_{3} \longrightarrow \mathrm{Fe}^{2+}+3 \mathrm{OH}^{-}$
$K_{s p}=\left[\mathrm{Fe}^{2+}\right]\left[\mathrm{OH}^{-}\right]^{3}$
Let $s$ be the solubility of $\mathrm{Fe}(\mathrm{OH})_{3}$.
Thus, $\left[\mathrm{Fe}^{3+}\right]=s$ and $\left[\mathrm{OH}^{-}\right]=3 s$
$\Rightarrow K_{s p}=s .(3 s)^{3}$
$=s .27 s^{3}$
$K_{s p}=27 s^{4}$
$1.0 \times 10^{-38}=27 s^{4}$
$.037 \times 10^{-38}=s^{4}$
$.00037 \times 10^{-36}=s^{4} \quad \Rightarrow 1.39 \times 10^{-10} \mathrm{M}=\mathrm{S}$
Molarity of $\mathrm{Fe}^{3+}=s=1.39 \times 10^{-10} \mathrm{M}$
Molarity of $\mathrm{OH}^{-}=3 s=4.17 \times 10^{-10} \mathrm{M}$
(4) Lead chloride:
$\mathrm{PbCl}_{2} \longrightarrow \mathrm{Pb}^{2+}+2 \mathrm{Cl}^{-}$
$K_{S P}=\left[\mathrm{Pb}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}$
Let $K_{S P}$ be the solubility of $\mathrm{PbCl}_{2}$.
$\left[\mathrm{PB}^{2+}\right]=s$ and $\left[\mathrm{Cl}^{-}\right]=2 s$
Thus, $K_{s p}=s .(2 s)^{2}$
$=4 s^{3}$
$\Rightarrow 1.6 \times 10^{-5}=4 s^{3}$
$\Rightarrow 0.4 \times 10^{-5}=s^{3}$
$4 \times 10^{-6}=s^{3} \Rightarrow 1.58 \times 10^{-2} \mathrm{M}=\mathrm{S} .1$
Molarity of $\mathrm{PB}^{2+}=s=1.58 \times 10^{-2} \mathrm{M}$
Molarity of chloride $=2 s=3.16 \times 10^{-2} \mathrm{M}$
(5) Mercurous iodide:
$\mathrm{Hg}_{2} \mathrm{I}_{2} \longrightarrow \mathrm{Hg}^{2+}+2 \mathrm{I}^{-}$
$K_{s p}=\left[\mathrm{Hg}_{2}^{2+}\right]^{2}\left[\mathrm{I}^{-}\right]^{2}$
Let $\mathrm{s}$ be the solubility of $\mathrm{Hg}_{2} \mathrm{I}_{2}$.
$\Rightarrow\left[\mathrm{Hg}_{2}^{2+}\right]=s$ and $\left[\mathrm{I}^{-}\right]=2 s$
Thus, $K_{x p}=s(2 s)^{2} \Rightarrow K_{s p}=4 s^{3}$
$4.5 \times 10^{-29}=4 s^{3}$
$1.125 \times 10^{-29}=s^{3}$
$\Rightarrow s=2.24 \times 10^{-10} \mathrm{M}$
Molarity of $\mathrm{Hg}_{2}^{2+}=s=2.24 \times 10^{-10} \mathrm{M}$
Molarity of $\mathrm{I}^{-}=2 s=4.48 \times 10^{-10} \mathrm{M}$
Question $68:$ The solubility product constant of $\mathrm{Ag}_{2} \mathrm{CrO}_{4}$ and $\mathrm{AgBr}$ are $1.1 \times 10^{-12}$ and $5.0 \times 10^{-13}$ respectively. Calculate the ratio of the molarities of their saturated solutions.
Solution. Let $s$ be the solubility of $\mathrm{Ag}_{2} \mathrm{CrO}_{4}$
Then, $\mathrm{Ag}_{2} \mathrm{CrO}_{4} \longleftrightarrow \mathrm{Ag}^{2+}+2 \mathrm{CrO}_{4}^{-}$
$K_{s p}=(2 s)^{2} . s=4 s^{3}$
$1.1 \times 10^{-12}=4 s^{3}$
$s=6.5 \times 10^{-5} \mathrm{M}$
Let $s^{\prime}$ be the solubility of $\mathrm{AgBr}$.
$\mathrm{AgBr}_{(s)} \longleftrightarrow \mathrm{Ag}^{+}+\mathrm{Br}^{-}$
$K_{s p}=s^{\prime 2}=5.0 \times 10^{-13}$
$\therefore s^{\prime}=7.07 \times 10^{-7} \mathrm{M}$
Therefore, the ratio of the molarities of their saturated solution is
$\frac{s}{s^{\prime}}=\frac{6.5 \times 10^{-5} \mathrm{M}}{7.07 \times 10^{-7} \mathrm{M}}=91.9$
Question $69:$ Equal volumes of $0.002 \mathrm{M}$ solutions of sodium iodate and cupric chlorate are mixed together. Will it lead to precipitation of copper iodate? (For cupric iodate $K_{\mathrm{sp}}=7.4 \times 10^{-8}$ ).
Solution. When equal volumes of sodium iodate and cupric chlorate solutions are mixed together, then the molar concentrations of both solutions are reduced to half i.e., $0.001 \mathrm{M}$.
Then,
Now, the solubility equilibrium for copper iodate can be written as:
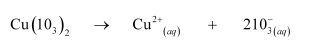
Ionic product of copper iodate:
$=\left[\mathrm{Cu}^{2+}\right]\left[10_{3}^{-}\right]^{2}$
$=(0.001)(0.001)^{2}$
$=1 \times 10^{-9}$
Since the ionic product $\left(1 \times 10^{-9}\right)$ is less than $K_{s p}\left(7.4 \times 10^{-8}\right)$, precipitation will not occur.
Question 70: The ionization constant of benzoic acid is $6.46 \times 10^{-5}$ and $K_{\mathrm{sp}}$ for silver benzoate is $2.5 \times 10^{-13}$. How many times is silver benzoate more soluble in a buffer of $\mathrm{pH} 3.19$ compared to its solubility in pure water?
Solution. Since $\mathrm{pH}=3.19$
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=6.46 \times 10^{-4} \mathrm{M}$
$\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}+\mathrm{H}_{2} \mathrm{O} \longleftrightarrow \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}+\mathrm{H}_{3} \mathrm{O}$
$K_{a} \frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}\right]}$
$\frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{a}}=\frac{6.46 \times 10^{-4}}{6.46 \times 10^{-5}}=10$
Let the solubility of $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOAg}$ be $\times \mathrm{mol} / \mathrm{L}$.
Then,
$\left[\mathrm{Ag}^{+}\right]=x$
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}\right]+\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]=x$
$10\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]+\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]=x$
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]=\frac{x}{11}$
$K_{s p}\left[\mathrm{Ag}^{+}\right]\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}\right]$
$2.5 \times 10^{-13}=x\left(\frac{x}{11}\right)$
$x=1.66 \times 10^{-6} \mathrm{~mol} / \mathrm{L}$
Thus, the solubility of silver benzoate in a $\mathrm{pH} 3.19$ solution is $1.66 \times 10^{-6} \mathrm{~mol} / \mathrm{L}$.
Now, let the solubility of $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOAg}$ be $\mathrm{x}^{\prime} \mathrm{mol} / \mathrm{L}$.
Then, $\left[\mathrm{Ag}^{+}\right]=x^{\prime} \mathrm{M}$ and $\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]=x^{\prime} \mathrm{M}$.
$K_{s p}=\left[\mathrm{Ag}^{+}\right]\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]$
$K_{s p}=\left(x^{\prime}\right)^{2}$
$x^{\prime}=\sqrt{K_{s p}}=\sqrt{2.5 \times 10^{-13}}=5 \times 10^{-7} \mathrm{~mol} / \mathrm{L}$
$\therefore \frac{x}{x^{\prime}}=\frac{1.66 \times 10^{-6}}{5 \times 10^{-7}}=3.32$
Hence, $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOAg}$ is approximately $3.317$ times more soluble in a low $\mathrm{pH}$ solution.
Question 71: What is the maximum concentration of equimolar solutions of ferrous sulphate and sodium sulphide so that when mixed in equal volumes, there is no precipitation of iron sulphide? (For iron sulphide, $K_{\text {sp }}=6.3 \times 10^{-18}$ )
Solution. Let the maximum concentration of each solution be $x \mathrm{~mol} / \mathrm{L} .$ After mixing, the volume of the concentrations of each solution will be reduced to half i.e., $\frac{x}{2}$
$\therefore\left[\mathrm{FeSO}_{4}\right]=\left[\mathrm{Na}_{2} \mathrm{~S}\right]=\frac{x}{2} \mathrm{M}$
Then, $\left[\mathrm{Fe}^{2+}\right]=\left[\mathrm{FeSO}_{4}\right]=\frac{x}{2} \mathrm{M}$
Also, $\left[\mathrm{S}^{2-}\right]=\left[\mathrm{Na}_{2} \mathrm{~S}\right]=\frac{x}{2} \mathrm{M}$
$\mathrm{FeS}_{(s)} \longleftrightarrow \mathrm{Fe}_{(a q)}^{2+}+\mathrm{S}_{(a q)}^{2-}$
$K_{s p}=\left[\mathrm{Fe}^{2+}\right]\left[\mathrm{S}^{2-}\right]$
$6.3 \times 10^{-18}=\left(\frac{x}{2}\right)\left(\frac{x}{2}\right)$
$\frac{x^{2}}{4}=6.3 \times 10^{-18}$
$\Rightarrow x=5.02 \times 10^{-9}$
If the concentrations of both solutions are equal to or less than $5.02 \times 10^{-9} \mathrm{M}$, then there will be no precipitation of iron sulphide.
Question $72$ : What is the minimum volume of water required to dissolve $1 \mathrm{~g}$ of calcium sulphate at $298 \mathrm{~K} ?$ (For calcium sulphate, $K_{\mathrm{sp}}$ is $\left.9.1 \times 10^{-6}\right)$
Solution. $\mathrm{CaSO}_{4(s)} \longleftrightarrow \mathrm{Ca}^{2+}{(a q)}+\mathrm{SO}_{4}^{2-}(a q)$
$K_{s p}=\left[\mathrm{Ca}^{2+}\right]\left[\mathrm{SO}_{4}^{2-}\right]$
Let the solubility of $\mathrm{CaSO}_{4}$ be $s$.
Then, $K_{s p}=s^{2}$
$9.1 \times 10^{-6}=s^{2}$
$s=3.02 \times 10^{-3} \mathrm{~mol} / \mathrm{L}$
Molecular mass of $\mathrm{CaSO}_{4}=136 \mathrm{~g} / \mathrm{mol}$
Solubility of $\mathrm{CaSO}_{4}$ in gram $/ \mathrm{L}=3.02 \times 10^{-3} \times 136$
$=0.41 \mathrm{~g} / \mathrm{L}$
This means that we need $1 \mathrm{~L}$ of water to dissolve $0.41 \mathrm{~g}$ of $\mathrm{CaSO}_{4}$
Therefore, to dissolve $1 \mathrm{~g}$ of $\mathrm{CaSO}_{4}$ we require $=\frac{1}{0.41} \mathrm{~L}=2.44 \mathrm{~L}$ of water.
Question 73: The concentration of sulphide ion in $0.1 \mathrm{M} \mathrm{HCl}$ solution saturated with hydrogen sulphide is $1.0 \times 10^{-19} \mathrm{M}$. If $10 \mathrm{~mL}$ of this is added to $5 \mathrm{~mL}$ of $0.04 \mathrm{M}$ solution of the following:
$\mathrm{FeSO}_{4}, \mathrm{MnCl}_{2}, \mathrm{ZnCl}_{2}$ and $\mathrm{CdCl}_{2}$. in which of these solutions precipitation will take place?
Given $K_{x p}$ for $\mathrm{FeS}=6.3 \times 10^{-18}, \mathrm{MnS}=2.5 \times 10^{-13}, \mathrm{ZnS}=1.6 \times 10^{-2+}$
$\mathrm{CdS}=8.0 \times 10^{-27}$
Solution. For precipitation to take place, it is required that the calculated ionic product exceeds the $K_{s p}$ value.
Before mixing:
$\left[\mathrm{S}^{2-}\right]=1.0 \times 10^{-19} \mathrm{M}\left[\mathrm{M}^{2+}\right]=0.04 \mathrm{M}$
volume $=10 \mathrm{~mL} \quad$ volume $=5 \mathrm{~mL}$
After mixing:
$\begin{array}{ll}{\left[\mathrm{S}^{2-}\right]=?} & {\left[\mathrm{M}^{2+}\right]=?} \\ \text { volume }=(10+5)=15 \mathrm{~mL} & \text { volume }=15 \mathrm{~mL}\end{array}$
volume $=(10+5)=15 \mathrm{~mL} \quad$ volume $=15 \mathrm{~mL}$
$\left[\mathrm{S}^{2-}\right]=\frac{1.0 \times 10^{-19} \times 10}{15}=6.67 \times 10^{-20} \mathrm{M}$
$\left[\mathrm{M}^{2+}\right]=\frac{0.04 \times 5}{15}=1.33 \times 10^{-2} \mathrm{M}$
Ionic product $=\left[\mathrm{M}^{2+}\right]\left[\mathrm{S}^{2-}\right]$
$=\left(1.33 \times 10^{-2}\right)\left(6.67 \times 10^{-20}\right)$
$=8.87 \times 10^{-22}$
This ionic product exceeds the $K_{s p}$ of Zns and CdS. Therefore, precipitation will occur in $\mathrm{CdCl}_{2}$ and $\mathrm{ZnCl}_{2}$ solutions.
So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.
Also Read,
Class 11 Chemistry Notes Download.
Class 11 Chemistry Book Chapterwise Download.
Class 11 Chemistry Exemplar Chapterwise Download.
If you have any Confusion related to NCERT Solutions for Class 11 Chemistry chapter 7 Equilibrium PDF then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 11 Chemistry by Kota’s top IITian’s Faculties Install the eSaral App
