NCERT Solutions for Class 11 Chemistry chapter 4 Chemical Bonding and Molecular Structure PDF

Hey, are you a class 11 student and looking for ways to download NCERT Solutions for NCERT Solutions for Class 11 Chemistry chapter 4 Chemical Bonding and Molecular Structure PDF? If yes. Then read this post till the end.

In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 4 Chemical Bonding and Molecular Structure PDF that are prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

If you want to learn and understand class 11 Chemistry chapter 4 "Chemical Bonding and Molecular Structure" in an easy way then you can use these solutions PDF.

NCERT Solutions helps students to Practice important concepts of subjects easily. Class 11 Chemistry solutions provide detailed explanations of all the NCERT questions that students can use to clear their doubts instantly.

If you want to score high in your class 11 Chemistry Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.

In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 4 Chemical Bonding and Molecular Structure PDF that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

Download NCERT Solutions for Class 11 Chemistry chapter 4 Chemical Bonding and Molecular Structure PDF

Question 1: Explain the formation of a chemical bond.

Solution. A chemical bond is defined as an attractive force that holds the constituents (atoms, ions etc.) together in a chemical species.

Various theories have been suggested for the formation of chemical bonds such as the electronic theory, valence shell electron pair repulsion theory, valence bond theory, and molecular orbital theory.

each other and complete their respective octets or duplets to attain the stable configuration of the nearest noble gases. This combination can occur either by sharing of electrons or by transferring one or more electrons from one atom to another. The chemical bond formed as a result of sharing of electrons between atoms is called a covalent bond. An ionic bond is formed as a result of the transference of electrons from one atom to another

Question 2: Write Lewis dot symbols for atoms of the following elements: $\mathrm{Mg}, \mathrm{Na}, \mathrm{B}, \mathrm{O}, \mathrm{N}, \mathrm{Br}$.

Solution. Mg: There are two valence electrons in $\mathrm{Mg}$ atom. Hence, the Lewis dot symbol for $\mathrm{Mg}$ is: $\ddot{\mathrm{M}}_{\mathrm{g}}$

Na: There is only one valence electron in an atom of sodium. Hence, the Lewis dot structure is: Na-

B: There are 3 valence electrons in Boron atom. Hence, the Lewis dot structure is: $\cdot$ B.

Q: There are six valence electrons in an atom of oxygen. Hence, the Lewis dot structure is: :0:

$\underline{N}$ : There are five valence electrons in an atom of nitrogen. Hence, the Lewis dot structure is: $: \ddot{\mathrm{N}}$.

$\mathrm{Br}$ : There are seven valence electrons in bromine. Hence, the Lewis dot structure is: $: \ddot{\mathrm{Br}}$ :

Question 3: Write Lewis symbols for the following atoms and ions:

$\mathrm{S}$ and $\mathrm{S}^{2-} ; \mathrm{Al}$ and $\mathrm{Al}^{3+} ; \mathrm{H}$ and $\mathrm{H}^{-}$

Solution. \text { (i) } \mathrm{S} \text { and } \mathrm{S}^{2-}

The number of valence electrons in sulphur is 6 .

The dinegative charge infers that there will be two electrons more in addition to the six valence electrons. Hence, the Lewis dot symbol of $\mathrm{S}^{2-}$ is $[\ddot{\therefore}::]$

(ii) $\mathrm{Al}$ and $\mathrm{Al}^{3+}$

The number of valence electrons in aluminium is $3 .$

The Lewis dot symbol of aluminium (AI) is $^{\circ} \cdot$

The tripositive charge on a species infers that it has donated its three electrons. Hence, the Lewis dot symbol is $[\mathrm{Al}]^{3+}$

(iii) $\mathrm{H}$ and $\mathrm{H}^{-}$

The number of valence electrons in hydrogen is 1.

The Lewis dot symbol of hydrogen $(\mathrm{H})$ is $\mathrm{H} \cdot$.

The uninegative charge infers that there will be one electron more in addition to the one valence electron. Hence, the Lewis dot symbol is $[\ddot{H}]^{-}$

Question 4: Draw the Lewis structures for the following molecules and ions:

$\mathrm{H}_{2} \mathrm{~S}, \mathrm{SiCl}_{4}, \mathrm{BeF}_{2}, \mathrm{CO}_{3}^{2-}, \mathrm{HCOOH}$

Solution. $\mathrm{H}_{2} \mathrm{~S}$



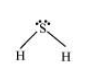
$\mathrm{SiCl}_{4}$



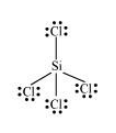
BeF $_{2}$



$\mathrm{CO}_{3}^{2-}$



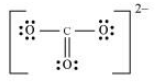
HCOOH



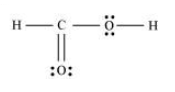
Question 5: Define octet rule. Write its significance and limitations.

Solution. The octet rule or the electronic theory of chemical bonding was developed by Kossel and Lewis. According to this rule, atoms can combine either by transfer of valence electrons from one atom to another or by sharing their valence electrons in order to attain the nearest noble gas configuration by having an octet in their valence shell.



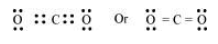
The octet rule successfully explained the formation of chemical bonds depending upon the nature of the element.

Limitations of the octet theory:

The following are the limitations of the octet rule:

(a) The rule failed to predict the shape and relative stability of molecules.

(b) It is based upon the inert nature of noble gases. However, some noble gases like xenon and krypton form compounds such as $\mathrm{XeF}_{2}, \mathrm{KrF}_{2}$ etc.

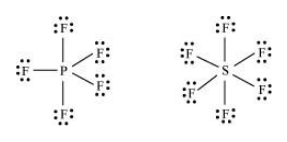
(c) The octet rule cannot be applied to the elements in and beyond the third period of the periodic table. The elements present in these periods have more than eight valence electrons around the central atom. For example: $\mathrm{PF}_{5}, \mathrm{SF}_{6,}$ etc.



(d) The octet rule is not satisfied for all atoms in a molecule having an odd number of electrons. For example, $\mathrm{NO}$ and $\mathrm{NO}_{2}$ do not satisfy the octet rule.



Question 6: Write the favourable factors for the formation of ionic bond.

Solution. neutral atoms can lose or gain electrons. Bond formation also depends upon the lattice energy of the compound formed.

Hence, favourable factors for ionic bond formation are as follows:

(i) Low ionization enthalpy of metal atom.

(ii) High electron gain enthalpy $\left(\Delta_{e g} H\right)$ of a non-metal atom.

(iii) High lattice energy of the compound formed.

Question 7: Discuss the shape of the following molecules using the VSEPR model:

$\mathrm{BeCl}_{2}, \mathrm{BCl}_{3}, \mathrm{SiCl}_{4}, \mathrm{AsF}_{5}, \mathrm{H}_{2} \mathrm{~S}, \mathrm{PH}_{3}$

Solution. $\mathrm{BeCl}_{2}$

$\mathrm{Cl}: \mathrm{Be}: \mathrm{Cl}$

The central atom has no lone pair and there are two bond pairs. i.e., $\mathrm{BeCl}_{2}$ is of the type $\mathrm{AB}_{2}$. Hence, it has a linear shape.

$\mathrm{BCl}_{3}:$



The central atom has no lone pair and there are three bond pairs. Hence, it is of the type $\mathrm{AB}_{3}$. Hence, it is trigonal planar.



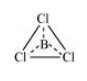
$\mathrm{SiCl}_{4}$



The central atom has no lone pair and there are four bond pairs. Hence, the shape of $\mathrm{SiCl}_{4}$ is tetrahedral being the $\mathrm{AB}_{4}$ type molecule.

$\mathrm{AsF}_{5}$ :



The central atom has no lone pair and there are five bond pairs. Hence, $A s F_{5}$ is of the type $A B_{5}$. Therefore, the shape is_trigonal bipyramidal.

$\mathrm{H}_{2} \mathrm{~S}:$



The central atom has one lone pair and there are two bond pairs. Hence, $\mathrm{H}_{2} \mathrm{~S}$ is of the type $\mathrm{AB}_{2} \mathrm{E}$. The shape is Bent.

$\mathrm{PH}_{3}:$



The central atom has one lone pair and there are three bond pairs. Hence, $\mathrm{PH}_{3}$ is of the $\mathrm{AB}_{3} \mathrm{E}$ type. Therefore, the shape is trigonal pyramidal.

Question 8: Although geometries of $\mathrm{NH}_{3}$ and $\mathrm{H}_{2} \mathrm{O}$ molecules are distorted tetrahedral, bond angle in water is less than that of ammonia. Discuss.

Solution. The molecular geometry of $\mathrm{NH}_{3}$ and $\mathrm{H}_{2} \mathrm{O}$ can be shown as:



The central atom ( $\mathrm{N}$ ) in $\mathrm{NH}_{3}$ has one lone pair and there are three bond pairs. In $\mathrm{H}_{2} \mathrm{O}$, there are two lone pairs and two bond pairs.

The two lone pairs present in the oxygen atom of $\mathrm{H}_{2} \mathrm{O}$ molecule repels the two bond pairs. This repulsion is stronger than the repulsion between the lone pair and the three bond pairs on the nitrogen atom.

Since the repulsions on the bond pairs in $\mathrm{H}_{2} \mathrm{O}$ molecule are greater than that in $\mathrm{NH}_{3}$, the bond angle in water is less than that of ammonia.

Question 9: How do you express the bond strength in terms of bond order?

Solution. Bond strength represents the extent of bonding between two atoms forming a molecule. The larger the bond energy, the stronger is the bond and the greater is the bond order.

Question 10: Define the bond length.

Solution. Bond length is defined as the equilibrium distance between the nuclei of two bonded atoms in a molecule. Bond lengths are expressed in terms of Angstrom $\left(10^{-10} \mathrm{~m}\right)$ or picometer

Bond lengths are expressed in terms of Angstrom $\left(10^{-10} \mathrm{~m}\right)$ or picometer

$\left(10^{-12} \mathrm{~m}\right)$ and are measured by spectroscopic X-ray diffractions and electron-diffraction techniques.

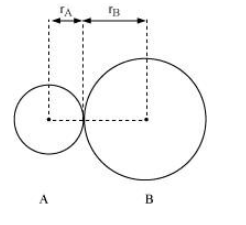
In an ionic compound, the bond length is the sum of the ionic radii of the constituting atoms $\left(d=r_{+}+r_{-}\right) .$ In a covalent compound, it is the sum of their covalent radii $\left(d=r_{\mathrm{A}}+r_{\mathrm{B}}\right)$



Question 11: Explain the important aspects of resonance with reference to the $\mathrm{CO}_{3}^{2-}$ ion.

Solution. According to experimental findings, all carbon to oxygen bonds in $\mathrm{CO}_{3}^{2-}$ are equivalent. Hence, it is inadequate to represent $\mathrm{CO}_{3}^{2-}$ ion by a single Lewis structure having two single bonds and one double bond.

Therefore, carbonate ion is described as a resonance hybrid of the following structures:



Question 12: $\mathrm{H}_{3} \mathrm{PO}_{3}$ can be represented by structures 1 and 2 shown below. Can these two structures be taken as the canonical forms of the resonance hybrid representing $\mathrm{H}_{3} \mathrm{PO}_{3} ?$ If not, give reasons for the same.



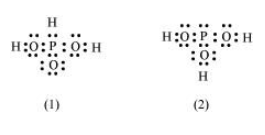
Solution. The given structures cannot be taken as the canonical forms of the resonance hybrid of $\mathrm{H}_{3} \mathrm{PO}_{3}$ because the positions of the atoms have changed.

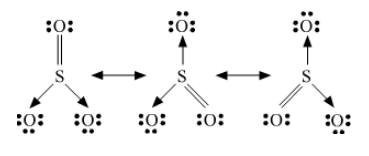
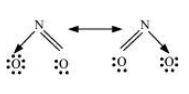
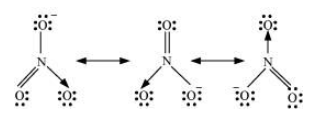
Question 13: Write the resonance structures for $\mathrm{SO}_{3}, \mathrm{NO}_{2}$ and $\mathrm{NO}_{3}^{-}$.

Solution. The resonance structures are:

(a) $\mathrm{SO}_{3}$.



(b) $\mathrm{NO}_{2}$ :



(c) $\mathrm{NO}_{3}^{-}$ :



Question 14: Use Lewis symbols to show electron transfer between the following atoms to form cations and anions: (a) $\mathrm{K}$ and $\mathrm{S}$ (b) $\mathrm{Ca}$ and $\mathrm{O}$ (c) $\mathrm{Al}$ and $\mathrm{N}$.

Solution. (a) $\mathrm{K}$ and $\mathrm{S}$.

The electronic configurations of $\mathrm{K}$ and $\mathrm{S}$ are as follows:

$\mathrm{K}: 2,8,8,1$

$S: 2,8,6$



Sulphur (S) requires 2 more electrons to complete its octet. Potassium (K) requires one electron more than the nearest noble gas i.e., Argon. Hence, the electron transfer can be shown as:



(b) $\underline{\text { Ca and }} \mathrm{O}$ :

The electronic configurations of $\mathrm{Ca}$ and $\mathrm{O}$ are as follows:

Ca: $2,8,8,2$

$\mathrm{O}: 2,6$

Oxygen requires two electrons more to complete its octet, whereas calcium has two electrons more than the nearest noble gas i.e., Argon. Hence, the electron transfer takes place as:



(c) $\mathrm{Al}$ and $\mathrm{N}$ :

The electronic configurations of $\mathrm{Al}$ and $\mathrm{N}$ are as follows:

Al: $2,8,3$

$\mathrm{N}: 2,5$

Nitrogen is three electrons short of the nearest noble gas (Neon), whereas aluminium has three electrons more than Neon. Hence, the electron transference can be shown as:



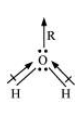
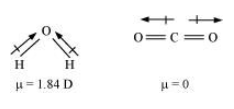
Question 15: Although both $\mathrm{CO}_{2}$ and $\mathrm{H}_{2} \mathrm{O}$ are triatomic molecules, the shape of $\mathrm{H}_{2} \mathrm{O}$ molecule is bent while that of $\mathrm{CO}_{2}$ is linear. Explain this on the basis of dipole moment.

Solution. According to experimental results, the dipole moment of carbon dioxide is zero. This is possible only if the molecule is linear so that the dipole moments of $\mathrm{C}-\mathrm{O}$ bonds are equal and opposite to nullify each other.



Resultant $\mu=0 \mathrm{D}$

$\mathrm{H}_{2} \mathrm{O}$, on the other hand, has a dipole moment value of $1.84 \mathrm{D}$ (though it is a triatomic molecule as $\mathrm{CO}_{2}$ ). The value of the dipole moment suggests that the structure of $\mathrm{H}_{2} \mathrm{O}$ molecule is bent where the dipole moment of O-H bonds are unequal.



Question 16: Write the significance/applications of dipole moment.

Solution. In heteronuclear molecules, polarization arises due to a difference in the electronegativities of the constituents of atoms. As a result, one end of the molecule acquires a The product of the magnitude of the charge and the distance between the centres of positive-negative charges is called the dipole moment $(\mu)$ of the molecule. It is a vector quantity and is represented by an arrow with its tail at the positive centre and head pointing towards a negative centre.

Dipole moment $(\mu)=$ charge $(\mathrm{Q}) \times$ distance of separation $(r)$

The SI unit of a dipole moment is 'esu'.

1 esu $=3.335 \times 10^{-30} \mathrm{Cm}$

Dipole moment is the measure of the polarity of a bond. It is used to differentiate between polar and non-polar bonds since all non-polar molecules (e.g. $\mathrm{H}_{2}, \mathrm{O}_{2}$ ) have zero dipole moments. It is also helpful in calculating the percentage ionic character of a molecule.



Question 17: Define electronegativity. How does it differ from electron gain enthalpy?

Solution. Electronegativity is the ability of an atom in a chemical compound to attract a bond pair of electrons towards itself.

Electronegativity of any given element is not constant. It varies according to the element to which it is bound. It is not a measurable quantity. It is only a relative number.

On the other hand, electron gain enthalpy is the enthalpy change that takes place when an electron is added to a neutral gaseous atom to form an anion. It can be negative or positive depending upon whether the electron is added or removed. An element has a constant value of the electron gain enthalpy that can be measured experimentally.

Question 18: Explain with the help of suitable example polar covalent bond.

Solution. When two dissimilar atoms having different electronegativities combine to form a covalent bond, the bond pair of electrons is not shared equally. The bond pair shifts towards the nucleus of the atom having greater electronegativity. As a result, electron distribution gets distorted and the electron cloud is displaced towards the electronegative atom.

As a result, the electronegative atom becomes slightly negatively charged while the other atom becomes slightly positively charged. Thus, opposite poles are developed in the molecule and this type of a bond is called a polar covalent bond.

$\mathrm{HCl}$, for example, contains a polar covalent bond. Chlorine atom is more electronegative than hydrogen atom. Hence, the bond pair lies towards chlorine and therefore, it acquires a partial negative charge.



Question 19: Arrange the bonds in order of increasing ionic character in the molecules: $\mathrm{LiF}, \mathrm{K}_{2} \mathrm{O}, \mathrm{N}_{2}, \mathrm{SO}_{2}$ and $\mathrm{CIF}_{3}$

Solution. The ionic character in a molecule is dependent upon the electronegativity difference between the constituting atoms. The greater the difference, the greater will be the ionic character of the molecule.

On this basis, the order of increasing ionic character in the given molecules is

$\mathrm{N}_{2}<\mathrm{SO}_{2}<\mathrm{CIF}_{3}<\mathrm{K}_{2} \mathrm{O}<\mathrm{LiF}$

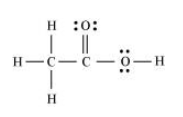
Question 20: The skeletal structure of $\mathrm{CH}_{3} \mathrm{COOH}$ as shown below is correct, but some of the bonds are shown incorrectly. Write the correct Lewis structure for acetic acid.

Solution. The correct Lewis structure for acetic acid is as follows:



Question 21: Apart from tetrahedral geometry, another possible geometry for $\mathrm{CH}_{4}$ is square planar with the four $\mathrm{H}$ atoms at the corners of the square and the $\mathrm{C}$ atom at its centre. Explain why $\mathrm{CH}_{4}$ is not square planar?

Solution. Electronic configuration of carbon atom:

${ }_{6} \mathrm{C}: 1 \mathrm{~s}^{2} 2 s^{2} 2 p^{2}$

In the excited state, the orbital picture of carbon can be represented as:



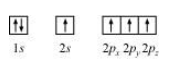
Hence, carbon atom undergoes $s p^{3}$ hybridization in $\mathrm{CH}_{4}$ molecule and takes a tetrahedral shape.



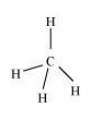
For a square planar shape, the hybridization of the central atom has to be $d s p^{2}$. However, an atom of carbon does not have $d$ -orbitalsto undergo $d s p^{2}$ hybridization. Hence, the structure of $\mathrm{CH}_{4}$ cannot be square planar.

Moreover, with a bond angle of $90^{\circ}$ in square planar, the stability of $\mathrm{CH}_{4}$ will be very less because of the repulsion existing between the bond pairs. Hence, VSEPR theory also supports a tetrahedral structure for $\mathrm{CH}_{4}$.

Question 22: Explain why $\mathrm{BeH}_{2}$ molecule has a zero dipole moment although the $\mathrm{Be}-\mathrm{H}$ bonds are polar.

Solution. The Lewis structure for $\mathrm{BeH}_{2}$ is as follows:

$\mathrm{H}: \mathrm{Be}: \mathrm{H}$

There is no lone pair at the central atom (Be) and there are two bond pairs. Hence, $\mathrm{BeH}_{2}$ is of the type $\mathrm{AB}_{2}$. It has a linear structure.



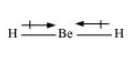
Dipole moments of each H-Be bond are equal and are in opposite directions. Therefore, they nullify each other. Hence, $\mathrm{BeH}_{2}$ molecule has zero dipole moment.

Question 23: Which out of $\mathrm{NH}_{3}$ and $\mathrm{NF}_{3}$ has higher dipole moment and why?

Solution. In both molecules i.e., $\mathrm{NH}_{3}$ and $\mathrm{NF}_{3}$, the central atom (N) has a lone pair electron and there are three bond pairs. Hence, both molecules have a pyramidal shape. Since fluorine is more electronegative than hydrogen, it is expected that the net dipole moment of $\mathrm{NF}_{3}$ is greater than $\mathrm{NH}_{3}$. However, the net dipole moment of $\mathrm{NH}_{3}(1.46 \mathrm{D})$ is greater than that of $\mathrm{NF}_{3}(0.24 \mathrm{D})$.

This can be explained on the basis of the directions of the dipole moments of each individual bond in $\mathrm{NF}_{3}$ and $\mathrm{NH}_{3}$. These directions can be shown as



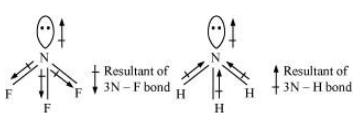
Thus, the resultant moment of the $\mathrm{N}-\mathrm{H}$ bonds add up to the bond moment of the lone pair (the two being in the same direction), whereas that of the three $\mathrm{N}-\mathrm{F}$ bonds partly cancels the moment of the lone pair

Hence, the net dipole moment of $\mathrm{NF}_{3}$ is less than that of $\mathrm{NH}_{3}$.

Question 24: What is meant by hybridisation of atomic orbitals? Describe the shapes of $s p, s p^{2}, s p^{3}$ hybrid orbitals.

Solution. Hybridization is defined as an intermixing of a set of atomic orbitals of slightly different energies, thereby forming a new set of orbitals having equivalent energies and shapes.

For example, one 2 s-orbital hybridizes with two $2 p$ -orbitals of carbon to form three new $s p^{2}$ hybrid orbitals.

These hybrid orbitals have minimum repulsion between their electron pairs and thus, are more stable. Hybridization helps indicate the geometry of the molecule

Shape of sp hybrid orbitals: sp hybrid orbitals have a linear shape. They are formed by the intermixing of $s$ and $p$ orbitals as



Shape of $s p^{2}$ hybrid orbitals:

$s p^{2}$ hybrid orbitals are formed as a result of the intermixing of one s-orbital and two $2 p$ -orbitals. The hybrid orbitals are oriented in a trigonal planar arrangement as:



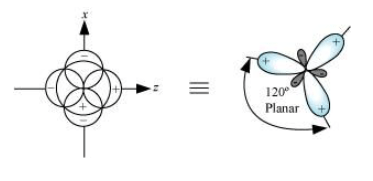
Shape of $s p^{3}$ hybrid orbitals:

Four $s p^{3}$ hybrid orbitals are formed by intermixing one s-orbital with three $p$ -orbitals. The four $s p^{3}$ hybrid orbitals are arranged in the form of a tetrahedron as:



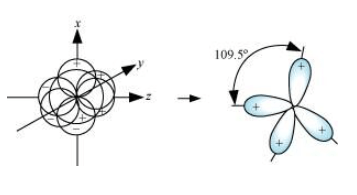
Question 25: Describe the change in hybridisation (if any) of the Al atom in the following reaction.

$\mathrm{AlCl}_{3}+\mathrm{Cl}^{-} \longrightarrow \mathrm{AlCl}_{4}^{-}$

Solution. The valence orbital picture of aluminium in the ground state can be represented as:



The orbital picture of aluminium in the excited state can be represented as:



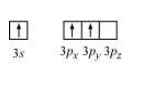
Hence, it undergoes $s p^{2}$ hybridization to give a trigonal planar arrangement (in $\mathrm{AlCl}_{3}$ ).

To form $\mathrm{AlCl}_{4}^{-}$, the empty $3 p_{\mathrm{z}}$ orbital also gets involved and the hybridization changes from $s p^{2}$ to $s p^{3} .$ As a result, the shape gets changed to tetrahedral.

Question 26: Is there any change in the hybridisation of $B$ and $N$ atoms as a result of the following reaction?

$\mathrm{BF}_{3}+\mathrm{NH}_{3} \rightarrow \mathrm{F}_{3} \mathrm{~B} \cdot \mathrm{NH}_{3}$

Solution. Boron atom in $\mathrm{BF}_{3}$ is $s p^{2}$ hybridized. The orbital picture of boron in the excited state can be shown as:



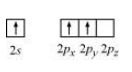
Nitrogen atom in $\mathrm{NH}_{3}$ is $s p^{3}$ hybridized. The orbital picture of nitrogen can be represented as:



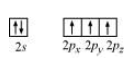
After the reaction has occurred, an adduct $\mathrm{F}_{3} \mathrm{~B} \cdot \mathrm{NH}_{3}$ is formed as hybridization of ' $\mathrm{B}$ ' changes to $s p^{3}$. However, the hybridization of ' $\mathrm{N}$ ' remains intact.

Question 27: Draw diagrams showing the formation of a double bond and a triple bond between carbon atoms in $\mathrm{C}_{2} \mathrm{H}_{4}$ and $\mathrm{C}_{2} \mathrm{H}_{2}$ molecules

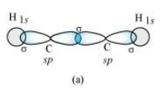
Solution. $\mathrm{C}_{2} \mathrm{H}_{4}:$

The electronic configuration of $\mathrm{C}$ -atom in the excited state is:

${ }_{6} \mathrm{C}=1 s^{2} 2 s^{\prime} 2 p_{x}^{\prime} 2 p_{y}^{\prime} 2 p_{z}^{\prime}$

In the formation of an ethane molecule $\left(\mathrm{C}_{2} \mathrm{H}_{4}\right)$, one $s p^{2}$ hybrid orbital of carbon overlaps a $s p^{2}$ hybridized orbital of another carbon atom, thereby forming a $\mathrm{C}-\mathrm{C}$ sigma bond.

The remaining two $s p^{2}$ orbitals of each carbon atom form a $s p^{2}-s$ sigma bond with two hydrogen atoms. The unhybridized orbital of one carbon atom undergoes sidewise overlap with the orbital of a similar kind present on another carbon atom to form a weak $\Pi$ -bond.



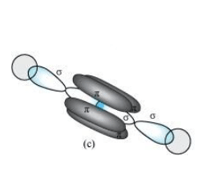
$\mathrm{C}_{2} \mathrm{H}_{2}:$

In the formation of $\mathrm{C}_{2} \mathrm{H}_{2}$ molecule, each C-atom is sp hybridized with two $2 p$ -orbitals in an unhybridized state.

One sp orbital of each carbon atom overlaps with the other along the internuclear axis forming a C-C sigma bond. The second sp orbital of each C-atom overlaps a half-filled 1 s-orbital to form a $\sigma$ bond

The two unhybridized $2 p$ -orbitals of the first carbon undergo sidewise overlap with the $2 p$ orbital of another carbon atom, thereby forming two pi ( $\pi)$ bonds between carbon atoms. Hence, the triple bond between two carbon atoms is made up of one sigma and two m-bonds.







Question 28: What is the total number of sigma and pi bonds in the following molecules?

(a) $\mathrm{C}_{2} \mathrm{H}_{2}$ (b) $\mathrm{C}_{2} \mathrm{H}_{4}$

Solution. A single bond is a result of the axial overlap of bonding orbitals. Hence, it contributes a sigma bond. A multiple bond (double or triple bond) is always formed as a result of the sidewise overlap of orbitals. A pi-bond is always present in it. A triple bond is a combination of two pi-bonds and one sigma bond.

Structure of $\mathrm{C}_{2} \mathrm{H}_{2}$ can be represented as:



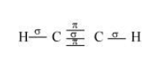
Hence, there are three sigma and two pi-bonds in $\mathrm{C}_{2} \mathrm{H}_{2}$.

The structure of $\mathrm{C}_{2} \mathrm{H}_{4}$ can be represented as:



Hence, there are five sigma bonds and one pi-bond in $\mathrm{C}_{2} \mathrm{H}_{4}$.

Question 29: Considering $x$ -axis as the internuclear axis which out of the following will not form a sigma bond and why? (a) $1 s$ and $1 s$ (b) $1 s$ and $2 p_{x}$ (c) $2 p_{y}$ and $2 p_{y}$ (d) $1 s$ and $2 s$.

Solution. $2 p_{y}$ and $2 p_{y}$ orbitals will not a form a sigma bond. Taking $x$ -axis as the internuclear axis, $2 p_{y}$ and $2 p_{y}$ orbitals will undergo lateral overlapping, thereby forming a pi (\Pi) bond.

Question 30: Which hybrid orbitals are used by carbon atoms in the following molecules?

Solution. (a) $\mathrm{CH}_{3}-\mathrm{CH}_{3}$

(b) $\mathrm{CH}_{3}-\mathrm{CH}=\mathrm{CH}_{2}$

(c) $\mathrm{CH}_{3}-\mathrm{CH}_{2}-\mathrm{OH}$

(d) $\mathrm{CH}_{3}-\mathrm{CHO}$

(e) $\mathrm{CH}_{3} \mathrm{COOH}$

Solution.(a)



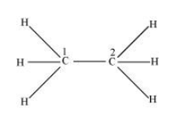
Both $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ are $s p^{3}$ hybridized.

(b)



$\mathrm{C}_{1}$ is $s p^{3}$ hybridized, while $\mathrm{C}_{2}$ and $\mathrm{C}_{3}$ are $s p^{2}$ hybridized.

(c)



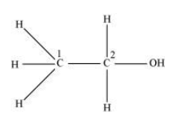
Both $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ are $s p^{3}$ hybridized.

(d)



$\mathrm{C}_{1}$ is $s p^{3}$ hybridized and $\mathrm{C}_{2}$ is $s p^{2}$ hybridized.

(e)



$\mathrm{C}_{1}$ is $s p^{3}$ hybridized and $\mathrm{C}_{2}$ is $s p^{2}$ hybridized.

Question 31: What do you understand by bond pairs and lone pairs of electrons? Illustrate by giving one example of each type.

Solution. When two atoms combine by sharing their one or more valence electrons, a covalent bond is formed between them.

The shared pairs of electrons present between the bonded atoms are called bond pairs. All valence electrons may not participate in bonding. The electron pairs that do not participate in bonding are called lone pairs of electrons.

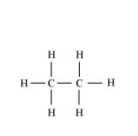
For example, in $\mathrm{C}_{2} \mathrm{H}_{6}$ (ethane), there are seven bond pairs but no lone pair present.



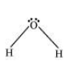
In $\mathrm{H}_{2} \mathrm{O}$, there are two bond pairs and two lone pairs on the central atom (oxygen).



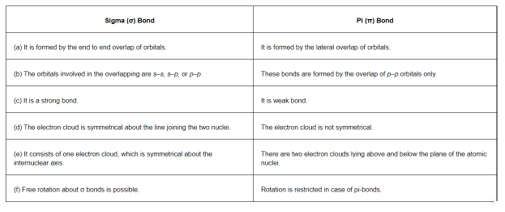
Question 32: Distinguish between a sigma and a pi bond.

Solution. The following are the differences between sigma and pi-bonds:



Question 33: Explain the formation of $\mathrm{H}_{2}$ molecule on the basis of valence bond theory.

Solution. Let us assume that two hydrogen atoms (A and B) with nuclei $\left(\mathrm{N}_{\mathrm{A}}\right.$ and $\left.\mathrm{N}_{\mathrm{B}}\right)$ and electrons $\left(\mathrm{e}_{\mathrm{A}}\right.$ and $\mathrm{e}_{\mathrm{B}}$ ) are taken to undergo a reaction to form a hydrogen molecule.

When $A$ and $B$ are at a large distance, there is no interaction between them. As they begin to approach each other, the attractive and repulsive forces start operating.

Attractive force arises between:

(a) Nucleus of one atom and its own electron i.e., $N_{A}-e_{A}$ and $N_{B}-e_{B}$.

(b) Nucleus of one atom and electron of another atom i.e., $N_{A}-e_{B}$ and $N_{B}-e_{A}$.

Repulsive force arises between:

(a) Electrons of two atoms i.e., $e_{A}-e_{B}$.

(b) Nuclei of two atoms i.e., $\mathrm{N}_{\mathrm{A}}-\mathrm{N}_{\mathrm{B}}$.

The force of attraction brings the two atoms together, whereas the force of repulsion tends to push them apart.





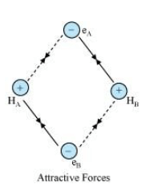
The magnitude of the attractive forces is more than that of the repulsive forces. Hence, the two atoms approach each other. As a result, the potential energy decreases. Finally, a state is reached when the attractive forces balance the repulsive forces and the system acquires minimum energy. This leads to the formation of a dihydrogen molecule.

Question 34: Write the important conditions required for the linear combination of atomic orbitals to form molecular orbitals.

Solution. The given conditions should be satisfied by atomic orbitals to form molecular orbitals:

(a) The combining atomic orbitals must have the same or nearly the same energy. This means that in a homonuclear molecule, the 1 s-atomic orbital of an atom can combine with the $1 \mathrm{~s}$ -atomic orbital of another atom, and not with the $2 \mathrm{~s}$ -orbital.

(b) The combining atomic orbitals must have proper orientations to ensure that the overlap is maximum.

(c) The extent of overlapping should be large.

Question 35: Use molecular orbital theory to explain why the $\mathrm{Be}_{2}$ molecule does not exist.

Solution. The electronic configuration of Beryllium is $1 s^{2} 2 s^{2}$.

The molecular orbital electronic configuration for $\mathrm{Be}_{2}$ molecule can be written as:

$\begin{array}{cccc}\sigma^{2} & \sigma^{*} & \sigma^{2} & \sigma^{* 2} \\ 1 s & 1 s & 2 s & 2 s\end{array}$

Hence, the bond order for $\mathrm{Be}_{2}$ is $\frac{1}{2}\left(N_{b}-N_{a}\right)$.

Where,

$N_{b}=$ Number of electrons in bonding orbitals

$N_{a}=$ Number of electrons in anti-bonding orbitals

$\therefore$ Bond order of $\mathrm{Be}_{2}=\frac{1}{2}(4-4)=0$

A negative or zero bond order means that the molecule is unstable. Hence, $\mathrm{Be}_{2}$ molecule does not exist.

Question 36: Compare the relative stability of the following species and indicate their magnetic properties;

$\mathrm{O}_{2}, \mathrm{O}_{2}^{+}, \mathrm{O}_{2}^{-}$ (superoxide), $\mathrm{O}_{2}^{2-}$ (peroxide)

Solution. There are 16 electrons in a molecule of dioxygen, 8 from each oxygen atom. The electronic configuration of oxygen molecule can be written as:



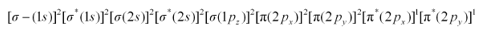
Since the 1 s orbital of each oxygen atom is not involved in boding, the number of bonding electrons $=8=N_{\mathrm{b}}$ and the number of anti-bonding orbitals $=4=N_{\mathrm{a}}$

Bond order $=\frac{1}{2}\left(N_{\mathrm{b}}-N_{\mathrm{a}}\right)$

$=\frac{1}{2}(8-4)$

$=2$

Similarly, the electronic configuration of $\mathrm{O}_{2}^{+}$ can be written as:



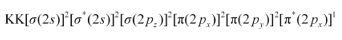
$N_{\mathrm{b}}=8$

$N_{\mathrm{a}}=3$

Bond order of $\mathrm{O}_{2}^{+}=\frac{1}{2}(8-3)$

$=2.5$

Electronic configuration of $\mathrm{O}_{2}^{-}$ ion will be:



$N_{\mathrm{b}}=8$

$N_{\mathrm{a}}=5$

Bond order of $\mathrm{O}_{2}^{-}=\frac{1}{2}(8-5)$

$=1.5$

Electronic configuration of $\mathrm{O}_{2}^{2-}$ ion will be:

$N_{\mathrm{b}}=8$

$N_{\mathrm{a}}=6$

Bond order of $\mathrm{O}_{2}^{2-}=\frac{1}{2}(8-6)$

$=1$

Bond dissociation energy is directly proportional to bond order. Thus, the higher the bond order, the greater will be the stability. On this basis, the order of stability is $\mathrm{O}_{2}^{+}>\mathrm{O}_{2}>\mathrm{O}_{2}^{-}>\mathrm{O}_{2}^{2}$

Question 37: Write the significance of a plus and a minus sign shown in representing the orbitals.

Solution. Molecular orbitals are represented by wave functions. A plus sign in an orbital indicates a positive wave function while a minus sign in an orbital represents a negative wave function.

Question 38: Describe the hybridisation in case of $\mathrm{PCl}_{5}$. Why are the axial bonds longer as compared to equatorial bonds?

Solution. The ground state and excited state outer electronic configurations of phosphorus $(Z=15)$ are:





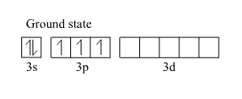
Phosphorus atom is $s p^{3} d$ hybridized in the excited state. These orbitals are filled by the electron pairs donated by five $\mathrm{Cl}$ atoms as:

$\mathrm{PCl}_{5}$



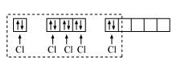
The five $s p^{3} d$ hybrid orbitals are directed towards the five corners of the trigonal bipyramidals. Hence, the geometry of $\mathrm{PCl}_{5}$ can be represented as:



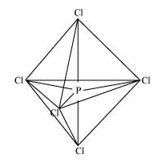
There are five $P-C l$ sigma bonds in $\mathrm{PCl}_{5}$. Three P-Cl bonds lie in one plane and make an angle of $120^{\circ}$ with each other. These bonds are called equatorial bonds.

The remaining two P-Cl bonds lie above and below the equatorial plane and make an angle of $90^{\circ}$ with the plane. These bonds are called axial bonds

As the axial bond pairs suffer more repulsion from the equatorial bond pairs, axial bonds are slightly longer than equatorial bonds.

Question 39: Define hydrogen bond. Is it weaker or stronger than the van der Waals forces?

Solution. A hydrogen bond is defined as an attractive force acting between the hydrogen attached to an electronegative atom of one molecule and an electronegative atom of a different molecule (may be of the same kind).

Due to a difference between electronegativities, the bond pair between hydrogen and the electronegative atom gets drifted far away from the hydrogen atom. As a result hydrogen atom becomes electropositive with respect to the other atom and acquires a positive charge.



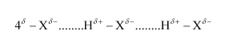
The magnitude of H-bonding is maximum in the solid state and minimum in the gaseous state.

(i) Intermolecular H-bond e.g., $\mathrm{HF}, \mathrm{H}_{2} \mathrm{O}$ etc.

(ii) Intramolecular H-bond e.g., o-nitrophenol



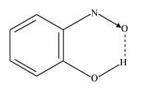
Hydrogen bonds are stronger than Van der Walls forces since hydrogen bonds are regarded as an extreme form of dipole-dipole interaction.

Question 40: What is meant by the term bond order? Calculate the bond order of: $\mathrm{N}_{2}, \mathrm{O}_{2}, \mathrm{O}_{2}^{+}$ and $\mathrm{O}_{2}^{-}$.

Solution. Bond order is defined as one half of the difference between the number of electrons present in the bonding and anti-bonding orbitals of a molecule.

If $N_{\mathrm{a}}$ is equal to the number of electrons in an anti-bonding orbital, then $N_{\mathrm{b}}$ is equal to the number of electrons in a bonding orbital.

Bond order $=\frac{1}{2}\left(N_{\mathrm{b}}-N_{\mathrm{a}}\right)$

If $N_{\mathrm{b}}>N_{\mathrm{a}}$, then the molecule is said be stable. However, if $N_{\mathrm{b}} \leq N_{\mathrm{a}}$, then the molecule is considered to be unstable.

Bond order of $\mathrm{N}_{2}$ can be calculated from its electronic configuration as:



Number of bonding electrons, $N_{\mathrm{b}}=10$

Number of anti-bonding electrons, $N_{\mathrm{a}}=4$

Bond order of nitrogen molecule $=\frac{1}{2}(10-4)$

$=3$

There are 16 electrons in a dioxygen molecule, 8 from each oxygen atom. The electronic configuration of oxygen molecule can be written as:



Since the $1 s$ orbital of each oxygen atom is not involved in boding, the number of bonding electrons $=8=N_{\mathrm{b}}$ and the number of anti-bonding electrons $=4=N_{\mathrm{a}}$

Bond order $=\frac{1}{2}\left(N_{\mathrm{b}}-N_{\mathrm{a}}\right)$

$=\frac{1}{2}(8-4)$

$=2$

Hence, the bond order of oxygen molecule is $2 .$

Similarly, the electronic configuration of $\mathrm{O}_{2}^{+}$ can be written as:



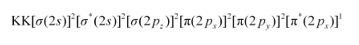
$N_{\mathrm{b}}=8$

$N_{\mathrm{a}}=3$

Bond order of $\mathrm{O}_{2}^{+}=\frac{1}{2}(8-3)$

$=2.5$

Thus, the bond order of $\mathrm{O}_{2}^{+}$ is $2.5$.

The electronic configuration of $\mathrm{O}_{2}^{-}$ ion will be:



$N_{\mathrm{b}}=8$

$N_{\mathrm{a}}=5$

Bond order of $\mathrm{O}_{2}^{-}=\frac{1}{2}(8-5)$

$=1.5$

Thus, the bond order of $\mathrm{O}_{2}^{-}$ ion is $1.5$.

So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.

Also Read,

Download Class 11 Chemistry Notes PDF.

Download Class 11 Chemistry Book Chapterwise PDF.

Download Class 11 Chemistry Exemplar Chapterwise PDF.

If you have any Confusion related to NCERT Solutions for Class 11 Chemistry chapter 4 Chemical Bonding and Molecular Structure PDF then feel free to ask in the comments section down below.

To watch Free Learning Videos on Class 11 Chemistry by Kota’s top IITian’s Faculties Install the eSaral App