
Hey, are you a class 11 student and looking for ways to download NCERT Solutions for Class 11 Chemistry chapter 2 Structure of Atom PDF? If yes. Then read this post till the end.
In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 2 Structure of Atom in PDF that are prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to learn and understand class 11 Chemistry chapter 2 "Structure of Atom" in an easy way then you can use these solutions PDF.
NCERT Solutions helps students to Practice important concepts of subjects easily. Class 11 Chemistry solutions provide detailed explanations of all the NCERT questions that students can use to clear their doubts instantly.
If you want to score high in your class 11 Chemistry Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.
In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 2 Structure of Atom PDF that you can download to start your preparations anytime.
So, without wasting more time Let’s start.
Question 1.Figure the quantity of electrons which will together measure one gram.
(b) Compute the mass and charge of one mole of electrons.
Solution: (a) We know : Mass of an electron $=9.10 \times 10^{-31} \mathrm{~kg}$
$\therefore$ Quantity of electrons that measure $9.10 \times 10^{-31} \mathrm{~kg}=1$
$\therefore$ Quantity of electrons that will measure $1 \mathrm{~g}\left(1 \times 10^{-3} \mathrm{~kg}\right)$
$=\frac{1}{9.1 \times 10^{-31} \mathrm{~kg}} \times\left(1 \times 10^{-3} \mathrm{~kg}\right)$
$=0.109 \times 10^{-3+31}$
$=0.1098 \times 10^{28}$
$=1.098 \times 10^{27}$
(b) (i) We know: Mass of one electron $=9.1 \times 10^{-31} \mathrm{~kg}$
Mass of one mole of electron $=9.1 \times 10^{-31} \mathrm{~kg} \times \mathrm{N}_{\mathrm{A}}=(6.023 \times$
$\left.10^{23}\right) \times\left(9.10 \times 10^{-31} \mathrm{~kg}\right)$
$=5.48 \times 10^{-7} \mathrm{~kg}$
Or
We know Mass of one electron $=9.1 \times 10^{-28} \mathrm{~g}$
The formula used: Mass of one mole of electron
$=$ Mass of one electron $\times \mathrm{N}_{\mathrm{A}}$
$=9.1 \times 10^{-28} \mathrm{~g} \times \mathrm{N}_{\mathrm{A}}$
$=\left(9.1 \times 10^{-28} \mathrm{~g}\right) \times\left(6.023 \times 10^{23}\right)$
$=5.48 \times 10^{-4} \mathrm{~g}$
We know: Charge on one electron $=1.6 \times 10^{-19}$ coulomb
Formula: Charge on one mole of electron $=$ Charge on one electron $\times \mathrm{N}_{\mathrm{A}}$
$=\left(1.6 \times 10^{-19} \mathrm{C}\right) \times \mathrm{N}_{\mathrm{A}}$
$=\left(1.6 \times 10^{-19} \mathrm{C}\right) \times\left(6.023 \times 10^{23}\right)$
$=9.65 \times 10^{4} \mathrm{C}$
Question 2. (I) Calculate the total number of electrons present in one mole of methane.
(II) Find (a) the total number and (b) the total mass of neutrons in $7 \mathrm{mg}$ of $14 \mathrm{c}$.
(Assume that mass of a neutron $=1.67 \times 10^{-27} \mathrm{~kg}$ ).
(III) Find (a) the total number and (b) the total mass of protons in $34 \mathrm{mg}$ of $\mathrm{NH}_{3}$ at STP.
Will the answer change if the temperature and pressure are changed?
Solution: (I) We know : the atomic number of carbon $=6$
The atomic number of hydrogen $=1$
Number of electrons present in 1 molecule of methane $\left(\mathrm{CH}_{4}\right)$
$1(6)+4(1)=10$
Formula used: Number of electrons present in 1 mole of methane
$=$ Number of electrons present in 1 molecule of methane $\times\left(N_{A}\right)$
By putting the above values the formula
$=$ Number of electrons present in 1 molecule of methane $\times 6.023 \times$ $10^{23}$
$=10 \times 6.023 \times 10^{23}=6.023 \times 10^{24}$
(II)
(a) Number of atoms of $14_{C}$ in 1 mole $=6.023 \times 10^{23}$
Since 1 atom of $14_{c}$ contains
Neutrons $=(14-6)=8$
The number of neutrons in $14 \mathrm{~g}$ of $14_{\mathrm{C}}=N_{\mathrm{A}} \times 8=6.023 \times 10^{23} \times 8$
Or, $14 \mathrm{~g}$ of $14_{\mathrm{C}}$ contains $\left(6.023 \times 10^{23} \times 8\right)$ neutrons.
Number of neutrons in $7 \mathrm{mg}\left(7 \times 10^{-3} \mathrm{gram}\right)$
$=\frac{6.023 \times 10^{23} \times 8 \times 7 \times 10^{-3}}{14}$
$=2.40 \times 10^{21}$
(b) (x) The mass of one neutron $=1.67 \times 10^{-24} \mathrm{~g}$
The mass of total neutrons in $7 \mathrm{~g}$ of $14_{\mathrm{C}}$
$=\left(2.4092 \times 10^{21}\right) \times\left(1.67 \times 10^{-24} \mathrm{~g}\right)$
$=4.02 \times 10^{-3} \mathrm{~g}$
(y) The mass of one neutron $=1.67 \times 10^{-27} \mathrm{~kg}$
The mass of total neutrons in $7 \mathrm{~g}$ of $14 \mathrm{c}$
$=\left(2.4092 \times 10^{21}\right)\left(1.67 \times 10^{-27} \mathrm{~kg}\right)$
$=4.0352 \times 10^{-6} \mathrm{~kg}$
(III)
(a) We know: 1 mole of $\mathrm{NH}_{3}=1(14)+3(1) \mathrm{g}$ of $\mathrm{NH}_{3}$
$=17 \mathrm{~g}$ of $\mathrm{NH}_{3}$
$=6.023 \times 10^{23}$ Molecules of $\mathrm{NH}_{3}$
Total number of protons present in 1 molecule of $\mathrm{NH}_{3}$
$=1(7)+3(1)$
$=10$
Number of protons in $6.023 \times 10^{23}$ molecules of $\mathrm{NH}_{3}$
$=\left(6.023 \times 10^{23}\right)(10)$
$=6.023 \times 10^{24}$
$\Rightarrow 17 \mathrm{~g}$ of $\mathrm{NH}_{3}$
Number of protons in $34 \times 10^{-3} \mathrm{~g}$ of $\mathrm{NH}_{3}$
$=\frac{6.023 \times 10^{24} \times 34 \times 10^{-3}}{17}$
$=1.2046 \times 10^{22}$ Protons
(b)(x) We know: Mass of one proton $=1.67 \times 10^{-24} \mathrm{~g}$
The total mass of protons in $34 \mathrm{mg}\left(34 \times 10^{-3} \mathrm{~g}\right.$ ) of
$\mathrm{NH}_{3}$
$=\frac{\left(1.67 \times 10^{-24} \mathrm{~g}\right) \times 6.023 \times 10^{24} \times 34 \times 10^{-3} g}{17}$
$=\left(1.67 \times 10^{-24} \mathrm{~g}\right)\left(1.2046 \times 10^{22}\right)$
$=2.01 \times 10^{-2} \mathrm{~kg}$
(y) $\quad$ Mass of one proton $=1.67 \times 10^{-27} \mathrm{~kg}$
The total mass of protons in $34 \mathrm{mg}$ of $\mathrm{NH}_{3}$
$=\left(1.67 \times 10^{-27} \mathrm{~kg}\right)\left(1.2046 \times 10^{22}\right)$
$=2.0176 \times 10^{-5} \mathrm{~kg}$
The quantity of protons, electrons, and neutrons in a particle is free of temperature what's more, weight conditions. Subsequently, the acquired qualities will stay unaltered if the temperature and weight are changed.
Question 3. What number of neutrons and protons are there in the following nuclei?
${ }_{6}^{13} \mathrm{C},{ }_{8}^{16} \mathrm{O},{ }_{12}^{24} \mathrm{Mg},{ }_{16}^{56} \mathrm{Fe},{ }_{38}^{88} \mathrm{Sr}$
Solution: A symbolic representation of an atom ${ }_{\mathrm{z}}^{\mathrm{A}} \mathrm{x}$ where $\mathrm{A}$ represents Atomic mass (number of proton and neutron) and $Z$ atomic number(number of proton )
${ }_{6}^{13} \mathrm{C}:$
Given: Atomic mass $(\mathrm{A})=13$
Atomic number $(\mathrm{Z})=$ Number of protons $=6$
Formula:Number of neutrons $=$ (Atomic mass)-(Atomic number)
$=13-6=7$
${ }_{8}^{16} \mathrm{O}:$
Given: Atomic mass $(\mathrm{A})=16$
Atomic number $(\mathrm{Z})=8$
Number of protons $=8$
Formula: Number of neutrons $=$ (Atomic mass)- (Atomic number)
$=16-8=8$
${ }_{12}^{24} \mathrm{Mg}:$
Given: Atomic mass $(\mathrm{A})=24$
Atomic number $(\mathrm{Z})=$ Number of protons $=12$
Formula: Number of neutrons $=$ (Atomic mass) - (Atomic number)
$=24-12=12$
${ }_{16}^{56} \mathrm{Fe}$ :
Given: Atomic mass $(\mathrm{A})=56$
Atomic number $(\mathrm{Z})=$ Number of protons $=26$
Formula: Number of neutrons $=$ (Atomic mass)-(Atomic number)
$=56-26=30$
${ }_{38}^{88} \mathrm{Sr}:$
Given: Atomic $\operatorname{mass}(\mathrm{A})=88$
Atomic number $(\mathrm{Z})=$ Number of protons $=38$
Formula: Number of neutrons $=$ (Atomic mass)-(Atomic number)
$=88-38=50$
Question 4. Compose the total image for the atom with the given nuclear number (Z) and Atomic mass (A)
(I) $\mathrm{Z}=17, \mathrm{~A}=35$
(II) $\mathrm{Z}=92, \mathrm{~A}=233$
(III) $\quad \mathrm{Z}=4, \mathrm{~A}=9$
Solution: Symbolic representation of an atom ${ }_{z}^{\mathrm{A}} \mathrm{x}$
(i) $\quad \mathrm{Z}=17, \mathrm{~A}=35:{ }_{17}^{35} \mathrm{C}$
(ii) $\mathrm{Z}=92, \mathrm{~A}=233:{ }_{92}^{233} \mathrm{U}$
(iii) $\mathrm{Z}=4, \mathrm{~A}=9:{ }_{4}^{9} \mathrm{Be}$
Question 5. Yellow light radiated from a sodium light has a wavelength $(\lambda)$ of $580 \mathrm{~nm}$. Ascertain the frequency ( $v$ ) and wave number $(\bar{v})$ of the yellow light.
Solution: given in question: $\mathrm{c}=$ velocity of light in vacuum $=3 \times 10^{8} \frac{\mathrm{m}}{\mathrm{s}}$
the wavelength of yellow light $(\lambda)=580 \mathrm{~nm}=580 \times 10^{-9} \mathrm{~m} / \mathrm{s}$
the formula used : wavelength $(\lambda)$
$=\frac{\text { velocity of light }(\mathrm{c})}{\text { frequency }(\mathrm{v})}$
From the expression we get,
$v=\frac{c}{\lambda} \quad \ldots \ldots \ldots$. $(1)$
Substituting the values in expression (1):
$v=\frac{3 \times 10^{8}}{580 \times 10^{-9}}=5.17 \times 10^{14} \mathrm{~s}^{-1}$
Thus, the frequency of yellow light emitted from the sodium lamp
$=5.17 \times 10^{14} \mathrm{~s}^{-1}$
The wave number of yellow light $\overline{(v)}=\frac{1}{\text { wavelength }(\lambda)}$
$=\frac{1}{580 \times 10^{-9}}=1.72 \times 10^{6} \mathrm{~m}^{-1}$
Question 6. Find energy of each of the photons which
(I) correspond to light of frequency $3 \times 10^{15} \mathrm{~Hz}$.
(II) Have a wavelength of $0.50$ angstrom.
Solution: (I) Given: light of frequency $=3 \times 10^{15} \mathrm{~Hz}$.
The formula used: Energy (E) of one photon $=$ hy
Where $\mathrm{h}=$ Planck's constant $=6.62 \times 10^{-34} \mathrm{Js}$
$v=$ frequency of light $=3 \times 10^{15} \mathrm{~Hz}$
Substituting the above values in the given formula of Energy:
$\mathrm{E}=\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(3 \times 10^{15} \mathrm{~Hz}\right)$
$\mathrm{E}=1.99 \times 10^{-18} \mathrm{~J}$
(II) Given: wavelength $=0.50$ angstrom
Energy (E) of a photon having wavelength $(\lambda)$ is given by the expression,
Formula: $\mathrm{E}=\mathrm{hv}=\frac{\mathrm{hc}}{\lambda}$
$\mathrm{h}=$ Planck's constant $=6.62 \times 10^{-34} \mathrm{Js}$
$\mathrm{c}=$ velocity of light in vacuum $=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$
we know: 1 angstrom $=10^{-10}$ meter
So $0.50$ angstrom $=0.50 \times 10^{-10}$ meter
Substituting the values in the given expression of Energy :
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{0.50 \times 10^{-10}}=3.97 \times 10^{-15} \mathrm{~J}$
$\therefore \mathrm{E}=3.97 \times 10^{-15} \mathrm{~J}$
Question 7. Calculate the wavelength, frequency and wave number of a light wave whose time period is $2.0 \times 10^{-10} \mathrm{~S}$
Solution: Given: time period of light $=2.0 \times 10^{-10} \mathrm{~s}$
The formula used: Frequency of light $(v)=\frac{1}{\text { time Period }}$
$=\frac{1}{2.0 \times 10^{-10} \mathrm{~s}}$
$=5.0 \times 10^{9} \mathrm{~s}^{-1}$
The formula used : Wavelength of light $(\lambda)$
$=\frac{\text { the velocity of light in a vacuum(c) }}{\text { Frequency of light (v) }}$
Where,
$\mathrm{c}=$ velocity of light in vacuum $=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$
Substituting the value in the given expression of $\lambda$ :
$\lambda=\frac{3 \times 10^{8} \mathrm{~m} / \mathrm{s}}{5.0 \times 10^{9} \mathrm{~s}^{-1}}=6.0 \times 10^{-2} \mathrm{~m}$
Wave number $(\bar{v})$ of light $=\frac{1}{\text { wave length }(\lambda)}$
$=\frac{1}{6.0 \times 10^{-2} m}=1.66 \times 10 \mathrm{~m}^{-1}=$
$16.66 \mathrm{~m}^{-1}$
Question 8. What is the quantity of photons of light with a wavelength of $4000 \mathrm{pm}$ that gives $1 \mathrm{~J}$ of energy?
Solution: Given: wavelength of light $=4000 \mathrm{pm}$
energy $=1 \mathrm{~J}$
Formula: Energy (E) of one photon
$=$ Planck's constant (h) $\times$ frequency of light (v)
frequency of light (v) $=\frac{\text { velocity of light }(c)}{\text { wave length }(\lambda)}$
Energy $\left(\mathrm{E}_{n}\right)$ of ' $n$ ' photons $=n h v \Rightarrow n=\frac{E_{n} \lambda}{h c}$
Where the wavelength of light $(\lambda)=4000 \mathrm{pm}=4000 \times 10^{-12} \mathrm{~m}$
The velocity of light in a vacuum $(\mathrm{c})=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$
Planck's constant $(h)=6.62 \times 10^{-34} \mathrm{Js}$
Substituting the values in the given expression of $\mathrm{n}$ :
$\mathrm{n}=\frac{1 \times\left(4000 \times 10^{-12}\right)}{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}=2.01 \times 10^{16}$
Hence, the number of photons with a wavelength of $4000 \mathrm{pm}$ and energy of $1 \mathrm{~J}$ is $2.01 \times 10^{16}$
Question 9. A photon of wavelength $4 \times 10^{-7} \mathrm{~m}$ strikes on metal surface, the work function of the metal being $2.13 \mathrm{eV}$. Calculate
(I) the energy of the photon (eV),
(II) the kinetic energy of the emission, and
(III) the velocity of the photoelectron $\left(1 \mathrm{eV}=1.6020 \times 10^{-19} \mathrm{~J}\right)$
Solution: Given: wavelength of photon $=4 \times 10^{-7} \mathrm{~m}$
work function of the metal $=2.13 \mathrm{eV}$
The energy of one photon
Formula:(E) $=$ Planck's constant $(\mathrm{h}) \times$ frequencyof light $(v)$
$=\frac{\text { Planck's constant }(\mathrm{h}) \times \text { velocity of light (c) }}{\text { wave length of light }(\lambda)}$
Where Planck's constant $(h)=6.62 \times 10^{-34} \mathrm{Js}$
the velocity of light in a vacuum $(c)=3 \times 10^{8} \mathrm{~m} / \mathrm{s} \lambda=$ the wavelength of a photon $(\lambda)=4 \times 10^{-7} \mathrm{~m} / \mathrm{s}$
Substituting the values in the given expression of $E$ :
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{4 \times 10^{-7}}=4.965 \times 10^{-19} \mathrm{~J}$
$\mathrm{Or}=\left(\frac{4.965 \times 10^{-19}}{1.6020 \times 10^{-19}}\right) \mathrm{eV}=3.10 \mathrm{eV}$
Hence, the energy of the photon is $4.97 \times 10^{-19} \mathrm{~J}$ or $3.1020 \mathrm{eV}$
(II) Formula: The kinetic energy of emission $\mathrm{E}_{\mathrm{k}}=\mathrm{hv}-\mathrm{hv}_{0}$
$=(\mathrm{E}-\mathrm{W}) \mathrm{eV}$
$=(3.1020-2.13) \mathrm{eV}$
$=0.9720 \mathrm{eV}$
Hence, the kinetic energy of emission $\left(h v-h v_{0}\right)=0.97 \mathrm{eV}$
$=0.97 \mathrm{eV} \times 1.6020 \times 10^{-19} \mathrm{~J}$
$=1.55 \times 10^{-19} \mathrm{~J}$
(III) Formula: The velocity of a photoelectron (v) can be calculated by the expression,
$\frac{1}{2} \mathrm{mv}^{2}=\mathrm{hv}-\mathrm{h} v_{0}$
$\Rightarrow v=\sqrt{\frac{2\left(h v-h v_{0}\right)}{m}}$
Where $\left(h v-h v_{0}\right)$ is the kinetic energy of emission in Joules = $1.55 \times 10^{-19} \mathrm{~J}$
$' \mathrm{~m}$ ' is the mass of the photoelectron $=9.10939 \times 10^{-31} \mathrm{~kg}$
Substituting the values in the given expression of $\mathrm{v}$ :
$v=\frac{\sqrt{2 \times 1.55 \times 10^{-19} \mathrm{~J}}}{9.10939 \times 10^{-31} \mathrm{~kg}}$
$=\sqrt{0.3418 \times 10^{12} \mathrm{~m}^{2} \mathrm{~s}^{2}}$
$\Rightarrow \mathrm{v}=5.84 \times 10^{5} \mathrm{~ms}^{-1}$
Hence, the velocity of the photoelectron is $5.84 \times 10^{5} \mathrm{~ms}^{-1}$
Question 10. Electromagnetic radiation of wavelength $242 \mathrm{~nm}$ is just sufficient to ionise the sodium atom. Calculate the ionization energy of sodium in $\mathrm{kJ} \mathrm{mol}^{-1}$.
Solution: Given: wavelength of Electromagnetic radiation $(\lambda)=242 \mathrm{~nm}=242 \times 10^{-9} \mathrm{~m}$
Formula used: Energy of sodium atom $(\mathrm{E})=\frac{\mathrm{N}_{\mathrm{A} \mathrm{hc}}}{\lambda}$
Where, Avogadro's number $\left(\mathrm{N}_{\mathrm{A}}\right)=6.023 \times 10^{23}$
Planck's constant $(h)=6.62 \times 10^{-34} \mathrm{Js}$
the velocity of light in vacuum $(c)=3 \times 10^{8}$ meter $/ \mathrm{sec}$
$\mathrm{E}=\frac{\left(6.023 \times 10^{23}\right)\left(6.62 \times 10^{-34}\right) \mathrm{Js}\left(3 \times 10^{8}\right) \mathrm{ms}^{-1}}{242 \times 10^{-9} \mathrm{~m}}$
$=4.947 \times 10^{5} \mathrm{Jmol}^{-1}$
$=494.7 \times 10^{3} \mathrm{Jmol}^{-1}$
$=494 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}$
Question 11. A 25 -watt bulb discharges monochromatic yellow light of a wavelength of $0.57 \mu \mathrm{m}$. Ascertain the rate of discharge of quanta every second.
Solution: Given:
Power of bulb, $P=25$ Watt $=25 \mathrm{Js}^{-1}$
Wavelength $(\lambda)=0.57 \mu \mathrm{m}=0.57 \times 10^{-6}$ meter
Formula: Energy of one photon, $\mathrm{E}=\mathrm{hv}=\frac{\mathrm{hc}}{\lambda}$
Substituting the values in the given expression of E:
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(0.57 \times 10^{-6}\right)}=34.87 \times 10^{-20} \mathrm{~J}$
Rate of emission of quanta per second
$=\frac{\text { power }}{\text { Energy }}=\frac{25}{34.87 \times 10^{-20}}=7.17 \times 10^{19} \mathrm{~s}^{-1}$
Question 12. Electrons are discharged with zero speed from a metal surface when it is presented to radiation of wavelength $6800 A$. Figure limit recurrence $\left(v_{0}\right)$ and work $\left(\mathrm{W}_{0}\right)$ of the metal.
Solution: Given: Threshold wavelength of radiation $\left(\lambda_{0}\right)=6800 A =6800 \times$ $10^{-10} \mathrm{~m}=6.8 \times 10^{-7} \mathrm{~m}$
Formula: Threshold frequency $\left(v_{0}\right)$ of the metal $=\frac{c}{\lambda_{0}}$
$=\frac{3 \times 10^{8} \mathrm{~ms}^{-1}}{6.8 \times 10^{-7} \mathrm{~m}}=4.41 \times 10^{14} \mathrm{~s}^{-1}$
Thus, the threshold frequency $\left(v_{0}\right)$ of the metal $=\mathrm{hv}_{0}$
$=\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(4.41 \times 10^{14} \mathrm{~s}^{-1}\right)$
$=2.922 \times 10^{-19} \mathrm{~J}$
Question 13. What is the wavelength of light transmitted when the electron in a hydrogen atom experiences move from an energy level with $\mathrm{n}=4$ to an energy level with $\mathrm{n}=2 ?$
Solution: Formula: The $n_{i}=4$ to $n_{f}=2$ transition will give rise to a spectral line of the Balmer series. The energy involved in the transition is given by the relation,
$\mathrm{E}=2.18 \times 10^{-18}\left[\frac{1}{\mathrm{n}_{\mathrm{i}}^{2}}-\frac{1}{\mathrm{n}_{\mathrm{f}}^{2}}\right] \mathrm{J}$
Substituting the values in the given expression of $E$ :
$\mathrm{E}=2.18 \times 10^{-18}\left[\frac{1}{4^{2}}-\frac{1}{2^{2}}\right] J$
$\mathrm{E}=2.18 \times 10^{-18}\left[\frac{1}{16}-\frac{1}{4}\right] J$
$=2.18 \times 10^{-18}\left[\frac{1-4}{16}\right] \mathrm{J}$
$=2.18 \times 10^{-18} \times\left(-\frac{3}{16}\right) \mathrm{J}$
$\mathrm{E}=-\left(4.09 \times 10^{-19} \mathrm{~J}\right)$
The negative sign indicates the energy of emission.
formula used: $E=\frac{h c}{\text { wave length }(\lambda)}$
$\therefore$ Wavelength of light emitted $(\lambda)=\frac{\mathrm{hc}}{\mathrm{E}}$
Where, Avogadro's number $\left(\mathrm{N}_{\mathrm{A}}\right)=6.023 \times 10^{23}$
Planck's constant $(h)=6.62 \times 10^{-34} \mathrm{Js}$
the velocity of light in vacuum $(c)=3 \times 10^{8}$ meter $/ \mathrm{sec}$
Substituting the values given above in the formula of Wavelength of light emitted
$\lambda=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(4.0875 \times 10^{-19}\right)}$
$=4.8631 \times 10^{-7} \mathrm{~m}$
$\lambda=486.31 \times 10^{-9} \mathrm{~m} \quad\left(\therefore 10^{-9} \mathrm{~m}=1 \mathrm{~nm}\right)$
$=486 \mathrm{~nm}$
Question 14. What amount of energy is required to ionize a H molecule if the electron involves $\mathrm{n}=5$ circle? Contrast your answer and the ionization enthalpy of $\mathrm{H}$ molecule (energy required to evacuate the electron from $\mathrm{n}=1$ circle).
Solution: Given: principle quantum number $=5$
atomic number of $\mathrm{H}=1$
Formula: The expression of energy is given by,
$\mathrm{E}_{\mathrm{n}}=-\frac{(13.6) \mathrm{Z}^{2}}{\mathrm{n}^{2}} \mathrm{eV}$
$\left(\therefore 1 \mathrm{eV} \times 1.6 \times 10^{-19}=1 \mathrm{~J}\right)$
$=-\frac{\left(2.18 \times 10^{-18}\right) \mathrm{z}^{2}}{\mathrm{n}^{2}} \mathrm{~J}$
Where,
$\mathrm{Z}=$ atomic number of the atom $\mathrm{n}$
$\mathrm{n}=$ principal quantum number
For ionization from $\mathrm{n}_{1}=5$ to $\mathrm{n}_{2}=\infty$,
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{5}$
$=\left[\left(\frac{-(13.6)(1)^{2}}{(\infty)^{2}}\right)-\left(\frac{-(13.6)(1)^{2}}{(5)^{2}}\right)\right] \mathrm{eV}$
$=0.544 \mathrm{eV}$
$\left(\therefore 1 e v \times 1.6 \times 10^{-19}=1 \mathrm{~J}\right)$
$=0.544 \mathrm{eV} \times 1.6 \times 10^{-19} \mathrm{~J}$
$=0.08704 \times 10^{-18} \mathrm{~J}$
$\Delta \mathrm{E}=8.70 \times 10^{-20} \mathrm{~J}$
Hence, the energy required for ionization from $\mathrm{n}=5$ to $\mathrm{n}=\infty$ is
$\Delta \mathrm{E}=8.70 \times 10^{-20} \mathrm{~J}$
Energy required for $\mathrm{n}_{1}=1$ to $\mathrm{n}_{2}=\infty$,
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{5}$
$=\left[\left(\frac{-13.6(1)^{2}}{(\infty)^{2}}\right)-\left(\frac{-13.6(1)^{2}}{(1)^{2}}\right)\right] \mathrm{eV}$
$=13.6 \mathrm{eV}$
$\left(\therefore 1 \mathrm{eV} \times 1.6 \times 10^{-19}=1 \mathrm{~J}\right)$
$=13.6 \mathrm{eV} \times 1.6 \times 10^{-19} \mathrm{~J}$
$=2.18 \times 10^{-18} \mathrm{~J}$
$\Delta \mathrm{E}=2.18 \times 10^{-18} \mathrm{~J}$
Hence, less energy is required to ionize an electron in the $5^{t h}$ orbital of the hydrogen atom as compared to that in the ground state.
Question 15. When the excited electron of an $\mathrm{H}$ atom in $\mathrm{n}=6$ drops to the ground state, the following transitions are possible:
Solution: Hence, the total number of $(5+4+3+2+1) 15$ lines will be obtained in the emission spectrum.
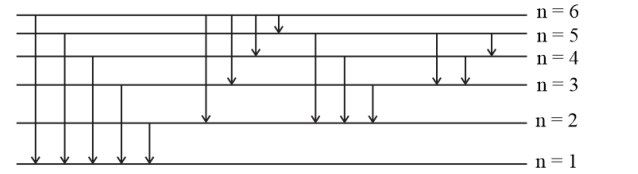
Alternative method:
Formula : The number of spectral lines produced when an electron in the $n^{t h}$ leVel drops down to the ground state
$\frac{n(n-1)}{2}$
Given, $n=6$
Number of spectral lines $=\frac{6(6-1)}{2}=15$
Question 16. (I) Energy associated with the fifth orbit of a hydrogen atom is calculated as:
Solution: Given: hydrogen orbit $(\mathrm{n})=5$
for hydrogen atomic number $(\mathrm{Z})=1$
$\mathrm{E}_{5}=\frac{-(13.6)(\mathrm{Z})^{2}}{(\mathrm{n})^{2}} \mathrm{eV}$
$=\frac{-(13.6)}{(5)^{2}} \mathrm{eV}$
$=\frac{-(13.6)}{25} \mathrm{eV}$
$=2.72 \mathrm{eV}$
$\left(\therefore 1 \mathrm{eV} \times 1.6 \times 10^{-19}=1 \mathrm{~J}\right)$
$=2.72 \mathrm{eV} \times 1.6 \times 10^{-19} \mathrm{~J}$
$=-8.72 \times 10^{-20} \mathrm{~J}$
(II) The radius of Bohr's $n^{t h}$ orbit for atom $\left(\mathrm{r}_{\mathrm{n}}\right)=\frac{(0.0529) \mathrm{n}^{2}}{z} \mathrm{~nm}$
Solution: We know: Hydrogen atom $\mathrm{Z}=1$
Radius For $\mathrm{n}=5$
$\mathrm{r}_{\mathrm{s}}=\frac{(0.0529) \mathrm{n}^{2}}{z}$
$r_{5}=(0.0529) \times(5)^{2} \mathrm{~nm}$
$\mathrm{r}_{5}=(0.0529) \times(25) \mathrm{nm}$
$\mathrm{r}_{5}=1.3225 \mathrm{~nm} \cong 1.32 \mathrm{~nm}$
Question 17. Calculate the wave number for the longest wavelength transition in the Balmer series of atomic hydrogen.
Solution: For the Balmer series, $n_{1}=2$. Thus, the expression of wavenumber $(\bar{v})$ is given by,
$\bar{v}=\left[\frac{1}{(2)^{2}}-\frac{1}{\mathrm{n}_{\mathrm{f}}^{2}}\right]\left(1.097 \times 10^{7} \mathrm{~m}^{-1}\right)$
Formula: Wave number $(\bar{v}) \propto \frac{1}{\text { wavelength of transition }}$.
Hence, for the longest wavelength transition, Wave number $(\bar{v})$ has to be the smallest.
For $(\bar{v})$ to be minimum, $\mathrm{n}_{2}$ should be minimum.
For the Balmer series, a transition from $\mathrm{n}_{1}=2$ to $\mathrm{n}_{2}=3$ is allowed.
Hence, taking $\mathrm{n}_{2}=3$, we get:
$\bar{v}=\left(1.097 \times 10^{7}\right)\left[\frac{1}{(2)^{2}}-\frac{1}{3^{2}}\right]$
$\bar{v}=\left(1.097 \times 10^{7}\right)\left[\frac{1}{4}-\frac{1}{9}\right]$
$=\left(1.097 \times 10^{7}\right)\left[\frac{9-4}{36}\right]$
$=\left(1.097 \times 10^{7}\right)\left[\frac{5}{36}\right]$
$\bar{v}=1.52 \times 10^{6} \mathrm{~m}^{-1}$
Question 18. What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the light emitted when the electron returns to the ground state?
The ground-state electron energy is $-2.18 \times 10^{-11}$ ergs.
Solution: Energy (E) of the $\mathrm{n}^{\text {th }}$ Bohr orbit of an atom is given by
$\mathrm{E}_{5}=\frac{-\left(2.18 \times 10^{-18}\right) \mathrm{Z}^{2}}{(\mathrm{n})^{2}}$
Where $\mathrm{Z}=$ atomic number of the atom
Ground state energy $=-2.18 \times 10^{-11}$ ergs
$=-2.18 \times 10^{-11} \times 10^{-7} \mathrm{~J}$
$\left(\therefore 1\right.$ erg $\left.=10^{-7} \mathrm{~J}\right)$
$=-2.18 \times 10^{-18} \mathrm{~J}$
The energy required to shift the electron from $\mathrm{n}=1$ to $\mathrm{n}=5$ is given as:
$\Delta \mathrm{E}=\mathrm{E}_{5}-\mathrm{E}_{1}$
$=\left[\left(\frac{-\left(2.18 \times 10^{-18} \mathrm{~J}\right)(1)^{2}}{(5)^{2}}\right)-\left(\frac{-2.18 \times 10^{-18}}{1}\right)\right]$
$=\left[\left(\frac{-\left(2.18 \times 10^{-18} \mathrm{~J}\right)(1)^{2}}{25}\right)-\left(\frac{-2.18 \times 10^{-18}}{1}\right)\right]$
$=\left(2.18 \times 10^{-18}\right)\left[1-\frac{1}{25}\right]$
$=\left(2.18 \times 10^{-18}\right)\left[\frac{24}{25}\right]$
$=2.09 \times 10^{-18} \mathrm{~J}$
The wavelength of emitted light $(\lambda)=\frac{h c}{E}$
$\lambda=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(2.0928 \times 10^{-18}\right)}$
$\lambda=9.50 \times 10^{-8} \mathrm{~m}$
Question 19. The electron energy in hydrogen atom is given by $\mathrm{E}_{\mathrm{n}}=\frac{-2.18 \times 10^{-18}}{\mathrm{n}^{2}} \mathrm{~J}$ Calculate the energy required to remove an electron completely from the $\mathrm{n}=2$ orbit. What is the longest wavelength of light in $\mathrm{cm}$ that can be used to cause this transition?
Solution: $\mathrm{E}_{\mathrm{n}}=\frac{-\left(2.18 \times 10^{-18}\right)}{(\mathrm{n})^{2}} \mathrm{~J}$
The energy required for ionization from $\mathrm{n}=2$ is given by,
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{2}$
$=\left[\left(\frac{-2.18 \times 10^{-18}}{(\infty)^{2}}\right)-\left(\frac{\left(-2.18 \times 10^{-18}\right)}{(2)^{2}}\right)\right] \mathrm{J}$
$=\left[\frac{2.18 \times 10^{-18}}{4}-0\right] \mathrm{J}$
$\Delta \mathrm{E}=5.45 \times 10^{-19} \mathrm{~J}$
$\lambda=\frac{h c}{\Delta E}$
plank constant $(\mathrm{h})=6.62 \times 10^{-34}$
velocity of light $(\mathrm{c})=3 \times 10^{8}$
Here, $\lambda$ is the longest wavelength causing the transition.
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(0.57 \times 10^{-6}\right)}=34.87 \times 10^{-20} \mathrm{~J}$
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(5.45 \times 10^{-19}\right)}=3.647 \times 10^{-7} \mathrm{~m}$
$=3647 \times 10^{-10}$ meter
$\left(\therefore 10^{-10}\right.$ meter $= 1$Å)
$=3647 Å$
Question20. Calculate the wavelength of an electron moving with a velocity of $2.05 \times$ $10^{7} \mathrm{~ms}^{-1}$
Solution: Given: A mass of the particle $(\mathrm{m})=9.10939 \times 10^{-31} \mathrm{~kg}$
velocity of particle $(\mathrm{v})=2.05 \times 10^{7} \mathrm{~ms}^{-1}$
To find : wavelength of moving the particle $(\lambda)=?$
Formula used : According to de Broglie's equation,
wave length $(\lambda)=\frac{h}{p}=\frac{h}{m v}$
Planck's constant $(\mathrm{h})=\left(6.62 \times 10^{-34}\right) \mathrm{Js}$
Substituting the above values in the expression of $\lambda:$
$\lambda=\frac{\left(6.62 \times 10^{-34}\right) \mathrm{Js}}{\left(9.10939 \times 10^{-31} \mathrm{~kg}\right)\left(2.05 \times 10^{7} \mathrm{~ms}^{-1}\right)}$
$=3.55 \times 10^{-11} \mathrm{~m}$
Question 21. The mass of an electron is $9.1 \times 10^{-31} \mathrm{~kg}$. If its K.E. is $3.0 \times 10^{-25} \mathrm{~J}$, calculate its wavelength.
Solution: Given: The mass of an electron $=9.1 \times 10^{-31} \mathrm{~kg}$
K.E. of electron $=3.0 \times 10^{-25} \mathrm{~J}$
From de Broglie's equation,
wave length $(\lambda)=\frac{\mathrm{h}}{\mathrm{mv}}$
$h=\left(6.62 \times 10^{-34}\right) \mathrm{Js}$
Given, Kinetic energy $(\mathrm{K} . \mathrm{E})$ of the electron $=3.0 \times 10^{-25} \mathrm{~J}$
Since $\mathrm{K} . \mathrm{E} .=\frac{1}{2} \mathrm{~m} v^{2}$
$\therefore \operatorname{Velocity}(\mathrm{v})=\frac{\frac{\sqrt{2 \mathrm{~K} E}}{\mathrm{~m}}}{1}$
$=\sqrt{\frac{2 \times\left(3.0 \times 10^{-25} \mathrm{~J}\right)}{9.10939 \times 10^{-31} \mathrm{~kg}}}$
$=\sqrt{6.5866 \times 10^{4}}$
$\mathrm{v}=811.58 \mathrm{~ms}^{-1}$
Substituting all values in the expression of $\lambda$ :
$\lambda=\frac{\left(6.62 \times 10^{-34}\right) \mathrm{Js}}{\left(9.10939 \times 10^{-31} \mathrm{~kg}\right)\left(811.579 \mathrm{~ms}^{-1}\right)}$
$=8.9544 \times 10^{-7} \mathrm{~m} \cong 8.95 \times 10^{-7} \mathrm{~m}$
Question 22. (I) Write the electronic configurations of the following ions:
(a) $\mathrm{H}^{-}$
(b) $\mathrm{Na}^{+}$
(c) $\mathrm{O}_{2}^{-}$
(d) $\mathrm{F}^{-}$
(II) What are the atomic numbers of elements whose outermost electrons are represented by
(a) $3 \mathrm{~s}^{1}$
(b) $2 \mathrm{p}^{3}$ and
(c) $3 \mathrm{p}^{5}$
(III) Which atoms are indicated by the following configurations?
(a) [He] $2 \mathrm{~s}^{1}$
(b) $[\mathrm{Ne}] 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}$
(c) $\quad[\mathrm{Ar}] 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}$
Solution: (I) (a) $\mathrm{H}^{-}$ ion :
The atomic number of $\mathrm{H}$ - atom is
The electronic configuration of the $\mathrm{H}$ atom is $1 \mathrm{~s}^{1}$.
A negative charge on the species indicates the addition of an electron by it.
$\therefore$ Electronic configuration of $\mathrm{H}^{-}=1 \mathrm{~s}^{2}$
(b) $\mathrm{Na}^{+}$ ion :
The atomic number of Na-atom is 11
The electronic configuration of the Na atom is $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{1}$.
A positive charge on the species indicates the loss of an electron by it.
$\therefore$ Electronic configuration of $\mathrm{Na}^{+}=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{0}$ or
$1 s^{2} 2 s^{2} 2 p^{6}$
(c) $\mathrm{O}^{2-}$ ion:
The atomic number of $\mathrm{O}-$ atom is 8
The electronic configuration of $\mathrm{O}$ atom is $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{4}$.
A dinegative charge on the species indicates that two electrons are gained by it. $\therefore$ Electronic configuration of $0^{2-}$ ion $=1 s^{2} 2 s^{2} 2 p^{6}$
(d) $\mathrm{F}^{-}$ ion:
The atomic number of $\mathrm{F}$ - atom is 9
The electronic configuration of the $\mathrm{F}$ atom is $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{5}$.
A negative charge on the species indicates the gain of an electron by it.
$\therefore$ Electron configuration of $\mathrm{F}^{-}$ ion $=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6}$
(II) the electron configuration of the element as $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{6} 3 \mathrm{~d}^{6} 4 \mathrm{~s}^{2} \ldots \ldots$
(a) for $3 \mathrm{~s}^{1}$ the inner orbital 1 s2s $2 \mathrm{p}$ should be fulfilled
So the electron configuration of the element $=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{1}$
Number of electrons present in the atom of the element $=2+2+$ $6+1=11$
$\therefore$ The atomic number of the element $=11$
(b) for $2 \mathrm{p}^{3}$ the inner orbital $1 \mathrm{~s} 2 \mathrm{~s}$ should be fulfilled
Completing the electron configuration of the element as $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{3}$
Number of electrons present in the atom of the element $=2+2+$ $3=7$
$\therefore$ The atomic number of the element $=7$
(c) $2 \mathrm{p}^{5}$ the inner orbital $1 \mathrm{~s}, 2 \mathrm{~s}$ should be fulfilled
Completing the electron configuration of the element as $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{5}$
Number of electrons present in the atom of the element $=2+2+$ $5=9$
$\therefore$ Atomic number of the element $=9$
(III) (a) $[\mathrm{He}] 2 \mathrm{~s}^{1}$
The electronic configuration of the element $[\mathrm{He}]=1 \mathrm{~s}^{2}$
The electronic configuration of the element is $[\mathrm{He}] 2 \mathrm{~s}^{1}=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{1}$.
$\therefore$ Atomic number of the element $=3$
Hence, the element with the electronic configuration $[\mathrm{He}] 2 \mathrm{~s}^{1}$ is lithium (Li).
(b) $[\mathrm{Ne}] 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}$
The electronic configuration of the element
$[\mathrm{Ne}] 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6}$
The electronic configuration of the element is $[\mathrm{Ne}]=$ $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}$
$\therefore$ Atomic number of the element $=15$
Hence, the element with the electronic configuration $[\mathrm{Ne}] 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}$ is phosphorus (P).
(c) $[\mathrm{Ar}] 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}$
The electronic configuration of the element
$[\mathrm{Ar}]=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{6}$
The electronic configuration of the element is $[\mathrm{Ar}] 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}=$ $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{6} 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}$
$\therefore$ Atomic number of the element $=21$
Hence, the element with the electronic configuration $[\mathrm{Ar}] 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}$ is scandium $(\mathrm{Sc})$.
Question 23. What is the most reduced estimation of $n$ that permits $g$ orbitals to exist?
Solution: For g-orbitals, $l=4$.
Azimuthal quantum number (l) value $=0$ to $(\mathrm{n}-1)$
"n" of principal quantum number,
$\therefore$ For $\mathrm{l}=4$, least value of $\mathrm{n}=5$
Question 24. An electron is in one of the $3 \mathrm{~d}$ orbitals. Give the possible values of $\mathrm{n}, \mathrm{l}$ and $\mathrm{ml}$ for this electron.
Solution: For the $3 \mathrm{~d}$ orbital:
Principal quantum number $(\mathrm{n})=3$
Azimuthal quantum number (l) $=(\mathrm{n}-1)=3-1=2$
Magnetic quantum number $\left(\mathrm{m}_{1}\right)=+\mathrm{l}$ to $-\mathrm{l}=-2,-1,0,1,2$
Question 25. An atom of an element contains 29 electrons and 35 neutrons. Deduce
(i) The number of protons and
(ii) The electronic configuration of the element.
Solution: (i) For an atom to be neutral, the number of protons is equal to the number of electrons.
$\therefore$ Number of protons in the atom of the given element $=29$
(ii) Number of protons in the atom of the given element $=29$
So The electronic configuration of the atom is $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{6} 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{10}$.
Question 26. Give the number of electrons in the species, $\mathrm{H}_{2}^{+}$ and $\mathrm{H}_{2}$ and $\mathrm{O}_{2}^{+}$
Solution: Atomic number of $\mathrm{H}$ -atom $=1$
In hydrogen atom : Number of proton $=$ Number of electrons $=1$
Number of electrons present in hydrogen molecule $\left(H_{2}\right)=1+1=2$
$\mathrm{H}_{2} \rightarrow \mathrm{H}_{2}^{+}+e^{-}$
$\therefore$ Number of electrons in $\left(\mathrm{H}_{2}^{+}\right)$ molecule $=2-1=1$
$\mathrm{O}_{2}^{+}:$ Atomic number of $\mathrm{O}$ -atom $=8$
In hydrogen atom : Number of proton $=$ Number of electrons $=8$
Number of electrons present in oxygen molecule $\left(\mathrm{O}_{2}\right)=8+8=16$
$\mathrm{O}_{2} \rightarrow \mathrm{O}_{2}^{+}+e^{-}$
$\therefore$ Number of electrons in $\mathrm{O}_{2}^{+}=16-1=15$
Question 27. (I) An atomic orbital has $\mathrm{n}=3$. What are the possible values of $\mathrm{l}$ and $\mathrm{m}_{1}$ ?
(II) List the quantum numbers $\left(\mathrm{m}_{1}\right.$ and $\mathrm{l}$ ) of electrons for $3 \mathrm{~d}$ orbital.
(iii) Which of the following orbitals are possible? $1 \mathrm{p}, 2 \mathrm{~s}, 2 \mathrm{p}$ and $3 \mathrm{f}$
Solution: (I) $\quad \mathrm{n}=3$ (Given)
For a given value of $\mathrm{n}, \mathrm{l}$ can have values from 0 to $(\mathrm{n}-1)$.
$\therefore$ For $\mathrm{n}=3$
l value $=0$ to $(\mathrm{n}-1)=0,1,2$
For a given value of $1, \mathrm{ml}$ can have $(2 \mathrm{l}+1)$ values.
for $1=0$ value, $m_{0}=(2 l+1)=(2 x 0=1)$
$=1$ value $=$ so $\mathrm{m}=0$
for $\mathrm{l}=1$ value, $\mathrm{m}_{1}=(2 \mathrm{l}+1)=(2 \mathrm{x} 1=1)$
$=3$ value $=$ so $\mathrm{m}=-1,0,1$
for $1=2$ value, $m_{2}=(2 l+1)=(2 x 2=1)=5$ value
so, $\mathrm{m}=-2,-1,0,1,2$
(II) For 3 d orbital,
1 value $=0$ to $(\mathrm{n}-1)$
$\mathrm{n}=3$ so $\mathrm{l}=2$
For a given value of $1, \mathrm{~m}$ value $=(2 \mathrm{l}+1)=(2 \mathrm{x} 2+1)=5$
For $\mathrm{l}=2, \mathrm{~m}=-2,-1,0,1,2$
(III) Among the given orbitals only $2 \mathrm{~s}$ and $2 \mathrm{p}$ are possible. $1 \mathrm{p}$ and $3 \mathrm{f}$ cannot exist. For $p$ -orbital, $l=1$.
For a given value of $n, l$ can have values from 0 to $(\mathrm{n}-1)$.
For $\mathrm{l}=1$, the minimum value of $\mathrm{n}=2$
Similarly,
For f-orbital, $\mathrm{l}=4$
For $\mathrm{l}=4$, the minimum value of $\mathrm{n}=5$
$\mathrm{P}$ orbital should be started with $\mathrm{n}=2$ and $\mathrm{f}$ orbital should be started with $\mathrm{n}=5$ Hence, $1 \mathrm{p}$ and $3 \mathrm{f}$ do not exist.
Question 28. Using s, p, d notations, describe the orbital with the following quantum numbers.
(a) $\mathrm{n}=1, \mathrm{l}=0$
(b) $\quad \mathrm{n}=3 ; 1=1$;
(c) $\quad \mathrm{n}=4 ; \mathrm{l}=2$;
(d) $\quad \mathrm{n}=4 ; 1=3$;
Solution: (a) $\mathrm{n}=1, \mathrm{l}=0$ is for s orbital hence The orbital is $1 \mathrm{~s}$.
(b) For $\mathrm{n}=3$ and $\mathrm{l}=1$ for $\mathrm{p}$ orbital hence The orbital is $3 \mathrm{p}$.
(c) For $\mathrm{n}=4$ and $\mathrm{l}=2$ for $\mathrm{d}$ orbital hence The orbital is $4 \mathrm{~d}$.
(d) For $\mathrm{n}=4$ and $\mathrm{l}=3$ for $\mathrm{f}$ orbital hence The orbital is $4 \mathrm{f}$.
Question 29. Explain, giving reasons, which of the following sets of quantum numbers are not possible.
(a) $\mathrm{n}=0, \mathrm{l}=0, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
(b) $\quad \mathrm{n}=1, \mathrm{l}=0, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2}$
(c) $\quad \mathrm{n}=1, \mathrm{l}=1, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
(d) $\mathrm{n}=2, \mathrm{l}=0, \mathrm{~m}_{1}=1, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2}$
(e) $\quad \mathrm{n}=3, \mathrm{l}=3, \mathrm{~m}_{1}=-3, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
(f) $\quad \mathrm{n}=3, \mathrm{l}=0, \mathrm{~m}_{1}=1, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
Solution: (a) $\mathrm{n}=0, \mathrm{l}=0, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
The given set of quantum numbers is not possible because the value of the principal quantum number (n) cannot be zero. $\mathrm{n}=$
$1,1=0, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2} ;$ it is 1s orbital
The given set of quantum numbers is possible.
(b) $\mathrm{n}=1,1=1, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
For the principal quantum number (n) the value of $1=(\mathrm{n}-1)=(1-1)=0$
The given set of quantum numbers is not possible because of the value of the
azimuthal quantum number (l) cannot be equal to the principal quantum number (n)
(d) $\mathrm{n}=2, \mathrm{l}=0, \mathrm{~m}_{1}=1, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2}$
$\mathrm{n}=2, \mathrm{l}=0$ to $(\mathrm{n}-1)$ i.e. 0,1, value of $\mathrm{m}$
$=(1-1): \mathrm{m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2} \mathrm{The}$
given set of quantum numbers is not possible because the value of $\mathrm{m}$ cannot be 1
(e) $\mathrm{n}=3, \mathrm{l}=3, \mathrm{~m}_{1}=-3, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
The given set of quantum numbers is possible. The given set of quantum numbers is not possible. For $n=3, l=0$ to $(3-1) l=0$ to 2 i.e., $0,1,2$
(f) $\mathrm{n}=3,1=0, \mathrm{~m}_{1}=1, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$ The given set of quantum numbers is
possible. because the value of $\mathrm{m}$ cannot be 1
Question 30. How many electrons in an atom may have the following quantum numbers?
(a) $\mathrm{n}=4, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2}$
(b) $\quad \mathrm{n}=3, \mathrm{l}=0$
Solution: (a) Formula: Total number of electrons in an atom for a value of $\mathrm{n}=2 \mathrm{n}^{2}$
$\therefore$ For $\mathrm{n}=4$
Total number of electrons $=2(4)^{2}=32$
The given element has a fully filled orbital as
$1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 4 s^{2} 3 d^{10}$
Hence, all the electrons are paired.
$\therefore$ Number of electrons (having $\mathrm{n}=4$ and $\left.\mathrm{m}_{\mathrm{s}}=-\frac{1}{2}\right)=\frac{32}{2}=16$
(b) $\mathrm{n}=3, \mathrm{l}=0$ indicates that the electrons are present in the $3 \mathrm{~s}$ orbital and $3 \mathrm{~s}$ orbital have only 2 electrons. Therefore, the number of electrons having $\mathrm{n}=3$ and $\mathrm{l}=0$ is 2
Question 31. Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
Solution: Since a hydrogen atom has only one electron, according to Bohr's postulate, the angular momentum of that electron is given by:
Formula: $\mathrm{mvr}=\mathrm{n} \frac{\mathrm{h}}{2 \pi} \ldots .(1)$
Where, $\mathrm{n}=1,2,3, \ldots$
According to de Broglie's equation:
$\lambda=\frac{\mathrm{h}}{\mathrm{mv}} \quad \frac{\mathrm{hr}}{\lambda}=\mathrm{n} \frac{\mathrm{h}}{2 \pi}$
Or
$\mathrm{mv}=\frac{\mathrm{h}}{\lambda} \ldots . .(2)$ or $2 \pi \mathrm{r}=\mathrm{n} \lambda \ldots(3)$
Since ' $2 \pi \mathrm{r}$ ' represents the circumference of the Bohr orbit (r), it is proved by equation (3) that the circumference of the Bohr orbit of the hydrogen atom is an integral multiple of de Broglie's wavelength associated with the electron revolving around the orbit.
Question 32. What transition in the hydrogen spectrum would have the same wavelength as the Balmer transition $\mathrm{n}=4$ to $\mathrm{n}=2$ of $\mathrm{He}^{+}$ spectrum?
Solution: For $\mathrm{He}^{+}$ ion, the wave number associated with the Balmer transition, $\mathrm{n}=4$ to $\mathrm{n}=2$ is given by:
$\bar{v}=\frac{1}{\lambda}=\mathrm{RZ}^{2}\left(\frac{1}{\mathrm{n}_{1}^{2}}-\frac{1}{\mathrm{n}_{2}^{2}}\right)$
Where, $\mathrm{n}_{1}=2 \mathrm{n}_{2}=4$
the atomic number of helium $(\mathrm{Z})=2$
$\bar{v}=\frac{1}{\lambda}=\mathrm{R}(2)^{2}\left(\frac{1}{4}-\frac{1}{16}\right)=4 \mathrm{R}\left(\frac{4-1}{16}\right)$
$\bar{v}=\frac{1}{\lambda}=\frac{3 R}{4}$
$\Rightarrow \lambda=\frac{4}{3 R}$
According to the question, the desired transition for hydrogen will have the same wavelength as that of $\mathrm{He}^{+}$.
$\bar{v}=\mathrm{R}(1)^{2}\left[\frac{1}{\mathrm{n}_{1}^{2}}-\frac{1}{\mathrm{n}_{2}^{2}}\right]=\frac{3 \mathrm{R}}{4}$
$\Rightarrow \mathrm{R}\left[\frac{1}{\mathrm{n}_{1}^{2}}-\frac{1}{\mathrm{n}_{2}^{2}}\right]=\frac{3 \mathrm{R}}{4} \ldots(1)$
By hit and trial method, the equality is given by equation (1) is true only when $\mathrm{n}_{1}=1$ and $\mathrm{n}_{2}=2$
The transition for $\mathrm{n}_{2}=2$ to $\mathrm{n}=1$ in hydrogen spectrum would have the same wavelength as Balmer transition $\mathrm{n}=4$ to $\mathrm{n}=2$ of $\mathrm{He}^{+}$ spectrum.
Question 33. Calculate the energy required for the process
$\mathrm{He}_{(\mathrm{g})}^{+} \rightarrow \mathrm{He}_{(\mathrm{g})}^{2+}+\mathrm{e}^{-}$
The ionization energy for the $\mathrm{H}$ atom in the ground state is $2.18 \times 10^{-18} \mathrm{~J}$ atom $^{-1}$
Solution: Energy associated with hydrogen-like species is given by,
$\mathrm{E}_{\mathrm{n}}=-2.18 \times 10^{-18}\left(\frac{\mathrm{Z}^{2}}{\mathrm{n}^{2}}\right) \mathrm{J}$
For ground state of hydrogen atom,
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{1}$
$=0-\left[-\left(2.18 \times 10^{-18} \frac{(1)^{2}}{(1)^{2}}\right] \mathrm{J}\right.$
$\Delta \mathrm{E}=2.18 \times 10^{-18} \mathrm{~J}$
For the given process,
$\mathrm{He}_{(\mathrm{g})}^{+} \rightarrow \mathrm{He}_{(\mathrm{g})}^{2+}+\mathrm{e}^{-}$
An electron is removed from $\mathrm{n}=1$ to $\mathrm{n}=\infty$.
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{1}$
$=0-\left[-\left(2.18 \times 10^{-18} \frac{(2)^{2}}{(1)^{2}}\right] \mathrm{J}\right.$
$\Delta \mathrm{E}=8.72 \times 10^{-18} \mathrm{~J}$
$\therefore$ The energy required for the process $8.72 \times 10^{-18} \mathrm{~J}$.
Question 34. If the diameter of a carbon atom is $0.15 \mathrm{~nm}$, calculate the number of carbon atoms which can be placed side by side in a straight line across length of scale of length $20 \mathrm{~cm}$ long.
Solution: $1 \mathrm{~m}=100 \mathrm{~cm}$
$1 \mathrm{~cm}=10-2 \mathrm{~m}$
Length of the scale $=20 \mathrm{~cm}$
$=20 \times 10^{-2} \mathrm{~m}$
Diameter of a carbon atom $=0.15 \mathrm{~nm}$
$=0.15 \times 10^{-9} \mathrm{~m}$
One carbon atom occupies $0.15 \times 10^{-9} \mathrm{~m}$.
$\therefore$ Number of carbon atoms that can be placed in a straight line $\frac{20 \times 10^{-2} \mathrm{~m}}{0.15 \times 10^{-9} \mathrm{~m}}$
$=133.33 \times 10^{7}$
$=1.33 \times 10^{9}$
Question 35. $2 \times 10^{8} \mathrm{~m}$ atoms of carbon are arranged side by side. Calculate the radius of carbon atom if the length of this arrangement is $2.4 \mathrm{~cm}$.
Solution: Length of the given arrangement $=2.4 \mathrm{~cm}$
Number of carbon atoms present $=2 \times 10^{8}$
Diameter of carbon atom
$\frac{2.4 \times 10^{-2} \mathrm{~m}}{2 \times 10^{8} \mathrm{~m}} \quad \therefore$ Radius of carbon atom $=1.2 \times 10^{-10} \mathrm{~m}$
$=\frac{\text { Diameter }}{2}$
$=\frac{1.2 \times 10^{-10} \mathrm{~m}}{2}$
$=6.0 \times 10^{-11} \mathrm{~m}$
Question 36. The diameter of zinc atom is 2.6 Å.Calculate
(a) Radius of zinc atom in pm and
(b) Number of atoms present in a length of $1.6 \mathrm{~cm}$ if the zinc atoms are arranged side by side lengthwise.
Solution: (a) Formula: Radius of carbon atom $=\frac{\text { Diameter }}{2}$
$=\frac{2.6}{2}$
$=1.3 \times 10^{-10} \mathrm{~m}$
$=130 \times 10^{-12} \mathrm{~m}$
$=130 \mathrm{pm}$
(b) Length of the arrangement $=1.6 \mathrm{~cm}$
$=1.6 \times 10^{-2} \mathrm{~m}$
Diameter of zinc atom $=1.6 \times 10^{-10} \mathrm{~m}$
$\therefore$ Number of zinc atoms present in the arrangement
$=1 \cdot \frac{6 \times 10^{-2} \mathrm{~m}}{2.6 \times 10^{-10} \mathrm{~m}}$
$=0.6153 \times 10^{8} \mathrm{~m}$
$=6.153 \times 10^{7} \mathrm{~m}$
Question 37. The diameter of zinc atom is 2.6 Å. Calculate
(a) radius of zinc atom in pm and
(b) number of atoms present in a length of $1.6 \mathrm{~cm}$ if the zinc atoms are arranged side by side lengthwise.
Solution: (a) Radius of carbon atom $=\frac{\text { Diameter }}{2}$
$=\frac{2.6}{2}$
$=1.3 \times 10^{-10} \mathrm{~m}$
$=130 \times 10^{-12} \mathrm{~m}$
$=130 \mathrm{pm}$
(b) Length of the arrangement $=1.6 \mathrm{~cm}$
$=1.6 \times 10^{-2} \mathrm{~m}$
Diameter of zinc atom $=1.6 \times 10^{-10} \mathrm{~m}$
Therefore, Number of zinc atoms present in the arrangement
$=\frac{1.6 \times 10^{-2} \mathrm{~m}}{2.6 \times 10^{-10} \mathrm{~m}}$
$=0.6153 \times 10^{8} \mathrm{~m}$
$=6.153 \times 10^{7} \mathrm{~m}$
Question 38. A certain particle carries $2.5 \times 10^{-16} \mathrm{C}$ of static electric charge. Calculate the number of electrons present in it.
Solution: Charge on one electron $=1.6022 \times 10^{-19} \mathrm{C}$
$\Rightarrow 1.6022 \times 10^{-19} \mathrm{C}$ charge is carried by 1 electron.
Therefore, Number of electrons carrying a charge of
$2.5 \times 10^{-16} \mathrm{C} \frac{1}{1.6022 \times 10^{-19} \mathrm{C}}\left(2.5 \times 10^{-16} \mathrm{C}\right)$
$=1.560 \times 10^{3} \mathrm{C}$
$=1560 \mathrm{C}$
Question 39. In Milikan's experiment, static electric charge on the oil drops has been obtained by shining X-rays. If the static electric charge on the oil drop is $-1.282 \times$ $10^{-18} \mathrm{C}$, calculate the number of electrons present on it.
Solution: Charge on the oil drop $=1.282 \times 10^{-18} \mathrm{C}$
Charge on one electron $=1.6022 \times 10^{-19} \mathrm{C}$
Therefore, Number of electrons present on the oil drop
$\frac{1.282 \times 10^{-18} \mathrm{C}}{1.6022 \times 10^{-19} \mathrm{C}}$
$=0.8001 \times 10^{1}$
$=8.0$
Question 40. In Rutherford's experiment, generally the thin foil of heavy atoms, like gold, platinum etc. have been used to be bombarded by the $\alpha$ -particles. If the thin foil of light atoms like Aluminium etc. is used, what difference would be observed from the above results?
Solution: A thin foil of lighter atoms will not give the same results as given with the foil of heavier atoms.
Lighter atoms would be able to carry very little positive charge. Hence, they will not cause enough deflection of $\alpha$ -particles (positively charged).
Question 41. Symbols ${ }_{35}^{79} \mathrm{Br}$ and ${ }^{79} \mathrm{Br}$ can be written, whereas symbols ${ }_{79}^{35} \mathrm{Br}$ and ${ }^{35} \mathrm{Br}$ are not acceptable. Answer briefly.
Solution: The general convention of representing an element along with its atomic mass (A) and atomic number (Z) is ${ }_{\mathrm{Z}}^{\mathrm{A}} \mathrm{X}$.
Hence, ${ }_{35}^{79} \mathrm{Br}$ is acceptable but ${ }_{79}^{35} \mathrm{Br}$ is not acceptable.
${ }^{79} \mathrm{Br}$ can be written but ${ }^{35} \mathrm{Br}$ cannot be written because the atomic number of an element is constant, but the atomic mass of an element depends upon the relative abundance of its isotopes. Hence, it is necessary to mention the atomic mass of an element.
Question 42. An element with mass number 81 contains $31.7 \%$ more neutrons as compared to protons. Assign the atomic symbol.
Solution: Let the number of protons in the element be $\mathrm{x}$.
Therefore, Number of neutrons in the element $=\mathrm{x}+31.7 \%$ of $\mathrm{x}$
$=\mathrm{x}+0.317 \mathrm{x}$
$=1.317 \mathrm{x}$
According to the question,
Mass number of the element $=81$
Therefore, (Number of protons $+$ number of neutrons $)=81$
$\Rightarrow x+1.317 x=81 \simeq 35$
$2.317 x=81 x$
$=\frac{81}{2.317}$
$=34.95 \cong 35$
Hence, the number of protons in the element i.e., $\mathrm{x}$ is 35 .
Since the atomic number of an atom is defined as the number of protons present in its nucleus, the atomic number of the given element is 35 .
Therefore, the atomic symbol of the element is ${ }_{35}^{81} \mathrm{Br}$
Question 43. An ion with mass number 37 possesses one unit of negative charge. If the ion contains $11.1 \%$ more neutrons than the electrons, find the symbol of the ion.
Solution: Let the number of electrons in the ion carrying a negative charge be $\mathrm{x}$.
$=\mathrm{x}+0.111 \mathrm{x}$
$=1.111 \mathrm{x}$
Number of electrons in the neutral atom $=(\mathrm{x}-1)$
(When an ion carries a negative charge, it carries an extra electron)
Therefore, Number of protons in the neutral atom $=\mathrm{x}-1$
Given,
Mass number of the ion $=37$
Therefore, $(\mathrm{x}-1)+1.111 \mathrm{x}=37$
$2.111 x=38 x$
$=18$
Therefore, The symbol of the ion is ${ }_{17}^{37} \mathrm{Cl}^{-}$
Question 44. An ion with mass number 56 contains 3 units of positive charge and $30.4 \%$ more neutrons than electrons. Assign the symbol to this ion.
Solution: Let the number of electrons present in ion $A^{3+}$ be $x$.
Therefore, Number of neutrons in $\mathrm{it}=x+30.4 \%$ of $x=1.304 x$
Since the ion is tripositive,
$\Rightarrow$ Number of electrons in neutral atom $=x+3$
Therefore, Number of protons in neutral atom $=x+3$
Given: Mass number of the ion $=56$
Therefore, $(x+3)(1.304 x)=56$
$2.304 x=53$
$x=532.304$
$x=23$
Therefore, Number of protons $=x+3=23+3=26$
Therefore, The symbol of the ion $\frac{56}{26} \mathrm{Fe}^{+}$
Question 45. Arrange the following type of radiations in increasing order of frequency:
(a) radiation from microwave oven
(b) amber light from traffic signal
(c) radiation from FM radio
(d) cosmic rays from outer space and
(e) X-rays.
Solution: The increasing order of frequency is as follows:
Radiation from FM radio $<$ amber light $<$ radiation from microwave oven $<\mathrm{X}-$ rays $<$ cosmic rays
The increasing order of wavelength is as follows:
Cosmic rays $
Question 46. Nitrogen laser produces a radiation at a wavelength of $337.1 \mathrm{~nm}$. If the number of photons emitted is $5.6 \times 1024$, calculate the power of this laser.
Solution: Power of laser $=$ Energy with which it emits photons
Formula: Power $=\mathrm{E}=$ Nhc $\lambda$
Where, $\mathrm{N}=$ number of photons emitted
$\mathrm{h}=$ Planck's constant
$\mathrm{c}=$ velocity of radiation
$\lambda=$ wavelength of radiation
Substituting the values in the given expression of Energy (E):
$E=\frac{\left(5.6 \times 10^{24}\right)(6.62 \times 10-34 \mathrm{Js})\left(3 \times 10^{8} \mathrm{~ms}-1\right)}{337.1 \times 10^{-9} \mathrm{~m}}$
$=0.3302 \times 10^{7} \mathrm{~J}$
$=3.33 \times 10^{6} \mathrm{~J}$
Hence, the power of the laser is $3.33 \times 10^{6} \mathrm{~J}$
Question 47. Neon gas is generally used in the sign boards. If it emits strongly at $616 \mathrm{~nm}$, calculate
(a) the frequency of emission,
(b) distance traveled by this radiation in $30 \mathrm{~s}$
(c) energy of quantum and
(d) number of quanta present if it produces $2 \mathrm{~J}$ of energy.
Solution: Wavelength of radiation emitted $=616 \mathrm{~nm}=616 \times 10^{-9} \mathrm{~m}$ (Given)
(a) Frequency of emission (v)
$v=c \lambda$
Where, $\mathrm{c}=$ velocity of radiation
$\lambda=$ wavelength of radiation
Substituting the values in the given expression of $(v)$ :
$v=3 \times \frac{108 \mathrm{~m}}{\mathrm{~s} 616} \times 10^{-9} \mathrm{~m}$
$=4.87 \times 10^{8} \times 10^{9} \times 10^{-3} \mathrm{~s}^{-1}$
$\mathrm{v}=4.87 \times 10^{14} \mathrm{~s}^{-1}$
Frequency of emission $(v)=4.87 \times 10^{14} \mathrm{~s}^{-1}$
(b) We know: Velocity of radiation, $\mathrm{c}=3 \times 10^{8} \mathrm{~ms}^{-1}$
Distance travelled by this radiation in $30 \mathrm{~s}$
$=\left(3 \times 10^{8} \mathrm{~ms}^{-1}\right)(30 \mathrm{~s})$
$=9 \times 10^{9} \mathrm{~m}$
(c) Energy of quantum $(\mathrm{E})=\mathrm{h} v$
$=\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(4.87 \times 10^{14} \mathrm{~s}^{-1}\right)$
Energy of quantum $(\mathrm{E})=32.27 \times 10^{-20} \mathrm{~J}$
Therefore, $32.27 \times 10^{-20} \mathrm{~J}$ of energy is present in 1 quantum.
Number of quanta in $2 \mathrm{~J}$ of energy
$\frac{2 \mathrm{~J}}{32.27 \times 10^{-20} \mathrm{~J}}=6.19 \times 10^{18}=6.2 \times 10^{18}$
Question 48. In astronomical observations, signals observed from the distant stars are generally weak. If the photon detector receives a total of $3.15 \times 10^{-18} \mathrm{~J}$ from the radiations of $600 \mathrm{~nm}$, calculate the number of photons received by the detector.
Solution: We know: velocity of radiation (c) $=3 \times 10^{8} \mathrm{~ms}^{-1}$
Planck's constant $(\mathrm{h})=6.62 \times 10^{-34} \mathrm{Js}$
Given: Wavelength $(\lambda)=600 \mathrm{~nm}$
Energy received by the photons $=3.15 \times 10^{-18} \mathrm{~J}$
From the expression of energy of one photon (E),
Formula: $\mathrm{E}=$ hc $\lambda$
Where,
$\lambda=$ wavelength of radiation
$\mathrm{h}=$ Planck's constant
$\mathrm{c}=$ velocity of radiation
Substituting the values in the given expression of $\mathrm{E}$ :
$E=\frac{\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(3 \times 10^{8} \mathrm{~ms}^{-1}\right)}{600 \times 10^{-9}}=3.313 \times 10^{-19} \mathrm{~J}$
Energy of one photon $=3.313 \times 10^{-19} \mathrm{~J}$
Number of photons received with $3.15 \times 10^{-18} \mathrm{~J}$ of energy
$=\frac{3.15 \times 10^{-18} \mathrm{~J}}{3.313 \times 10^{-19} \mathrm{~J}}$
$=9.5 \approx 10$
Question 49. Lifetimes of the molecules in the excited states are often measured by using pulsed radiation source of duration nearly in the nano second range. If the radiation source has the duration of $2 \mathrm{~ns}$ and the number of photons emitted during the pulse source is $2.5 \times 10^{15} \mathrm{~J}$, calculate the energy of the source.
Solution: Frequency of radiation (v),
$v=12.0 \times 10^{-9} \mathrm{~s}$
$v=5.0 \times 10^{8} \mathrm{~s}^{-1}$
Energy (e) $\quad$ of source $=\mathrm{Nhv}$
Where,
$\mathrm{N}=$ number of photons emitted
$\mathrm{h}=$ Planck's constant
$v=$ frequency of radiation
Substituting the values in the given expression of (E):
$\mathrm{E}=\left(2.5 \times 10^{15}\right)\left(6.62 \times 10^{-34} \mathrm{Js}\right)(5.0 \times 108 \mathrm{~s}-1)$
$\mathrm{E}=8.282 \times 10^{-10} \mathrm{~J}$
Hence, the energy of the source (e) is $8.282 \times 10^{-10} \mathrm{~J}$.
Question 50. The work function for cesium atom is $1.9 \mathrm{eV}$. Calculate
(a) the threshold wavelength and
(b) the threshold frequency of the radiation. If the cesium element is irradiated with a wavelength $500 \mathrm{~nm}$, calculate the kinetic energy and the velocity of the ejected photoelectron.
Solution: It is given that the work function $\left(\mathrm{W}_{0}\right)$ for cesium atom is $1.9 \mathrm{eV}$.
(a) From the $\mathrm{W}_{0}=\mathrm{hc} \lambda_{0}$ expression, we get:
$\lambda_{0}=\mathrm{hcW}_{0}$
Where,
$\lambda_{0}=$ threshold wavelength
$\mathrm{h}=$ Planck's constant
$c=$ velocity of radiation
Substituting the values in the given expression of $\left(\lambda_{0}\right):$
$\lambda_{0}=\frac{\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(3 \times 10^{8} \mathrm{~ms}^{-1}\right)}{\left(1.9 \times 1.602 \times 10^{-19} \mathrm{~J}\right)}$
$=6.53 \times 10^{-7} \mathrm{~m}$
Hence, the threshold wavelength $\left(\lambda_{0}\right)$ is $653 \mathrm{~nm}$.
(b) Formula: From the expression, $W_{0}=h v_{0}$, we get:
$v_{0}=W_{0} h$
Where,
$v_{0}=$ threshold frequency
$\mathrm{h}=$ Planck's constant
Substituting the values in the given expression of $v_{0}$ :
$v_{0}=\frac{1.9 \times 1.602 \times 10^{-19} \mathrm{~J}}{6.62 \times 10^{-34} \mathrm{Js}}$
(i e., $\left.V=1.602 \times 10^{-19} \mathrm{~J}\right)$
$v_{0}=4.593 \times 10^{14} \mathrm{~s}^{-1}$
Hence, the threshold frequency of radiation $\left(v_{0}\right)$ is $4.593 \times 10^{14} \mathrm{~s}^{-1}$
(c) According to the question:
Wavelength used in irradiation $(\lambda)=500 \mathrm{~nm}$
Formula: Kinetic energy $=\mathrm{h}(v-v 0)$
$=\mathrm{hc}\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)$
$=\left(6.62 \times 10^{-34} \mathrm{Js}\right)(3.0 \times 108 \mathrm{~ms}-1)\left(\frac{\lambda_{0}-\lambda}{\lambda \lambda_{0}}\right)$
$=\left(1.9878 \times 10^{-26} \mathrm{Jm}\right)\left[\frac{(653-500) 10^{-9} \mathrm{~m}}{(653)(500) 10^{-18} \mathrm{~m}^{2}}\right]$
$=\frac{\left(1.9878 \times 10^{-26}\right)\left(153 \times 10^{9}\right)}{(653)(500) \mathrm{J}}=9.3149 \times 10^{-20} \mathrm{~J}$
Kinetic energy of the ejected photoelectron $=9.3149 \times 10^{-20} \mathrm{~J}$
Since K. E = $\frac{1}{2} \mathrm{mv}^{2}=9.3149 \times 10^{-20} \mathrm{~J}$
$v=\sqrt{\frac{2\left(9.3149 \times 10^{-20} \mathrm{~J}\right)}{9.10939 \times 10-31}}$
$=\sqrt{2.0451 \times 10^{11} \mathrm{~m}^{2} \mathrm{~s}^{2}}$
$=4.52 \times 10^{5} \mathrm{~ms}^{-1}$
Question 51. Following results are observed when sodium metal is irradiated with different wavelengths. Calculate
(a) Threshold wavelength and,
(b) Planck's constant.
Solution: (a) Assuming the threshold wavelength to be $\lambda_{0} \mathrm{~nm}\left(=\lambda_{0} \times 10^{-} 9 \mathrm{~m}\right)$, the kinetic energy of the radiation is given as:
$\mathrm{h}\left(v-v_{0}\right)=\frac{1}{2} \mathrm{mv}^{2}$
Three different equalities can be formed by the given value as:
$\mathrm{h}\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)=\frac{1}{2} \mathrm{mv}^{2}$
$h c\left(\frac{1}{500 \times 10^{9}}-\frac{1}{\lambda_{0} \times 10-9 m}\right)$
$=\frac{1}{2} m\left(2.55 \times 10^{+5} \times 10^{-2} \mathrm{~ms}^{-1}\right)$
$\frac{h c}{10^{-9} m}\left(\frac{1}{500}-\frac{1}{\lambda_{0}}\right)=12 m\left(2.55 \times 10^{+3} m s^{-1}\right)^{2}$(1)
Similarly,
$\frac{h c}{10^{-9} m}\left(\frac{1}{450}-\frac{1}{\lambda_{0}}\right)=\frac{1}{2 m}$
$\left(3.45 \times 10^{+3} \mathrm{~ms}^{-1}\right)^{2}$(2)
$\frac{h c}{10^{-9} m}\left(\frac{1}{400}-\frac{1}{\lambda_{0}}\right)=\frac{1}{2 m}$
$\left(5.35 \times 10^{+3} \mathrm{~ms}^{-1}\right)^{2}$(3)
Dividing equation (3) by equation (1):
$\frac{\left[\frac{\lambda_{0}-400}{400 \lambda_{0}}\right]}{\left[\frac{\lambda_{0}-500}{500 \lambda_{0}}\right]}=\frac{\left(5.35 \mid \times 10^{+3} \mathrm{~ms}^{-1}\right)^{2}}{\left(2.55 \mid \times 10^{+3} \mathrm{~ms}^{-1}\right)^{2}}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=\frac{(5.35)^{2}}{(2.55)^{2}}=\frac{28.6225}{6.5025}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=4.40177$
$17.6070 \lambda_{0}-5 \lambda_{0}=8803.537-2000$
$\lambda_{0}=\frac{6805.537}{12.607}$
$\lambda_{0}=539.8 \mathrm{~nm}$
$\lambda_{0}=540 \mathrm{~nm}$
So, threshold wavelength $\left(\lambda_{0}\right)=540 \mathrm{~nm}$
(b) of the question is not done due to the incorrect values of velocity given in the question.
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=(5.35)^{2}(2.55)^{2}$
$=\frac{28.6225}{6.5025}$
$\frac{5 \lambda_{0}-2000}{4 \lambda 0-2000}=4.40177$
$17.6070 \lambda_{0}-5 \lambda_{0}=8803.537-2000$
$\lambda_{0}=\frac{6805.537}{12.607}$
$\lambda_{0}=539.8 \mathrm{~nm}$
$\lambda_{0}=540$
Question 52. The ejection of the photoelectron from the silver metal in the photoelectric effect experiment can be stopped by applying the voltage of $0.35 \mathrm{~V}$ when the radiation $256.7 \mathrm{~nm}$ is used. Calculate the work function for silver metal.
Solution: Given: Stopping potential $=0.35 \mathrm{~V}$
Wavelength of radiation $=256.7 \mathrm{~nm}$
We know: velocity of radiation $(\mathrm{c})=3 \times 10^{8} \mathrm{~ms}^{-1}$
Planck's constant $(\mathrm{h})=6.62 \times 10^{-34} \mathrm{Js}$
From the principle of conservation of energy, the energy of an incident photon (e) is equal to the sum of the work function $\left(\mathrm{W}_{0}\right)$ of radiation and its kinetic energy (K.E) i.e.,
Fomula: $E=W_{0}+K . E$
$\Rightarrow \mathrm{W}_{0}=\mathrm{E}-\mathrm{K} . \mathrm{E}$
Formula: Energy of incident photon $(\mathrm{E})=\frac{\mathrm{hc}}{\lambda}$
Where,
$\mathrm{c}=$ velocity of radiation
$\mathrm{h}=$ Planck's constant
$\lambda=$ wavelength of radiation
Substituting the values in the given expression of $E$ :
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(3 \times 10^{8} \mathrm{~ms}^{-1}\right)}{\left(256.7 \times 10^{-9} \mathrm{~m}\right)}$
$=7.744 \times 10^{-19} \mathrm{~J}$
$=\frac{7.744 \times 10^{-19}}{1.602 \times 10^{-19}} \mathrm{eV}$
$\mathrm{E}=4.83 \mathrm{eV}$
The potential applied to silver metal changes to kinetic energy (K.E) of the photoelectron.
Hence,
$\mathrm{K} . \mathrm{E}=0.35 \mathrm{~V}$
$\mathrm{K} . \mathrm{E}=0.35 \mathrm{eV}$
Therefore, Work function, $\mathrm{W}_{0}=\mathrm{E}-\mathrm{K} . \mathrm{E} \quad[$ Formula $]$
$=4.83 \mathrm{eV}-0.35 \mathrm{eV}$
$=4.48 \mathrm{eV}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=\frac{(5.35)^{2}}{(2.55)^{2}}=\frac{28.6225}{6.5025}$
$5 \lambda_{0}-20004 \lambda_{0}-2000=4.40177$
$17.6070 \lambda_{0}-5 \lambda_{0}=8803.537-2000$
$\lambda_{0}=\frac{6805.537}{12.607}$
$\lambda_{0}=539.8 \mathrm{~nm}$
$\lambda_{0} \simeq 540 \mathrm{~nm}$
Question 53. If the photon of the wavelength $150 \mathrm{pm}$ strikes an atom and one of its inner bound electrons is ejected out with a velocity of $1.5 \times 10^{7} \mathrm{~ms}^{-1}$, calculate the energy with which it is bound to the nucleus.
Solution: Given: Wavelength of photon $=150 \mathrm{pm}$
Velocity of ejected electrons $=1.5 \times 10^{7} \mathrm{~ms}^{-1}$
We know: velocity of radiation $(\mathrm{c})=3 \times 10^{8} \mathrm{~ms}^{-1}$
Planck's constant $(\mathrm{h})=6.62 \times 10^{-34} \mathrm{Js}$
Formula: Energy of incident photon (E)is given by,
$\mathrm{E}=\frac{\mathrm{hc}}{\lambda}$
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(150 \times 10^{-12}\right)}$
$=1.3252 \times 10^{-15} \mathrm{~J}$
$\simeq 13.252 \times 10^{-16} \mathrm{~J}$
Energy of the electron ejected $(\mathrm{K} . \mathrm{E})=\frac{1}{2} \mathrm{~m}_{\mathrm{e}} v^{2}$
$=12\left(9.10939 \times 10^{-31} \mathrm{~kg}\right)$
$\left(1.5 \times 10^{7} \mathrm{~ms}^{-1}\right)^{2}$
$=10.2480 \times 10^{-17} \mathrm{~J}$
$=1.025 \times 10^{-16} \mathrm{~J}$
Hence, the energy with which the electron is bound to the nucleus can be obtained as:
$=\mathrm{E}-\mathrm{K} . \mathrm{E}$
$=13.252 \times 10^{-16} \mathrm{~J}-1.025 \times 10^{-16} \mathrm{~J}$
$=12.227 \times 10^{-16} \mathrm{~J}$
$=\frac{12.227 \times 10^{-16}}{1.602 \times 10^{-19}} \mathrm{eV}$
$=7.6 \times 10^{3} \mathrm{eV}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=\frac{(5.35)^{2}}{(2.55)^{2}}=\frac{28.6225}{6.5025}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=4.40177$
$17.6070 \lambda_{0}-5 \lambda_{0}=8803.537-2000$
$\lambda_{0}=\frac{6805.537}{12.607}$
$\lambda_{0}=539.8 \mathrm{~nm}$
$\lambda_{0} \simeq 540 \mathrm{~nm}$
Question 54. Emission transitions in the Paschen series end at orbit $\mathrm{n}=3$ and start from orbit $\mathrm{n}$ and can be represented as $\mathrm{v}=3.29 \times 10^{15} \mathrm{~Hz}\left[\frac{1}{3^{2}}-\frac{1}{\mathrm{n}^{2}}\right]$ Calculate the value of $\mathrm{n}$ if the transition is observed at $1285 \mathrm{~nm}$. Find the region of the spectrum.
Solution: Given: Wavelength of transition $=1285 \mathrm{~nm}$
$=1285 \times 10^{-9} \mathrm{~m}$
$v=3.29 \times 10^{15}\left(\frac{1}{3^{2}}-\frac{1}{n^{2}}\right)$
Formula: Since $v=\frac{c}{\lambda}$
$=\frac{3 \times 10^{8} \mathrm{~ms}^{-1}}{1285 \times 10-9 \mathrm{~m}}$
Now, $v=2.33 \times 10^{14} \mathrm{~s}^{-1}$
Substituting the value of $v$ in the given expression,
$3.29 \times 10^{15}\left(\frac{1}{9}-\frac{1}{\mathrm{n}^{2}}\right)=2.33 \times 10^{14}$
$\frac{1}{9}-\frac{1}{n^{2}}=\frac{2.33 \times 10^{14}}{3.29 \times 10^{15}}$
$\frac{1}{9}-0.7082 \times 10^{-1}=\frac{1}{n^{2}}$
$\Rightarrow \frac{1}{\mathrm{n}^{2}}=1.1 \times 10^{-1}-0.7082 \times 10^{-1}$
$\frac{1}{n^{2}}=4.029 \times 10^{-2} n$
$=14.029 \times 10^{-2}$
$\mathrm{n}=4.98$
$n=5$
Hence, for the transition to be observed at $1285 \mathrm{~nm}, \mathrm{n}=5$. The spectrum lies in the infra-red region.
Question 55. Calculate the wavelength for the emission transition if it starts from the orbit having radius $1.3225 \mathrm{~nm}$ and ends at $211.6 \mathrm{pm}$. Name the series to which this transition belongs and the region of the spectrum.
Solution: Radius of the initial orbit $=1.3225 \mathrm{~nm}$
Radius of the final orbit $=211.6 \mathrm{pm}$
Formula: The radius of the $\mathrm{n}$ th orbit of hydrogen-like particles is given by,
$r=\frac{0.529 n^{2}}{Z} Å$
$\mathrm{r}=\frac{5.29 \mathrm{n}^{2}}{\mathrm{Z}} \mathrm{pm}$
For radius $\left(r_{1}\right)=1.3225 \mathrm{~nm}$
$=1.32225 \times 10^{-9} \mathrm{~m} \mathrm{n}_{1}^{2}=\frac{\mathrm{r}_{1} \mathrm{z}}{52.9}$
$=1322.25 \times 10^{-12} \mathrm{~m} \mathrm{n}_{1}^{2}=\frac{1322.25 \mathrm{Z}}{52.9}$
$=1322.25 \mathrm{pm}$
Similarly,
$\mathrm{n}_{2}^{2}=\frac{211.6 \mathrm{Z}}{52.9}$
$\frac{\mathrm{n}_{1}^{2}}{\mathrm{n}_{2}^{2}}=\frac{1322.5}{211.6}$
$\frac{\mathrm{n}_{1}^{2}}{\mathrm{n}_{2}^{2}}=6.25$
$\frac{\mathrm{n}^{1}}{\mathrm{n}^{2}}=2.5$
$\frac{\mathrm{n}^{1}}{\mathrm{n}^{2}}=\frac{25}{10}=\frac{5}{2}$
$\Rightarrow \mathrm{n} 1=5$ and $\mathrm{n} 2=2$ Thus, the transition is from the 5 th orbit to the 2 nd orbit. It belongs to the Balmer series. wave number $(\bar{v})$ for the transition is given by,
$1.097 \times 10^{7}\left(\frac{1}{2^{2}}-\frac{1}{5^{2}}\right) \mathrm{m}^{-1}$
$=1.097 \times 10^{7} \mathrm{~m}^{-1}\left(\frac{21}{100}\right)$
$=2.303 \times 10^{6} \mathrm{~m}^{-1}$
Wavelength $(\lambda)$ associated with the emission transition is given by,
$\lambda=1 v$
$=12.303 \times 10^{6} \mathrm{~m}^{-1}$
$=0.434 \times 10^{-6} \mathrm{~m} \lambda$
$=434 \mathrm{~nm}$
Question 56. Dual behavior of matter proposed by de Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules and other type of material. If the velocity of the electron in this microscope is $1.6 \times 10^{6} \mathrm{~ms}^{-1}$, calculate de Broglie wavelength associated with this electron.
Solution: Given: velocity of the electron $=1.6 \times 10^{6} \mathrm{~ms}^{-1}$
We know: Mass of electron $=9.103939 \times 10^{-31} \mathrm{~kg}$
Formula: From de Broglie's equation,
$\lambda=\frac{\mathrm{h}}{\mathrm{m} v}$
$=\frac{\left(6.62 \times 10^{-34}\right)}{9.103939 \times 10^{-31} \mathrm{~kg}\left(1.6 \times 10^{6} \mathrm{~ms}^{-1}\right)}$
$=4.55 \times 10^{-10} \mathrm{~m} \lambda=455 \mathrm{pm}$
de Broglie's wavelength associated with the electron is $455 \mathrm{pm}$.
Question 57. Similar to electron diffraction, neutron diffraction microscope is also used for the determination of the structure of molecules. If the wavelength used here is $800 \mathrm{pm}$, calculate the characteristic velocity associated with the neutron.
Solution: Given: The wavelength used $=800 \mathrm{pm}$
We know: Planck's constant $=6.62 \times 10^{-34}$
Mass of the particle $=1.67 \times 10^{-27} \mathrm{~kg}$
From de Broglie's equation,
$\lambda=\frac{\mathrm{h}}{\mathrm{mv}}$
$v=\frac{h}{m \lambda}$
Where,
$\mathrm{v}=$ velocity of particle (neutron)
$\mathrm{h}=$ Planck's constant
$\mathrm{m}=$ mass of particle (neutron)
$\lambda=$ wavelength
Substituting the values in the expression of velocity (v),
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)}{\left(1.67 \times 10^{-27}\right)\left(800 \times 10^{-12} \mathrm{~m}\right)}$
$=4.94 \times 10^{2} \mathrm{~J}$
$=494 \mathrm{~ms}^{-1}$
Velocity associated with the neutron $=494 \mathrm{~ms}^{-1}$
Question 58. If the velocity of the electron in Bohr's first orbit is $2.19 \times 10^{6} \mathrm{~ms}^{-1}$, calculate the de Broglie wavelength associated with it.
Solution:
Given: velocity of the electron in first orbit $=2.19 \times 10^{6} \mathrm{~ms}^{-1}$
We know: The value of planck's constant $=6.62 \times 10^{-34}$
Formula: According to de Broglie's equation,
$\lambda=\frac{\mathrm{h}}{\mathrm{mv}}$
Where, $\lambda=$ wavelength associated with the electron
$\mathrm{h}=$ Planck's constant
$\mathrm{m}=$ mass of electron
$\mathrm{v}=$ velocity of electron Substituting the values in the expression of $\lambda$ :
$\lambda=\frac{h}{m v}$
$=\frac{\left(6.62 \times 10^{-34}\right)}{9.103939 \times 10^{-31} \mathrm{~kg}\left(2.19 \times 10^{6} \mathrm{~ms}^{-1}\right)}$
$=3.32 \times 10^{-10} \mathrm{~m} \lambda=332 \mathrm{pm}$
Question 59. The velocity associated with a proton moving in a potential difference of $1000 \mathrm{~V}$ is $4.37 \times 10^{5} \mathrm{~ms}^{-1}$. If the hockey ball of mass $0.1 \mathrm{~kg}$ is moving with this velocity, calculate the wavelength associated with this velocity.
Solution: Given: Potential difference $=1000 \mathrm{~V}$
Velocity of the proton $=4.37 \times 10^{5} \mathrm{~ms}^{-1}$
Mass of the hockey ball $=0.1 \mathrm{~kg}$
We know: Planck's constant $(\mathrm{h})=6.62 \times 10^{-34}$
Formula: According to de Broglie's expression,
$\lambda=\frac{\mathrm{h}}{\mathrm{m} v}$
$=\frac{\left(6.62 \times 10^{-34}\right)}{0.1 \mathrm{~kg}\left(4.37 \times 10^{5} \mathrm{~ms}^{-1}\right)}$
$=1.516 \times 10^{-38} \mathrm{~m}$
Question 60. If the position of the electron is measured within an accuracy of $+0.002 \mathrm{~nm}$, calculate the uncertainty in the momentum of the electron. Suppose the momentum of the electron is $\mathrm{h} / 4 \pi_{\mathrm{m}} \times 0.05 \mathrm{~nm}$, is there any problem in defining this value.
Solution: Given: Accuracy in measurement of position $=+0.002 \mathrm{~nm}$
Momentum of the electron $=\frac{\mathrm{h}}{4 \pi_{\mathrm{m}}} \times 0.05 \mathrm{~nm}$
From Heisenberg's uncertainty principle,
Where,
$\Delta \mathrm{x}=$ uncertainty in position of the electron
$\Delta \mathrm{p}=$ uncertainty in momentum of the electron
Substituting the values in the expression of $\Delta \mathrm{p}$ :
$=2.637 \times 10^{-23} \mathrm{Jsm}^{-1}$
$\Delta \mathrm{p}=2.637 \times 10^{-23} \mathrm{kgms}^{-1}\left(1 \mathrm{~J}=1 \mathrm{kgms} 2 \mathrm{~s}^{-1}\right)$
Uncertainty in the momentum of the electron $=2.637 \times 10^{-23} \mathrm{kgms}^{-1} .=$ $1.055 \times 10^{-24} \mathrm{kgms}^{-1}$
Since the magnitude of the actual momentum is smaller than the uncertainty, the value cannot be defined.
Question 61. The quantum numbers of six electrons are given below. Arrange them in order of increasing energies. If any of these combination (s) has/have the same energy lists:
1. $\mathrm{n}=4, \mathrm{l}=2, \mathrm{ml}=-2, \mathrm{~m}_{\mathrm{s}}=-1 / 2$
2. $\mathrm{n}=3, \mathrm{l}=2, \mathrm{ml}=1, \mathrm{~m}_{\mathrm{s}}=+1 / 2$
3. $\mathrm{n}=4, \mathrm{l}=1, \mathrm{ml}=0, \mathrm{~m}_{\mathrm{s}}=+1 / 2$
4. $\mathrm{n}=3, \mathrm{l}=2, \mathrm{ml}=-2, \mathrm{~m}_{\mathrm{s}}=-1 / 2$
5. $\mathrm{n}=3, \mathrm{l}=1, \mathrm{ml}=-1, \mathrm{~m}_{\mathrm{s}}=+1 / 2$
6. $\mathrm{n}=4, \mathrm{l}=1, \mathrm{ml}=0, \mathrm{~m}_{\mathrm{s}}=+1 / 2$
Solution: For $\mathrm{n}=4$ and $\mathrm{l}=2$, the orbital occupied is $4 \mathrm{~d}$.
For $\mathrm{n}=3$ and $\mathrm{l}=2$, the orbital occupied is $3 \mathrm{~d}$.
For $\mathrm{n}=4$ and $\mathrm{l}=1$, the orbital occupied is $4 \mathrm{p}$.
Hence, the six electrons i.e., $1,2,3,4,5$, and 6 are present in the $4 \mathrm{~d}, 3 \mathrm{~d}, 4 \mathrm{p}, 3 \mathrm{~d}, 3 \mathrm{p}$, and $4 \mathrm{p}$ orbitals respectively.
Therefore, the increasing order of energies is $5(3 p)<2(3 d)=4(3 \mathrm{~d})<$ $3(4 p)=6(4 p)<1(4 d)$
Question 62. The bromine atom possesses 35 electrons. It contains 6 electrons in $2 \mathrm{p}$ orbital, 6 electrons in $3 \mathrm{p}$ orbital and 5 electrons in $4 \mathrm{p}$ orbital. Which of these electron experiences the lowest effective nuclear charge?
Solution: Nuclear charge experienced by an electron (present in a multi-electron atom) is dependant upon the distance between the nucleus and the orbital, in which the electron is present. As the distance increases, the effective nuclear charge also decreases. Among p-orbitals, $4 \mathrm{p}$ orbitals are farthest from the nucleus of bromine atom with $(+35)$ charge. Hence, the electrons in the $4 \mathrm{p}$ orbital will experience the lowest effective nuclear charge. These electrons are shielded by electrons present in the $2 \mathrm{p}$ and $3 \mathrm{p}$ orbitals along with the s-orbitals. Therefore, they will experience the lowest nuclear charge.
Question 63. Among the following pairs of orbitals which orbital will experience the larger effective nuclear charge?
(i) $\quad 2$ s and $3 s$,
(ii) $4 \mathrm{~d}$ and $4 \mathrm{f}$,
(iii) $3 \mathrm{~d}$ and $3 \mathrm{p}$
Solution: Nuclear charge is defined as the net positive charge experienced by an electron in the orbital of a multi-electron atom. The closer the orbital, the greater is the nuclear charge experienced by the electron $(\mathrm{s})$ in it.
(i) The electron(s) present in the $2 \mathrm{~s}$ orbital will experience greater nuclear charge (being closer to the nucleus) than the electron(s) in the 3 s orbital.
(ii) 4 d will experience greater nuclear charge than $4 \mathrm{f}$ since $4 \mathrm{~d}$ is closer to the nucleus.
(iii) $3 p$ will experience greater nuclear charge since it is closer to the nucleus than $3 \mathrm{f}$.
Question 64. The unpaired electrons in $\mathrm{Al}$ and $\mathrm{Si}$ are present in $3 \mathrm{p}$ orbital. Which electrons will experience more effective nuclear charge from the nucleus?
Solution: Nuclear charge is defined as the net positive charge experienced by an electron in a multielectron atom. The higher the atomic number, the higher is the nuclear charge. Silicon has 14 protons while aluminium has 13 protons. Hence, silicon has a larger nuclear charge of $(+14)$ than aluminium, which has a nuclear charge of $(+13)$. Thus, the electrons in the $3 \mathrm{p}$ orbital of silicon will experience a more effective nuclear charge than aluminium.
Question 65. Indicate the number of unpaired electrons in:
(a) $\mathrm{P}$
(b) $\mathrm{Si}$
(c) $\mathrm{Cr}$
(d) $\mathrm{Fe}$
(e) $\mathrm{Kr}$
Solution: (a) Phosphorus (P):
We know: Atomic number of $\mathrm{P}=15$
The electronic configuration of $P$ is:
1 s 22 s $22 \mathrm{p} 63 \mathrm{~s} 23 \mathrm{p} 3$
The orbital picture of $\mathrm{P}$ can be represented as:
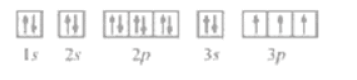
From the orbital picture, phosphorus has three unpaired electrons.
(b) Silicon (Si):
We know: Atomic number of $\mathrm{Si}=14$
The electronic configuration of Si is:
1s 22 s 22263 s $23 p 2$

From the orbital picture, silicon has two unpaired electrons.
(c) Chromium (Cr):
We know: Atomic number of $\mathrm{Cr}=24$
The electronic configuration of $\mathrm{Cr}$ is:
1 s $22 \mathrm{~s} 22 \mathrm{p} 63 \mathrm{~s} 23 \mathrm{p} 64 \mathrm{~s} 13 \mathrm{~d} 5$
The orbital picture of chromium is:
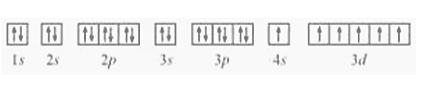
From the orbital picture, chromium has six unpaired electrons.
(d) Iron (Fe):
We know: Atomic number of $\mathrm{Fe}=26$
The electronic configuration is:
1 s 22 s2 2 p 63 s 23 p 64 s 2336
The orbital picture of chromium is:

From the orbital picture, iron has four unpaired electrons.
(e) Krypton (Kr):
We know: Atomic number of $\mathrm{Kr}=36$
The electronic configuration is:
$1 \mathrm{~s} 22 \mathrm{~s} 22 \mathrm{p} 63 \mathrm{~s} 23 \mathrm{p} 64 \mathrm{~s} 23 \mathrm{~d} 104 \mathrm{p} 6$
The orbital picture of krypton is:
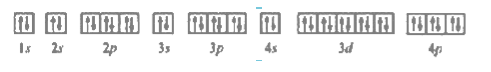
Since all orbitals are fully occupied, there are no unpaired electrons in krypton.
Question 66. (a) How many sub-shells are associated with $\mathrm{n}=4$ ?
(b) How many electrons will be present in the sub-shells having ms value of $-\frac{1}{2}$ for $\mathrm{n}=4$ ?
Solution: (a) Given: $\mathrm{n}=4$
For a given value of ' $\mathrm{n}$ ', ' 'l' can have values from zero to $(\mathrm{n}-1)$.
Therefore, $=0,1,2,3$
Thus, four sub-shells are associated with $\mathrm{n}=4$, which are $\mathrm{s}, \mathrm{p}, \mathrm{d}$ and $\mathrm{f}$.
(b) Given: $\mathrm{n}=4$
Number of orbitals in the $\mathrm{n}$ th shell $=\mathrm{n}^{2}$
For $\mathrm{n}=4$
Number of orbitals $=16$
If each orbital is taken fully, then it will have 1 electron with ms value of.
Therefore, Number of electrons with $\mathrm{m}_{\mathrm{s}}$ value of $(-12)$ is 16 .
Also Read,
Class 11 Chemistry Notes Free PDF Download.
Class 11 Chemistry Book Chapterwise Free PDF Download
Class 11 Chemistry Exemplar Chapterwise Free PDF Download
If you have any Confusion related to NCERT Solutions for Class 11 Chemistry chapter 2 Structure of Atom PDF then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 11 Chemistry by Kota’s top IITian’s Faculties Install the eSaral App
In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 2 Structure of Atom in PDF that are prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to learn and understand class 11 Chemistry chapter 2 "Structure of Atom" in an easy way then you can use these solutions PDF.
NCERT Solutions helps students to Practice important concepts of subjects easily. Class 11 Chemistry solutions provide detailed explanations of all the NCERT questions that students can use to clear their doubts instantly.
If you want to score high in your class 11 Chemistry Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.
In this article, we have listed NCERT Solutions for Class 11 Chemistry chapter 2 Structure of Atom PDF that you can download to start your preparations anytime.
So, without wasting more time Let’s start.
Download NCERT Solutions for Class 11 Chemistry chapter 2 Structure of Atom PDF
Question 1.Figure the quantity of electrons which will together measure one gram.
(b) Compute the mass and charge of one mole of electrons.
Solution: (a) We know : Mass of an electron $=9.10 \times 10^{-31} \mathrm{~kg}$
$\therefore$ Quantity of electrons that measure $9.10 \times 10^{-31} \mathrm{~kg}=1$
$\therefore$ Quantity of electrons that will measure $1 \mathrm{~g}\left(1 \times 10^{-3} \mathrm{~kg}\right)$
$=\frac{1}{9.1 \times 10^{-31} \mathrm{~kg}} \times\left(1 \times 10^{-3} \mathrm{~kg}\right)$
$=0.109 \times 10^{-3+31}$
$=0.1098 \times 10^{28}$
$=1.098 \times 10^{27}$
(b) (i) We know: Mass of one electron $=9.1 \times 10^{-31} \mathrm{~kg}$
Mass of one mole of electron $=9.1 \times 10^{-31} \mathrm{~kg} \times \mathrm{N}_{\mathrm{A}}=(6.023 \times$
$\left.10^{23}\right) \times\left(9.10 \times 10^{-31} \mathrm{~kg}\right)$
$=5.48 \times 10^{-7} \mathrm{~kg}$
Or
We know Mass of one electron $=9.1 \times 10^{-28} \mathrm{~g}$
The formula used: Mass of one mole of electron
$=$ Mass of one electron $\times \mathrm{N}_{\mathrm{A}}$
$=9.1 \times 10^{-28} \mathrm{~g} \times \mathrm{N}_{\mathrm{A}}$
$=\left(9.1 \times 10^{-28} \mathrm{~g}\right) \times\left(6.023 \times 10^{23}\right)$
$=5.48 \times 10^{-4} \mathrm{~g}$
We know: Charge on one electron $=1.6 \times 10^{-19}$ coulomb
Formula: Charge on one mole of electron $=$ Charge on one electron $\times \mathrm{N}_{\mathrm{A}}$
$=\left(1.6 \times 10^{-19} \mathrm{C}\right) \times \mathrm{N}_{\mathrm{A}}$
$=\left(1.6 \times 10^{-19} \mathrm{C}\right) \times\left(6.023 \times 10^{23}\right)$
$=9.65 \times 10^{4} \mathrm{C}$
Question 2. (I) Calculate the total number of electrons present in one mole of methane.
(II) Find (a) the total number and (b) the total mass of neutrons in $7 \mathrm{mg}$ of $14 \mathrm{c}$.
(Assume that mass of a neutron $=1.67 \times 10^{-27} \mathrm{~kg}$ ).
(III) Find (a) the total number and (b) the total mass of protons in $34 \mathrm{mg}$ of $\mathrm{NH}_{3}$ at STP.
Will the answer change if the temperature and pressure are changed?
Solution: (I) We know : the atomic number of carbon $=6$
The atomic number of hydrogen $=1$
Number of electrons present in 1 molecule of methane $\left(\mathrm{CH}_{4}\right)$
$1(6)+4(1)=10$
Formula used: Number of electrons present in 1 mole of methane
$=$ Number of electrons present in 1 molecule of methane $\times\left(N_{A}\right)$
By putting the above values the formula
$=$ Number of electrons present in 1 molecule of methane $\times 6.023 \times$ $10^{23}$
$=10 \times 6.023 \times 10^{23}=6.023 \times 10^{24}$
(II)
(a) Number of atoms of $14_{C}$ in 1 mole $=6.023 \times 10^{23}$
Since 1 atom of $14_{c}$ contains
Neutrons $=(14-6)=8$
The number of neutrons in $14 \mathrm{~g}$ of $14_{\mathrm{C}}=N_{\mathrm{A}} \times 8=6.023 \times 10^{23} \times 8$
Or, $14 \mathrm{~g}$ of $14_{\mathrm{C}}$ contains $\left(6.023 \times 10^{23} \times 8\right)$ neutrons.
Number of neutrons in $7 \mathrm{mg}\left(7 \times 10^{-3} \mathrm{gram}\right)$
$=\frac{6.023 \times 10^{23} \times 8 \times 7 \times 10^{-3}}{14}$
$=2.40 \times 10^{21}$
(b) (x) The mass of one neutron $=1.67 \times 10^{-24} \mathrm{~g}$
The mass of total neutrons in $7 \mathrm{~g}$ of $14_{\mathrm{C}}$
$=\left(2.4092 \times 10^{21}\right) \times\left(1.67 \times 10^{-24} \mathrm{~g}\right)$
$=4.02 \times 10^{-3} \mathrm{~g}$
(y) The mass of one neutron $=1.67 \times 10^{-27} \mathrm{~kg}$
The mass of total neutrons in $7 \mathrm{~g}$ of $14 \mathrm{c}$
$=\left(2.4092 \times 10^{21}\right)\left(1.67 \times 10^{-27} \mathrm{~kg}\right)$
$=4.0352 \times 10^{-6} \mathrm{~kg}$
(III)
(a) We know: 1 mole of $\mathrm{NH}_{3}=1(14)+3(1) \mathrm{g}$ of $\mathrm{NH}_{3}$
$=17 \mathrm{~g}$ of $\mathrm{NH}_{3}$
$=6.023 \times 10^{23}$ Molecules of $\mathrm{NH}_{3}$
Total number of protons present in 1 molecule of $\mathrm{NH}_{3}$
$=1(7)+3(1)$
$=10$
Number of protons in $6.023 \times 10^{23}$ molecules of $\mathrm{NH}_{3}$
$=\left(6.023 \times 10^{23}\right)(10)$
$=6.023 \times 10^{24}$
$\Rightarrow 17 \mathrm{~g}$ of $\mathrm{NH}_{3}$
Number of protons in $34 \times 10^{-3} \mathrm{~g}$ of $\mathrm{NH}_{3}$
$=\frac{6.023 \times 10^{24} \times 34 \times 10^{-3}}{17}$
$=1.2046 \times 10^{22}$ Protons
(b)(x) We know: Mass of one proton $=1.67 \times 10^{-24} \mathrm{~g}$
The total mass of protons in $34 \mathrm{mg}\left(34 \times 10^{-3} \mathrm{~g}\right.$ ) of
$\mathrm{NH}_{3}$
$=\frac{\left(1.67 \times 10^{-24} \mathrm{~g}\right) \times 6.023 \times 10^{24} \times 34 \times 10^{-3} g}{17}$
$=\left(1.67 \times 10^{-24} \mathrm{~g}\right)\left(1.2046 \times 10^{22}\right)$
$=2.01 \times 10^{-2} \mathrm{~kg}$
(y) $\quad$ Mass of one proton $=1.67 \times 10^{-27} \mathrm{~kg}$
The total mass of protons in $34 \mathrm{mg}$ of $\mathrm{NH}_{3}$
$=\left(1.67 \times 10^{-27} \mathrm{~kg}\right)\left(1.2046 \times 10^{22}\right)$
$=2.0176 \times 10^{-5} \mathrm{~kg}$
The quantity of protons, electrons, and neutrons in a particle is free of temperature what's more, weight conditions. Subsequently, the acquired qualities will stay unaltered if the temperature and weight are changed.
Question 3. What number of neutrons and protons are there in the following nuclei?
${ }_{6}^{13} \mathrm{C},{ }_{8}^{16} \mathrm{O},{ }_{12}^{24} \mathrm{Mg},{ }_{16}^{56} \mathrm{Fe},{ }_{38}^{88} \mathrm{Sr}$
Solution: A symbolic representation of an atom ${ }_{\mathrm{z}}^{\mathrm{A}} \mathrm{x}$ where $\mathrm{A}$ represents Atomic mass (number of proton and neutron) and $Z$ atomic number(number of proton )
${ }_{6}^{13} \mathrm{C}:$
Given: Atomic mass $(\mathrm{A})=13$
Atomic number $(\mathrm{Z})=$ Number of protons $=6$
Formula:Number of neutrons $=$ (Atomic mass)-(Atomic number)
$=13-6=7$
${ }_{8}^{16} \mathrm{O}:$
Given: Atomic mass $(\mathrm{A})=16$
Atomic number $(\mathrm{Z})=8$
Number of protons $=8$
Formula: Number of neutrons $=$ (Atomic mass)- (Atomic number)
$=16-8=8$
${ }_{12}^{24} \mathrm{Mg}:$
Given: Atomic mass $(\mathrm{A})=24$
Atomic number $(\mathrm{Z})=$ Number of protons $=12$
Formula: Number of neutrons $=$ (Atomic mass) - (Atomic number)
$=24-12=12$
${ }_{16}^{56} \mathrm{Fe}$ :
Given: Atomic mass $(\mathrm{A})=56$
Atomic number $(\mathrm{Z})=$ Number of protons $=26$
Formula: Number of neutrons $=$ (Atomic mass)-(Atomic number)
$=56-26=30$
${ }_{38}^{88} \mathrm{Sr}:$
Given: Atomic $\operatorname{mass}(\mathrm{A})=88$
Atomic number $(\mathrm{Z})=$ Number of protons $=38$
Formula: Number of neutrons $=$ (Atomic mass)-(Atomic number)
$=88-38=50$
Question 4. Compose the total image for the atom with the given nuclear number (Z) and Atomic mass (A)
(I) $\mathrm{Z}=17, \mathrm{~A}=35$
(II) $\mathrm{Z}=92, \mathrm{~A}=233$
(III) $\quad \mathrm{Z}=4, \mathrm{~A}=9$
Solution: Symbolic representation of an atom ${ }_{z}^{\mathrm{A}} \mathrm{x}$
(i) $\quad \mathrm{Z}=17, \mathrm{~A}=35:{ }_{17}^{35} \mathrm{C}$
(ii) $\mathrm{Z}=92, \mathrm{~A}=233:{ }_{92}^{233} \mathrm{U}$
(iii) $\mathrm{Z}=4, \mathrm{~A}=9:{ }_{4}^{9} \mathrm{Be}$
Question 5. Yellow light radiated from a sodium light has a wavelength $(\lambda)$ of $580 \mathrm{~nm}$. Ascertain the frequency ( $v$ ) and wave number $(\bar{v})$ of the yellow light.
Solution: given in question: $\mathrm{c}=$ velocity of light in vacuum $=3 \times 10^{8} \frac{\mathrm{m}}{\mathrm{s}}$
the wavelength of yellow light $(\lambda)=580 \mathrm{~nm}=580 \times 10^{-9} \mathrm{~m} / \mathrm{s}$
the formula used : wavelength $(\lambda)$
$=\frac{\text { velocity of light }(\mathrm{c})}{\text { frequency }(\mathrm{v})}$
From the expression we get,
$v=\frac{c}{\lambda} \quad \ldots \ldots \ldots$. $(1)$
Substituting the values in expression (1):
$v=\frac{3 \times 10^{8}}{580 \times 10^{-9}}=5.17 \times 10^{14} \mathrm{~s}^{-1}$
Thus, the frequency of yellow light emitted from the sodium lamp
$=5.17 \times 10^{14} \mathrm{~s}^{-1}$
The wave number of yellow light $\overline{(v)}=\frac{1}{\text { wavelength }(\lambda)}$
$=\frac{1}{580 \times 10^{-9}}=1.72 \times 10^{6} \mathrm{~m}^{-1}$
Question 6. Find energy of each of the photons which
(I) correspond to light of frequency $3 \times 10^{15} \mathrm{~Hz}$.
(II) Have a wavelength of $0.50$ angstrom.
Solution: (I) Given: light of frequency $=3 \times 10^{15} \mathrm{~Hz}$.
The formula used: Energy (E) of one photon $=$ hy
Where $\mathrm{h}=$ Planck's constant $=6.62 \times 10^{-34} \mathrm{Js}$
$v=$ frequency of light $=3 \times 10^{15} \mathrm{~Hz}$
Substituting the above values in the given formula of Energy:
$\mathrm{E}=\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(3 \times 10^{15} \mathrm{~Hz}\right)$
$\mathrm{E}=1.99 \times 10^{-18} \mathrm{~J}$
(II) Given: wavelength $=0.50$ angstrom
Energy (E) of a photon having wavelength $(\lambda)$ is given by the expression,
Formula: $\mathrm{E}=\mathrm{hv}=\frac{\mathrm{hc}}{\lambda}$
$\mathrm{h}=$ Planck's constant $=6.62 \times 10^{-34} \mathrm{Js}$
$\mathrm{c}=$ velocity of light in vacuum $=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$
we know: 1 angstrom $=10^{-10}$ meter
So $0.50$ angstrom $=0.50 \times 10^{-10}$ meter
Substituting the values in the given expression of Energy :
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{0.50 \times 10^{-10}}=3.97 \times 10^{-15} \mathrm{~J}$
$\therefore \mathrm{E}=3.97 \times 10^{-15} \mathrm{~J}$
Question 7. Calculate the wavelength, frequency and wave number of a light wave whose time period is $2.0 \times 10^{-10} \mathrm{~S}$
Solution: Given: time period of light $=2.0 \times 10^{-10} \mathrm{~s}$
The formula used: Frequency of light $(v)=\frac{1}{\text { time Period }}$
$=\frac{1}{2.0 \times 10^{-10} \mathrm{~s}}$
$=5.0 \times 10^{9} \mathrm{~s}^{-1}$
The formula used : Wavelength of light $(\lambda)$
$=\frac{\text { the velocity of light in a vacuum(c) }}{\text { Frequency of light (v) }}$
Where,
$\mathrm{c}=$ velocity of light in vacuum $=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$
Substituting the value in the given expression of $\lambda$ :
$\lambda=\frac{3 \times 10^{8} \mathrm{~m} / \mathrm{s}}{5.0 \times 10^{9} \mathrm{~s}^{-1}}=6.0 \times 10^{-2} \mathrm{~m}$
Wave number $(\bar{v})$ of light $=\frac{1}{\text { wave length }(\lambda)}$
$=\frac{1}{6.0 \times 10^{-2} m}=1.66 \times 10 \mathrm{~m}^{-1}=$
$16.66 \mathrm{~m}^{-1}$
Question 8. What is the quantity of photons of light with a wavelength of $4000 \mathrm{pm}$ that gives $1 \mathrm{~J}$ of energy?
Solution: Given: wavelength of light $=4000 \mathrm{pm}$
energy $=1 \mathrm{~J}$
Formula: Energy (E) of one photon
$=$ Planck's constant (h) $\times$ frequency of light (v)
frequency of light (v) $=\frac{\text { velocity of light }(c)}{\text { wave length }(\lambda)}$
Energy $\left(\mathrm{E}_{n}\right)$ of ' $n$ ' photons $=n h v \Rightarrow n=\frac{E_{n} \lambda}{h c}$
Where the wavelength of light $(\lambda)=4000 \mathrm{pm}=4000 \times 10^{-12} \mathrm{~m}$
The velocity of light in a vacuum $(\mathrm{c})=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$
Planck's constant $(h)=6.62 \times 10^{-34} \mathrm{Js}$
Substituting the values in the given expression of $\mathrm{n}$ :
$\mathrm{n}=\frac{1 \times\left(4000 \times 10^{-12}\right)}{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}=2.01 \times 10^{16}$
Hence, the number of photons with a wavelength of $4000 \mathrm{pm}$ and energy of $1 \mathrm{~J}$ is $2.01 \times 10^{16}$
Question 9. A photon of wavelength $4 \times 10^{-7} \mathrm{~m}$ strikes on metal surface, the work function of the metal being $2.13 \mathrm{eV}$. Calculate
(I) the energy of the photon (eV),
(II) the kinetic energy of the emission, and
(III) the velocity of the photoelectron $\left(1 \mathrm{eV}=1.6020 \times 10^{-19} \mathrm{~J}\right)$
Solution: Given: wavelength of photon $=4 \times 10^{-7} \mathrm{~m}$
work function of the metal $=2.13 \mathrm{eV}$
The energy of one photon
Formula:(E) $=$ Planck's constant $(\mathrm{h}) \times$ frequencyof light $(v)$
$=\frac{\text { Planck's constant }(\mathrm{h}) \times \text { velocity of light (c) }}{\text { wave length of light }(\lambda)}$
Where Planck's constant $(h)=6.62 \times 10^{-34} \mathrm{Js}$
the velocity of light in a vacuum $(c)=3 \times 10^{8} \mathrm{~m} / \mathrm{s} \lambda=$ the wavelength of a photon $(\lambda)=4 \times 10^{-7} \mathrm{~m} / \mathrm{s}$
Substituting the values in the given expression of $E$ :
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{4 \times 10^{-7}}=4.965 \times 10^{-19} \mathrm{~J}$
$\mathrm{Or}=\left(\frac{4.965 \times 10^{-19}}{1.6020 \times 10^{-19}}\right) \mathrm{eV}=3.10 \mathrm{eV}$
Hence, the energy of the photon is $4.97 \times 10^{-19} \mathrm{~J}$ or $3.1020 \mathrm{eV}$
(II) Formula: The kinetic energy of emission $\mathrm{E}_{\mathrm{k}}=\mathrm{hv}-\mathrm{hv}_{0}$
$=(\mathrm{E}-\mathrm{W}) \mathrm{eV}$
$=(3.1020-2.13) \mathrm{eV}$
$=0.9720 \mathrm{eV}$
Hence, the kinetic energy of emission $\left(h v-h v_{0}\right)=0.97 \mathrm{eV}$
$=0.97 \mathrm{eV} \times 1.6020 \times 10^{-19} \mathrm{~J}$
$=1.55 \times 10^{-19} \mathrm{~J}$
(III) Formula: The velocity of a photoelectron (v) can be calculated by the expression,
$\frac{1}{2} \mathrm{mv}^{2}=\mathrm{hv}-\mathrm{h} v_{0}$
$\Rightarrow v=\sqrt{\frac{2\left(h v-h v_{0}\right)}{m}}$
Where $\left(h v-h v_{0}\right)$ is the kinetic energy of emission in Joules = $1.55 \times 10^{-19} \mathrm{~J}$
$' \mathrm{~m}$ ' is the mass of the photoelectron $=9.10939 \times 10^{-31} \mathrm{~kg}$
Substituting the values in the given expression of $\mathrm{v}$ :
$v=\frac{\sqrt{2 \times 1.55 \times 10^{-19} \mathrm{~J}}}{9.10939 \times 10^{-31} \mathrm{~kg}}$
$=\sqrt{0.3418 \times 10^{12} \mathrm{~m}^{2} \mathrm{~s}^{2}}$
$\Rightarrow \mathrm{v}=5.84 \times 10^{5} \mathrm{~ms}^{-1}$
Hence, the velocity of the photoelectron is $5.84 \times 10^{5} \mathrm{~ms}^{-1}$
Question 10. Electromagnetic radiation of wavelength $242 \mathrm{~nm}$ is just sufficient to ionise the sodium atom. Calculate the ionization energy of sodium in $\mathrm{kJ} \mathrm{mol}^{-1}$.
Solution: Given: wavelength of Electromagnetic radiation $(\lambda)=242 \mathrm{~nm}=242 \times 10^{-9} \mathrm{~m}$
Formula used: Energy of sodium atom $(\mathrm{E})=\frac{\mathrm{N}_{\mathrm{A} \mathrm{hc}}}{\lambda}$
Where, Avogadro's number $\left(\mathrm{N}_{\mathrm{A}}\right)=6.023 \times 10^{23}$
Planck's constant $(h)=6.62 \times 10^{-34} \mathrm{Js}$
the velocity of light in vacuum $(c)=3 \times 10^{8}$ meter $/ \mathrm{sec}$
$\mathrm{E}=\frac{\left(6.023 \times 10^{23}\right)\left(6.62 \times 10^{-34}\right) \mathrm{Js}\left(3 \times 10^{8}\right) \mathrm{ms}^{-1}}{242 \times 10^{-9} \mathrm{~m}}$
$=4.947 \times 10^{5} \mathrm{Jmol}^{-1}$
$=494.7 \times 10^{3} \mathrm{Jmol}^{-1}$
$=494 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}$
Question 11. A 25 -watt bulb discharges monochromatic yellow light of a wavelength of $0.57 \mu \mathrm{m}$. Ascertain the rate of discharge of quanta every second.
Solution: Given:
Power of bulb, $P=25$ Watt $=25 \mathrm{Js}^{-1}$
Wavelength $(\lambda)=0.57 \mu \mathrm{m}=0.57 \times 10^{-6}$ meter
Formula: Energy of one photon, $\mathrm{E}=\mathrm{hv}=\frac{\mathrm{hc}}{\lambda}$
Substituting the values in the given expression of E:
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(0.57 \times 10^{-6}\right)}=34.87 \times 10^{-20} \mathrm{~J}$
Rate of emission of quanta per second
$=\frac{\text { power }}{\text { Energy }}=\frac{25}{34.87 \times 10^{-20}}=7.17 \times 10^{19} \mathrm{~s}^{-1}$
Question 12. Electrons are discharged with zero speed from a metal surface when it is presented to radiation of wavelength $6800 A$. Figure limit recurrence $\left(v_{0}\right)$ and work $\left(\mathrm{W}_{0}\right)$ of the metal.
Solution: Given: Threshold wavelength of radiation $\left(\lambda_{0}\right)=6800 A =6800 \times$ $10^{-10} \mathrm{~m}=6.8 \times 10^{-7} \mathrm{~m}$
Formula: Threshold frequency $\left(v_{0}\right)$ of the metal $=\frac{c}{\lambda_{0}}$
$=\frac{3 \times 10^{8} \mathrm{~ms}^{-1}}{6.8 \times 10^{-7} \mathrm{~m}}=4.41 \times 10^{14} \mathrm{~s}^{-1}$
Thus, the threshold frequency $\left(v_{0}\right)$ of the metal $=\mathrm{hv}_{0}$
$=\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(4.41 \times 10^{14} \mathrm{~s}^{-1}\right)$
$=2.922 \times 10^{-19} \mathrm{~J}$
Question 13. What is the wavelength of light transmitted when the electron in a hydrogen atom experiences move from an energy level with $\mathrm{n}=4$ to an energy level with $\mathrm{n}=2 ?$
Solution: Formula: The $n_{i}=4$ to $n_{f}=2$ transition will give rise to a spectral line of the Balmer series. The energy involved in the transition is given by the relation,
$\mathrm{E}=2.18 \times 10^{-18}\left[\frac{1}{\mathrm{n}_{\mathrm{i}}^{2}}-\frac{1}{\mathrm{n}_{\mathrm{f}}^{2}}\right] \mathrm{J}$
Substituting the values in the given expression of $E$ :
$\mathrm{E}=2.18 \times 10^{-18}\left[\frac{1}{4^{2}}-\frac{1}{2^{2}}\right] J$
$\mathrm{E}=2.18 \times 10^{-18}\left[\frac{1}{16}-\frac{1}{4}\right] J$
$=2.18 \times 10^{-18}\left[\frac{1-4}{16}\right] \mathrm{J}$
$=2.18 \times 10^{-18} \times\left(-\frac{3}{16}\right) \mathrm{J}$
$\mathrm{E}=-\left(4.09 \times 10^{-19} \mathrm{~J}\right)$
The negative sign indicates the energy of emission.
formula used: $E=\frac{h c}{\text { wave length }(\lambda)}$
$\therefore$ Wavelength of light emitted $(\lambda)=\frac{\mathrm{hc}}{\mathrm{E}}$
Where, Avogadro's number $\left(\mathrm{N}_{\mathrm{A}}\right)=6.023 \times 10^{23}$
Planck's constant $(h)=6.62 \times 10^{-34} \mathrm{Js}$
the velocity of light in vacuum $(c)=3 \times 10^{8}$ meter $/ \mathrm{sec}$
Substituting the values given above in the formula of Wavelength of light emitted
$\lambda=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(4.0875 \times 10^{-19}\right)}$
$=4.8631 \times 10^{-7} \mathrm{~m}$
$\lambda=486.31 \times 10^{-9} \mathrm{~m} \quad\left(\therefore 10^{-9} \mathrm{~m}=1 \mathrm{~nm}\right)$
$=486 \mathrm{~nm}$
Question 14. What amount of energy is required to ionize a H molecule if the electron involves $\mathrm{n}=5$ circle? Contrast your answer and the ionization enthalpy of $\mathrm{H}$ molecule (energy required to evacuate the electron from $\mathrm{n}=1$ circle).
Solution: Given: principle quantum number $=5$
atomic number of $\mathrm{H}=1$
Formula: The expression of energy is given by,
$\mathrm{E}_{\mathrm{n}}=-\frac{(13.6) \mathrm{Z}^{2}}{\mathrm{n}^{2}} \mathrm{eV}$
$\left(\therefore 1 \mathrm{eV} \times 1.6 \times 10^{-19}=1 \mathrm{~J}\right)$
$=-\frac{\left(2.18 \times 10^{-18}\right) \mathrm{z}^{2}}{\mathrm{n}^{2}} \mathrm{~J}$
Where,
$\mathrm{Z}=$ atomic number of the atom $\mathrm{n}$
$\mathrm{n}=$ principal quantum number
For ionization from $\mathrm{n}_{1}=5$ to $\mathrm{n}_{2}=\infty$,
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{5}$
$=\left[\left(\frac{-(13.6)(1)^{2}}{(\infty)^{2}}\right)-\left(\frac{-(13.6)(1)^{2}}{(5)^{2}}\right)\right] \mathrm{eV}$
$=0.544 \mathrm{eV}$
$\left(\therefore 1 e v \times 1.6 \times 10^{-19}=1 \mathrm{~J}\right)$
$=0.544 \mathrm{eV} \times 1.6 \times 10^{-19} \mathrm{~J}$
$=0.08704 \times 10^{-18} \mathrm{~J}$
$\Delta \mathrm{E}=8.70 \times 10^{-20} \mathrm{~J}$
Hence, the energy required for ionization from $\mathrm{n}=5$ to $\mathrm{n}=\infty$ is
$\Delta \mathrm{E}=8.70 \times 10^{-20} \mathrm{~J}$
Energy required for $\mathrm{n}_{1}=1$ to $\mathrm{n}_{2}=\infty$,
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{5}$
$=\left[\left(\frac{-13.6(1)^{2}}{(\infty)^{2}}\right)-\left(\frac{-13.6(1)^{2}}{(1)^{2}}\right)\right] \mathrm{eV}$
$=13.6 \mathrm{eV}$
$\left(\therefore 1 \mathrm{eV} \times 1.6 \times 10^{-19}=1 \mathrm{~J}\right)$
$=13.6 \mathrm{eV} \times 1.6 \times 10^{-19} \mathrm{~J}$
$=2.18 \times 10^{-18} \mathrm{~J}$
$\Delta \mathrm{E}=2.18 \times 10^{-18} \mathrm{~J}$
Hence, less energy is required to ionize an electron in the $5^{t h}$ orbital of the hydrogen atom as compared to that in the ground state.
Question 15. When the excited electron of an $\mathrm{H}$ atom in $\mathrm{n}=6$ drops to the ground state, the following transitions are possible:
Solution: Hence, the total number of $(5+4+3+2+1) 15$ lines will be obtained in the emission spectrum.

Alternative method:
Formula : The number of spectral lines produced when an electron in the $n^{t h}$ leVel drops down to the ground state
$\frac{n(n-1)}{2}$
Given, $n=6$
Number of spectral lines $=\frac{6(6-1)}{2}=15$
Question 16. (I) Energy associated with the fifth orbit of a hydrogen atom is calculated as:
Solution: Given: hydrogen orbit $(\mathrm{n})=5$
for hydrogen atomic number $(\mathrm{Z})=1$
$\mathrm{E}_{5}=\frac{-(13.6)(\mathrm{Z})^{2}}{(\mathrm{n})^{2}} \mathrm{eV}$
$=\frac{-(13.6)}{(5)^{2}} \mathrm{eV}$
$=\frac{-(13.6)}{25} \mathrm{eV}$
$=2.72 \mathrm{eV}$
$\left(\therefore 1 \mathrm{eV} \times 1.6 \times 10^{-19}=1 \mathrm{~J}\right)$
$=2.72 \mathrm{eV} \times 1.6 \times 10^{-19} \mathrm{~J}$
$=-8.72 \times 10^{-20} \mathrm{~J}$
(II) The radius of Bohr's $n^{t h}$ orbit for atom $\left(\mathrm{r}_{\mathrm{n}}\right)=\frac{(0.0529) \mathrm{n}^{2}}{z} \mathrm{~nm}$
Solution: We know: Hydrogen atom $\mathrm{Z}=1$
Radius For $\mathrm{n}=5$
$\mathrm{r}_{\mathrm{s}}=\frac{(0.0529) \mathrm{n}^{2}}{z}$
$r_{5}=(0.0529) \times(5)^{2} \mathrm{~nm}$
$\mathrm{r}_{5}=(0.0529) \times(25) \mathrm{nm}$
$\mathrm{r}_{5}=1.3225 \mathrm{~nm} \cong 1.32 \mathrm{~nm}$
Question 17. Calculate the wave number for the longest wavelength transition in the Balmer series of atomic hydrogen.
Solution: For the Balmer series, $n_{1}=2$. Thus, the expression of wavenumber $(\bar{v})$ is given by,
$\bar{v}=\left[\frac{1}{(2)^{2}}-\frac{1}{\mathrm{n}_{\mathrm{f}}^{2}}\right]\left(1.097 \times 10^{7} \mathrm{~m}^{-1}\right)$
Formula: Wave number $(\bar{v}) \propto \frac{1}{\text { wavelength of transition }}$.
Hence, for the longest wavelength transition, Wave number $(\bar{v})$ has to be the smallest.
For $(\bar{v})$ to be minimum, $\mathrm{n}_{2}$ should be minimum.
For the Balmer series, a transition from $\mathrm{n}_{1}=2$ to $\mathrm{n}_{2}=3$ is allowed.
Hence, taking $\mathrm{n}_{2}=3$, we get:
$\bar{v}=\left(1.097 \times 10^{7}\right)\left[\frac{1}{(2)^{2}}-\frac{1}{3^{2}}\right]$
$\bar{v}=\left(1.097 \times 10^{7}\right)\left[\frac{1}{4}-\frac{1}{9}\right]$
$=\left(1.097 \times 10^{7}\right)\left[\frac{9-4}{36}\right]$
$=\left(1.097 \times 10^{7}\right)\left[\frac{5}{36}\right]$
$\bar{v}=1.52 \times 10^{6} \mathrm{~m}^{-1}$
Question 18. What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the light emitted when the electron returns to the ground state?
The ground-state electron energy is $-2.18 \times 10^{-11}$ ergs.
Solution: Energy (E) of the $\mathrm{n}^{\text {th }}$ Bohr orbit of an atom is given by
$\mathrm{E}_{5}=\frac{-\left(2.18 \times 10^{-18}\right) \mathrm{Z}^{2}}{(\mathrm{n})^{2}}$
Where $\mathrm{Z}=$ atomic number of the atom
Ground state energy $=-2.18 \times 10^{-11}$ ergs
$=-2.18 \times 10^{-11} \times 10^{-7} \mathrm{~J}$
$\left(\therefore 1\right.$ erg $\left.=10^{-7} \mathrm{~J}\right)$
$=-2.18 \times 10^{-18} \mathrm{~J}$
The energy required to shift the electron from $\mathrm{n}=1$ to $\mathrm{n}=5$ is given as:
$\Delta \mathrm{E}=\mathrm{E}_{5}-\mathrm{E}_{1}$
$=\left[\left(\frac{-\left(2.18 \times 10^{-18} \mathrm{~J}\right)(1)^{2}}{(5)^{2}}\right)-\left(\frac{-2.18 \times 10^{-18}}{1}\right)\right]$
$=\left[\left(\frac{-\left(2.18 \times 10^{-18} \mathrm{~J}\right)(1)^{2}}{25}\right)-\left(\frac{-2.18 \times 10^{-18}}{1}\right)\right]$
$=\left(2.18 \times 10^{-18}\right)\left[1-\frac{1}{25}\right]$
$=\left(2.18 \times 10^{-18}\right)\left[\frac{24}{25}\right]$
$=2.09 \times 10^{-18} \mathrm{~J}$
The wavelength of emitted light $(\lambda)=\frac{h c}{E}$
$\lambda=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(2.0928 \times 10^{-18}\right)}$
$\lambda=9.50 \times 10^{-8} \mathrm{~m}$
Question 19. The electron energy in hydrogen atom is given by $\mathrm{E}_{\mathrm{n}}=\frac{-2.18 \times 10^{-18}}{\mathrm{n}^{2}} \mathrm{~J}$ Calculate the energy required to remove an electron completely from the $\mathrm{n}=2$ orbit. What is the longest wavelength of light in $\mathrm{cm}$ that can be used to cause this transition?
Solution: $\mathrm{E}_{\mathrm{n}}=\frac{-\left(2.18 \times 10^{-18}\right)}{(\mathrm{n})^{2}} \mathrm{~J}$
The energy required for ionization from $\mathrm{n}=2$ is given by,
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{2}$
$=\left[\left(\frac{-2.18 \times 10^{-18}}{(\infty)^{2}}\right)-\left(\frac{\left(-2.18 \times 10^{-18}\right)}{(2)^{2}}\right)\right] \mathrm{J}$
$=\left[\frac{2.18 \times 10^{-18}}{4}-0\right] \mathrm{J}$
$\Delta \mathrm{E}=5.45 \times 10^{-19} \mathrm{~J}$
$\lambda=\frac{h c}{\Delta E}$
plank constant $(\mathrm{h})=6.62 \times 10^{-34}$
velocity of light $(\mathrm{c})=3 \times 10^{8}$
Here, $\lambda$ is the longest wavelength causing the transition.
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(0.57 \times 10^{-6}\right)}=34.87 \times 10^{-20} \mathrm{~J}$
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(5.45 \times 10^{-19}\right)}=3.647 \times 10^{-7} \mathrm{~m}$
$=3647 \times 10^{-10}$ meter
$\left(\therefore 10^{-10}\right.$ meter $= 1$Å)
$=3647 Å$
Question20. Calculate the wavelength of an electron moving with a velocity of $2.05 \times$ $10^{7} \mathrm{~ms}^{-1}$
Solution: Given: A mass of the particle $(\mathrm{m})=9.10939 \times 10^{-31} \mathrm{~kg}$
velocity of particle $(\mathrm{v})=2.05 \times 10^{7} \mathrm{~ms}^{-1}$
To find : wavelength of moving the particle $(\lambda)=?$
Formula used : According to de Broglie's equation,
wave length $(\lambda)=\frac{h}{p}=\frac{h}{m v}$
Planck's constant $(\mathrm{h})=\left(6.62 \times 10^{-34}\right) \mathrm{Js}$
Substituting the above values in the expression of $\lambda:$
$\lambda=\frac{\left(6.62 \times 10^{-34}\right) \mathrm{Js}}{\left(9.10939 \times 10^{-31} \mathrm{~kg}\right)\left(2.05 \times 10^{7} \mathrm{~ms}^{-1}\right)}$
$=3.55 \times 10^{-11} \mathrm{~m}$
Question 21. The mass of an electron is $9.1 \times 10^{-31} \mathrm{~kg}$. If its K.E. is $3.0 \times 10^{-25} \mathrm{~J}$, calculate its wavelength.
Solution: Given: The mass of an electron $=9.1 \times 10^{-31} \mathrm{~kg}$
K.E. of electron $=3.0 \times 10^{-25} \mathrm{~J}$
From de Broglie's equation,
wave length $(\lambda)=\frac{\mathrm{h}}{\mathrm{mv}}$
$h=\left(6.62 \times 10^{-34}\right) \mathrm{Js}$
Given, Kinetic energy $(\mathrm{K} . \mathrm{E})$ of the electron $=3.0 \times 10^{-25} \mathrm{~J}$
Since $\mathrm{K} . \mathrm{E} .=\frac{1}{2} \mathrm{~m} v^{2}$
$\therefore \operatorname{Velocity}(\mathrm{v})=\frac{\frac{\sqrt{2 \mathrm{~K} E}}{\mathrm{~m}}}{1}$
$=\sqrt{\frac{2 \times\left(3.0 \times 10^{-25} \mathrm{~J}\right)}{9.10939 \times 10^{-31} \mathrm{~kg}}}$
$=\sqrt{6.5866 \times 10^{4}}$
$\mathrm{v}=811.58 \mathrm{~ms}^{-1}$
Substituting all values in the expression of $\lambda$ :
$\lambda=\frac{\left(6.62 \times 10^{-34}\right) \mathrm{Js}}{\left(9.10939 \times 10^{-31} \mathrm{~kg}\right)\left(811.579 \mathrm{~ms}^{-1}\right)}$
$=8.9544 \times 10^{-7} \mathrm{~m} \cong 8.95 \times 10^{-7} \mathrm{~m}$
Question 22. (I) Write the electronic configurations of the following ions:
(a) $\mathrm{H}^{-}$
(b) $\mathrm{Na}^{+}$
(c) $\mathrm{O}_{2}^{-}$
(d) $\mathrm{F}^{-}$
(II) What are the atomic numbers of elements whose outermost electrons are represented by
(a) $3 \mathrm{~s}^{1}$
(b) $2 \mathrm{p}^{3}$ and
(c) $3 \mathrm{p}^{5}$
(III) Which atoms are indicated by the following configurations?
(a) [He] $2 \mathrm{~s}^{1}$
(b) $[\mathrm{Ne}] 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}$
(c) $\quad[\mathrm{Ar}] 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}$
Solution: (I) (a) $\mathrm{H}^{-}$ ion :
The atomic number of $\mathrm{H}$ - atom is
The electronic configuration of the $\mathrm{H}$ atom is $1 \mathrm{~s}^{1}$.
A negative charge on the species indicates the addition of an electron by it.
$\therefore$ Electronic configuration of $\mathrm{H}^{-}=1 \mathrm{~s}^{2}$
(b) $\mathrm{Na}^{+}$ ion :
The atomic number of Na-atom is 11
The electronic configuration of the Na atom is $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{1}$.
A positive charge on the species indicates the loss of an electron by it.
$\therefore$ Electronic configuration of $\mathrm{Na}^{+}=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{0}$ or
$1 s^{2} 2 s^{2} 2 p^{6}$
(c) $\mathrm{O}^{2-}$ ion:
The atomic number of $\mathrm{O}-$ atom is 8
The electronic configuration of $\mathrm{O}$ atom is $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{4}$.
A dinegative charge on the species indicates that two electrons are gained by it. $\therefore$ Electronic configuration of $0^{2-}$ ion $=1 s^{2} 2 s^{2} 2 p^{6}$
(d) $\mathrm{F}^{-}$ ion:
The atomic number of $\mathrm{F}$ - atom is 9
The electronic configuration of the $\mathrm{F}$ atom is $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{5}$.
A negative charge on the species indicates the gain of an electron by it.
$\therefore$ Electron configuration of $\mathrm{F}^{-}$ ion $=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6}$
(II) the electron configuration of the element as $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{6} 3 \mathrm{~d}^{6} 4 \mathrm{~s}^{2} \ldots \ldots$
(a) for $3 \mathrm{~s}^{1}$ the inner orbital 1 s2s $2 \mathrm{p}$ should be fulfilled
So the electron configuration of the element $=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{1}$
Number of electrons present in the atom of the element $=2+2+$ $6+1=11$
$\therefore$ The atomic number of the element $=11$
(b) for $2 \mathrm{p}^{3}$ the inner orbital $1 \mathrm{~s} 2 \mathrm{~s}$ should be fulfilled
Completing the electron configuration of the element as $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{3}$
Number of electrons present in the atom of the element $=2+2+$ $3=7$
$\therefore$ The atomic number of the element $=7$
(c) $2 \mathrm{p}^{5}$ the inner orbital $1 \mathrm{~s}, 2 \mathrm{~s}$ should be fulfilled
Completing the electron configuration of the element as $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{5}$
Number of electrons present in the atom of the element $=2+2+$ $5=9$
$\therefore$ Atomic number of the element $=9$
(III) (a) $[\mathrm{He}] 2 \mathrm{~s}^{1}$
The electronic configuration of the element $[\mathrm{He}]=1 \mathrm{~s}^{2}$
The electronic configuration of the element is $[\mathrm{He}] 2 \mathrm{~s}^{1}=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{1}$.
$\therefore$ Atomic number of the element $=3$
Hence, the element with the electronic configuration $[\mathrm{He}] 2 \mathrm{~s}^{1}$ is lithium (Li).
(b) $[\mathrm{Ne}] 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}$
The electronic configuration of the element
$[\mathrm{Ne}] 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6}$
The electronic configuration of the element is $[\mathrm{Ne}]=$ $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}$
$\therefore$ Atomic number of the element $=15$
Hence, the element with the electronic configuration $[\mathrm{Ne}] 3 \mathrm{~s}^{2} 3 \mathrm{p}^{3}$ is phosphorus (P).
(c) $[\mathrm{Ar}] 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}$
The electronic configuration of the element
$[\mathrm{Ar}]=1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{6}$
The electronic configuration of the element is $[\mathrm{Ar}] 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}=$ $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{6} 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}$
$\therefore$ Atomic number of the element $=21$
Hence, the element with the electronic configuration $[\mathrm{Ar}] 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{1}$ is scandium $(\mathrm{Sc})$.
Question 23. What is the most reduced estimation of $n$ that permits $g$ orbitals to exist?
Solution: For g-orbitals, $l=4$.
Azimuthal quantum number (l) value $=0$ to $(\mathrm{n}-1)$
"n" of principal quantum number,
$\therefore$ For $\mathrm{l}=4$, least value of $\mathrm{n}=5$
Question 24. An electron is in one of the $3 \mathrm{~d}$ orbitals. Give the possible values of $\mathrm{n}, \mathrm{l}$ and $\mathrm{ml}$ for this electron.
Solution: For the $3 \mathrm{~d}$ orbital:
Principal quantum number $(\mathrm{n})=3$
Azimuthal quantum number (l) $=(\mathrm{n}-1)=3-1=2$
Magnetic quantum number $\left(\mathrm{m}_{1}\right)=+\mathrm{l}$ to $-\mathrm{l}=-2,-1,0,1,2$
Question 25. An atom of an element contains 29 electrons and 35 neutrons. Deduce
(i) The number of protons and
(ii) The electronic configuration of the element.
Solution: (i) For an atom to be neutral, the number of protons is equal to the number of electrons.
$\therefore$ Number of protons in the atom of the given element $=29$
(ii) Number of protons in the atom of the given element $=29$
So The electronic configuration of the atom is $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{p}^{6} 4 \mathrm{~s}^{2} 3 \mathrm{~d}^{10}$.
Question 26. Give the number of electrons in the species, $\mathrm{H}_{2}^{+}$ and $\mathrm{H}_{2}$ and $\mathrm{O}_{2}^{+}$
Solution: Atomic number of $\mathrm{H}$ -atom $=1$
In hydrogen atom : Number of proton $=$ Number of electrons $=1$
Number of electrons present in hydrogen molecule $\left(H_{2}\right)=1+1=2$
$\mathrm{H}_{2} \rightarrow \mathrm{H}_{2}^{+}+e^{-}$
$\therefore$ Number of electrons in $\left(\mathrm{H}_{2}^{+}\right)$ molecule $=2-1=1$
$\mathrm{O}_{2}^{+}:$ Atomic number of $\mathrm{O}$ -atom $=8$
In hydrogen atom : Number of proton $=$ Number of electrons $=8$
Number of electrons present in oxygen molecule $\left(\mathrm{O}_{2}\right)=8+8=16$
$\mathrm{O}_{2} \rightarrow \mathrm{O}_{2}^{+}+e^{-}$
$\therefore$ Number of electrons in $\mathrm{O}_{2}^{+}=16-1=15$
Question 27. (I) An atomic orbital has $\mathrm{n}=3$. What are the possible values of $\mathrm{l}$ and $\mathrm{m}_{1}$ ?
(II) List the quantum numbers $\left(\mathrm{m}_{1}\right.$ and $\mathrm{l}$ ) of electrons for $3 \mathrm{~d}$ orbital.
(iii) Which of the following orbitals are possible? $1 \mathrm{p}, 2 \mathrm{~s}, 2 \mathrm{p}$ and $3 \mathrm{f}$
Solution: (I) $\quad \mathrm{n}=3$ (Given)
For a given value of $\mathrm{n}, \mathrm{l}$ can have values from 0 to $(\mathrm{n}-1)$.
$\therefore$ For $\mathrm{n}=3$
l value $=0$ to $(\mathrm{n}-1)=0,1,2$
For a given value of $1, \mathrm{ml}$ can have $(2 \mathrm{l}+1)$ values.
for $1=0$ value, $m_{0}=(2 l+1)=(2 x 0=1)$
$=1$ value $=$ so $\mathrm{m}=0$
for $\mathrm{l}=1$ value, $\mathrm{m}_{1}=(2 \mathrm{l}+1)=(2 \mathrm{x} 1=1)$
$=3$ value $=$ so $\mathrm{m}=-1,0,1$
for $1=2$ value, $m_{2}=(2 l+1)=(2 x 2=1)=5$ value
so, $\mathrm{m}=-2,-1,0,1,2$
(II) For 3 d orbital,
1 value $=0$ to $(\mathrm{n}-1)$
$\mathrm{n}=3$ so $\mathrm{l}=2$
For a given value of $1, \mathrm{~m}$ value $=(2 \mathrm{l}+1)=(2 \mathrm{x} 2+1)=5$
For $\mathrm{l}=2, \mathrm{~m}=-2,-1,0,1,2$
(III) Among the given orbitals only $2 \mathrm{~s}$ and $2 \mathrm{p}$ are possible. $1 \mathrm{p}$ and $3 \mathrm{f}$ cannot exist. For $p$ -orbital, $l=1$.
For a given value of $n, l$ can have values from 0 to $(\mathrm{n}-1)$.
For $\mathrm{l}=1$, the minimum value of $\mathrm{n}=2$
Similarly,
For f-orbital, $\mathrm{l}=4$
For $\mathrm{l}=4$, the minimum value of $\mathrm{n}=5$
$\mathrm{P}$ orbital should be started with $\mathrm{n}=2$ and $\mathrm{f}$ orbital should be started with $\mathrm{n}=5$ Hence, $1 \mathrm{p}$ and $3 \mathrm{f}$ do not exist.
Question 28. Using s, p, d notations, describe the orbital with the following quantum numbers.
(a) $\mathrm{n}=1, \mathrm{l}=0$
(b) $\quad \mathrm{n}=3 ; 1=1$;
(c) $\quad \mathrm{n}=4 ; \mathrm{l}=2$;
(d) $\quad \mathrm{n}=4 ; 1=3$;
Solution: (a) $\mathrm{n}=1, \mathrm{l}=0$ is for s orbital hence The orbital is $1 \mathrm{~s}$.
(b) For $\mathrm{n}=3$ and $\mathrm{l}=1$ for $\mathrm{p}$ orbital hence The orbital is $3 \mathrm{p}$.
(c) For $\mathrm{n}=4$ and $\mathrm{l}=2$ for $\mathrm{d}$ orbital hence The orbital is $4 \mathrm{~d}$.
(d) For $\mathrm{n}=4$ and $\mathrm{l}=3$ for $\mathrm{f}$ orbital hence The orbital is $4 \mathrm{f}$.
Question 29. Explain, giving reasons, which of the following sets of quantum numbers are not possible.
(a) $\mathrm{n}=0, \mathrm{l}=0, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
(b) $\quad \mathrm{n}=1, \mathrm{l}=0, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2}$
(c) $\quad \mathrm{n}=1, \mathrm{l}=1, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
(d) $\mathrm{n}=2, \mathrm{l}=0, \mathrm{~m}_{1}=1, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2}$
(e) $\quad \mathrm{n}=3, \mathrm{l}=3, \mathrm{~m}_{1}=-3, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
(f) $\quad \mathrm{n}=3, \mathrm{l}=0, \mathrm{~m}_{1}=1, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
Solution: (a) $\mathrm{n}=0, \mathrm{l}=0, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
The given set of quantum numbers is not possible because the value of the principal quantum number (n) cannot be zero. $\mathrm{n}=$
$1,1=0, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2} ;$ it is 1s orbital
The given set of quantum numbers is possible.
(b) $\mathrm{n}=1,1=1, \mathrm{~m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
For the principal quantum number (n) the value of $1=(\mathrm{n}-1)=(1-1)=0$
The given set of quantum numbers is not possible because of the value of the
azimuthal quantum number (l) cannot be equal to the principal quantum number (n)
(d) $\mathrm{n}=2, \mathrm{l}=0, \mathrm{~m}_{1}=1, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2}$
$\mathrm{n}=2, \mathrm{l}=0$ to $(\mathrm{n}-1)$ i.e. 0,1, value of $\mathrm{m}$
$=(1-1): \mathrm{m}_{1}=0, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2} \mathrm{The}$
given set of quantum numbers is not possible because the value of $\mathrm{m}$ cannot be 1
(e) $\mathrm{n}=3, \mathrm{l}=3, \mathrm{~m}_{1}=-3, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$
The given set of quantum numbers is possible. The given set of quantum numbers is not possible. For $n=3, l=0$ to $(3-1) l=0$ to 2 i.e., $0,1,2$
(f) $\mathrm{n}=3,1=0, \mathrm{~m}_{1}=1, \mathrm{~m}_{\mathrm{s}}=+\frac{1}{2}$ The given set of quantum numbers is
possible. because the value of $\mathrm{m}$ cannot be 1
Question 30. How many electrons in an atom may have the following quantum numbers?
(a) $\mathrm{n}=4, \mathrm{~m}_{\mathrm{s}}=-\frac{1}{2}$
(b) $\quad \mathrm{n}=3, \mathrm{l}=0$
Solution: (a) Formula: Total number of electrons in an atom for a value of $\mathrm{n}=2 \mathrm{n}^{2}$
$\therefore$ For $\mathrm{n}=4$
Total number of electrons $=2(4)^{2}=32$
The given element has a fully filled orbital as
$1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 4 s^{2} 3 d^{10}$
Hence, all the electrons are paired.
$\therefore$ Number of electrons (having $\mathrm{n}=4$ and $\left.\mathrm{m}_{\mathrm{s}}=-\frac{1}{2}\right)=\frac{32}{2}=16$
(b) $\mathrm{n}=3, \mathrm{l}=0$ indicates that the electrons are present in the $3 \mathrm{~s}$ orbital and $3 \mathrm{~s}$ orbital have only 2 electrons. Therefore, the number of electrons having $\mathrm{n}=3$ and $\mathrm{l}=0$ is 2
Question 31. Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
Solution: Since a hydrogen atom has only one electron, according to Bohr's postulate, the angular momentum of that electron is given by:
Formula: $\mathrm{mvr}=\mathrm{n} \frac{\mathrm{h}}{2 \pi} \ldots .(1)$
Where, $\mathrm{n}=1,2,3, \ldots$
According to de Broglie's equation:
$\lambda=\frac{\mathrm{h}}{\mathrm{mv}} \quad \frac{\mathrm{hr}}{\lambda}=\mathrm{n} \frac{\mathrm{h}}{2 \pi}$
Or
$\mathrm{mv}=\frac{\mathrm{h}}{\lambda} \ldots . .(2)$ or $2 \pi \mathrm{r}=\mathrm{n} \lambda \ldots(3)$
Since ' $2 \pi \mathrm{r}$ ' represents the circumference of the Bohr orbit (r), it is proved by equation (3) that the circumference of the Bohr orbit of the hydrogen atom is an integral multiple of de Broglie's wavelength associated with the electron revolving around the orbit.
Question 32. What transition in the hydrogen spectrum would have the same wavelength as the Balmer transition $\mathrm{n}=4$ to $\mathrm{n}=2$ of $\mathrm{He}^{+}$ spectrum?
Solution: For $\mathrm{He}^{+}$ ion, the wave number associated with the Balmer transition, $\mathrm{n}=4$ to $\mathrm{n}=2$ is given by:
$\bar{v}=\frac{1}{\lambda}=\mathrm{RZ}^{2}\left(\frac{1}{\mathrm{n}_{1}^{2}}-\frac{1}{\mathrm{n}_{2}^{2}}\right)$
Where, $\mathrm{n}_{1}=2 \mathrm{n}_{2}=4$
the atomic number of helium $(\mathrm{Z})=2$
$\bar{v}=\frac{1}{\lambda}=\mathrm{R}(2)^{2}\left(\frac{1}{4}-\frac{1}{16}\right)=4 \mathrm{R}\left(\frac{4-1}{16}\right)$
$\bar{v}=\frac{1}{\lambda}=\frac{3 R}{4}$
$\Rightarrow \lambda=\frac{4}{3 R}$
According to the question, the desired transition for hydrogen will have the same wavelength as that of $\mathrm{He}^{+}$.
$\bar{v}=\mathrm{R}(1)^{2}\left[\frac{1}{\mathrm{n}_{1}^{2}}-\frac{1}{\mathrm{n}_{2}^{2}}\right]=\frac{3 \mathrm{R}}{4}$
$\Rightarrow \mathrm{R}\left[\frac{1}{\mathrm{n}_{1}^{2}}-\frac{1}{\mathrm{n}_{2}^{2}}\right]=\frac{3 \mathrm{R}}{4} \ldots(1)$
By hit and trial method, the equality is given by equation (1) is true only when $\mathrm{n}_{1}=1$ and $\mathrm{n}_{2}=2$
The transition for $\mathrm{n}_{2}=2$ to $\mathrm{n}=1$ in hydrogen spectrum would have the same wavelength as Balmer transition $\mathrm{n}=4$ to $\mathrm{n}=2$ of $\mathrm{He}^{+}$ spectrum.
Question 33. Calculate the energy required for the process
$\mathrm{He}_{(\mathrm{g})}^{+} \rightarrow \mathrm{He}_{(\mathrm{g})}^{2+}+\mathrm{e}^{-}$
The ionization energy for the $\mathrm{H}$ atom in the ground state is $2.18 \times 10^{-18} \mathrm{~J}$ atom $^{-1}$
Solution: Energy associated with hydrogen-like species is given by,
$\mathrm{E}_{\mathrm{n}}=-2.18 \times 10^{-18}\left(\frac{\mathrm{Z}^{2}}{\mathrm{n}^{2}}\right) \mathrm{J}$
For ground state of hydrogen atom,
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{1}$
$=0-\left[-\left(2.18 \times 10^{-18} \frac{(1)^{2}}{(1)^{2}}\right] \mathrm{J}\right.$
$\Delta \mathrm{E}=2.18 \times 10^{-18} \mathrm{~J}$
For the given process,
$\mathrm{He}_{(\mathrm{g})}^{+} \rightarrow \mathrm{He}_{(\mathrm{g})}^{2+}+\mathrm{e}^{-}$
An electron is removed from $\mathrm{n}=1$ to $\mathrm{n}=\infty$.
$\Delta \mathrm{E}=\mathrm{E}_{\infty}-\mathrm{E}_{1}$
$=0-\left[-\left(2.18 \times 10^{-18} \frac{(2)^{2}}{(1)^{2}}\right] \mathrm{J}\right.$
$\Delta \mathrm{E}=8.72 \times 10^{-18} \mathrm{~J}$
$\therefore$ The energy required for the process $8.72 \times 10^{-18} \mathrm{~J}$.
Question 34. If the diameter of a carbon atom is $0.15 \mathrm{~nm}$, calculate the number of carbon atoms which can be placed side by side in a straight line across length of scale of length $20 \mathrm{~cm}$ long.
Solution: $1 \mathrm{~m}=100 \mathrm{~cm}$
$1 \mathrm{~cm}=10-2 \mathrm{~m}$
Length of the scale $=20 \mathrm{~cm}$
$=20 \times 10^{-2} \mathrm{~m}$
Diameter of a carbon atom $=0.15 \mathrm{~nm}$
$=0.15 \times 10^{-9} \mathrm{~m}$
One carbon atom occupies $0.15 \times 10^{-9} \mathrm{~m}$.
$\therefore$ Number of carbon atoms that can be placed in a straight line $\frac{20 \times 10^{-2} \mathrm{~m}}{0.15 \times 10^{-9} \mathrm{~m}}$
$=133.33 \times 10^{7}$
$=1.33 \times 10^{9}$
Question 35. $2 \times 10^{8} \mathrm{~m}$ atoms of carbon are arranged side by side. Calculate the radius of carbon atom if the length of this arrangement is $2.4 \mathrm{~cm}$.
Solution: Length of the given arrangement $=2.4 \mathrm{~cm}$
Number of carbon atoms present $=2 \times 10^{8}$
Diameter of carbon atom
$\frac{2.4 \times 10^{-2} \mathrm{~m}}{2 \times 10^{8} \mathrm{~m}} \quad \therefore$ Radius of carbon atom $=1.2 \times 10^{-10} \mathrm{~m}$
$=\frac{\text { Diameter }}{2}$
$=\frac{1.2 \times 10^{-10} \mathrm{~m}}{2}$
$=6.0 \times 10^{-11} \mathrm{~m}$
Question 36. The diameter of zinc atom is 2.6 Å.Calculate
(a) Radius of zinc atom in pm and
(b) Number of atoms present in a length of $1.6 \mathrm{~cm}$ if the zinc atoms are arranged side by side lengthwise.
Solution: (a) Formula: Radius of carbon atom $=\frac{\text { Diameter }}{2}$
$=\frac{2.6}{2}$
$=1.3 \times 10^{-10} \mathrm{~m}$
$=130 \times 10^{-12} \mathrm{~m}$
$=130 \mathrm{pm}$
(b) Length of the arrangement $=1.6 \mathrm{~cm}$
$=1.6 \times 10^{-2} \mathrm{~m}$
Diameter of zinc atom $=1.6 \times 10^{-10} \mathrm{~m}$
$\therefore$ Number of zinc atoms present in the arrangement
$=1 \cdot \frac{6 \times 10^{-2} \mathrm{~m}}{2.6 \times 10^{-10} \mathrm{~m}}$
$=0.6153 \times 10^{8} \mathrm{~m}$
$=6.153 \times 10^{7} \mathrm{~m}$
Question 37. The diameter of zinc atom is 2.6 Å. Calculate
(a) radius of zinc atom in pm and
(b) number of atoms present in a length of $1.6 \mathrm{~cm}$ if the zinc atoms are arranged side by side lengthwise.
Solution: (a) Radius of carbon atom $=\frac{\text { Diameter }}{2}$
$=\frac{2.6}{2}$
$=1.3 \times 10^{-10} \mathrm{~m}$
$=130 \times 10^{-12} \mathrm{~m}$
$=130 \mathrm{pm}$
(b) Length of the arrangement $=1.6 \mathrm{~cm}$
$=1.6 \times 10^{-2} \mathrm{~m}$
Diameter of zinc atom $=1.6 \times 10^{-10} \mathrm{~m}$
Therefore, Number of zinc atoms present in the arrangement
$=\frac{1.6 \times 10^{-2} \mathrm{~m}}{2.6 \times 10^{-10} \mathrm{~m}}$
$=0.6153 \times 10^{8} \mathrm{~m}$
$=6.153 \times 10^{7} \mathrm{~m}$
Question 38. A certain particle carries $2.5 \times 10^{-16} \mathrm{C}$ of static electric charge. Calculate the number of electrons present in it.
Solution: Charge on one electron $=1.6022 \times 10^{-19} \mathrm{C}$
$\Rightarrow 1.6022 \times 10^{-19} \mathrm{C}$ charge is carried by 1 electron.
Therefore, Number of electrons carrying a charge of
$2.5 \times 10^{-16} \mathrm{C} \frac{1}{1.6022 \times 10^{-19} \mathrm{C}}\left(2.5 \times 10^{-16} \mathrm{C}\right)$
$=1.560 \times 10^{3} \mathrm{C}$
$=1560 \mathrm{C}$
Question 39. In Milikan's experiment, static electric charge on the oil drops has been obtained by shining X-rays. If the static electric charge on the oil drop is $-1.282 \times$ $10^{-18} \mathrm{C}$, calculate the number of electrons present on it.
Solution: Charge on the oil drop $=1.282 \times 10^{-18} \mathrm{C}$
Charge on one electron $=1.6022 \times 10^{-19} \mathrm{C}$
Therefore, Number of electrons present on the oil drop
$\frac{1.282 \times 10^{-18} \mathrm{C}}{1.6022 \times 10^{-19} \mathrm{C}}$
$=0.8001 \times 10^{1}$
$=8.0$
Question 40. In Rutherford's experiment, generally the thin foil of heavy atoms, like gold, platinum etc. have been used to be bombarded by the $\alpha$ -particles. If the thin foil of light atoms like Aluminium etc. is used, what difference would be observed from the above results?
Solution: A thin foil of lighter atoms will not give the same results as given with the foil of heavier atoms.
Lighter atoms would be able to carry very little positive charge. Hence, they will not cause enough deflection of $\alpha$ -particles (positively charged).
Question 41. Symbols ${ }_{35}^{79} \mathrm{Br}$ and ${ }^{79} \mathrm{Br}$ can be written, whereas symbols ${ }_{79}^{35} \mathrm{Br}$ and ${ }^{35} \mathrm{Br}$ are not acceptable. Answer briefly.
Solution: The general convention of representing an element along with its atomic mass (A) and atomic number (Z) is ${ }_{\mathrm{Z}}^{\mathrm{A}} \mathrm{X}$.
Hence, ${ }_{35}^{79} \mathrm{Br}$ is acceptable but ${ }_{79}^{35} \mathrm{Br}$ is not acceptable.
${ }^{79} \mathrm{Br}$ can be written but ${ }^{35} \mathrm{Br}$ cannot be written because the atomic number of an element is constant, but the atomic mass of an element depends upon the relative abundance of its isotopes. Hence, it is necessary to mention the atomic mass of an element.
Question 42. An element with mass number 81 contains $31.7 \%$ more neutrons as compared to protons. Assign the atomic symbol.
Solution: Let the number of protons in the element be $\mathrm{x}$.
Therefore, Number of neutrons in the element $=\mathrm{x}+31.7 \%$ of $\mathrm{x}$
$=\mathrm{x}+0.317 \mathrm{x}$
$=1.317 \mathrm{x}$
According to the question,
Mass number of the element $=81$
Therefore, (Number of protons $+$ number of neutrons $)=81$
$\Rightarrow x+1.317 x=81 \simeq 35$
$2.317 x=81 x$
$=\frac{81}{2.317}$
$=34.95 \cong 35$
Hence, the number of protons in the element i.e., $\mathrm{x}$ is 35 .
Since the atomic number of an atom is defined as the number of protons present in its nucleus, the atomic number of the given element is 35 .
Therefore, the atomic symbol of the element is ${ }_{35}^{81} \mathrm{Br}$
Question 43. An ion with mass number 37 possesses one unit of negative charge. If the ion contains $11.1 \%$ more neutrons than the electrons, find the symbol of the ion.
Solution: Let the number of electrons in the ion carrying a negative charge be $\mathrm{x}$.
$=\mathrm{x}+0.111 \mathrm{x}$
$=1.111 \mathrm{x}$
Number of electrons in the neutral atom $=(\mathrm{x}-1)$
(When an ion carries a negative charge, it carries an extra electron)
Therefore, Number of protons in the neutral atom $=\mathrm{x}-1$
Given,
Mass number of the ion $=37$
Therefore, $(\mathrm{x}-1)+1.111 \mathrm{x}=37$
$2.111 x=38 x$
$=18$
Therefore, The symbol of the ion is ${ }_{17}^{37} \mathrm{Cl}^{-}$
Question 44. An ion with mass number 56 contains 3 units of positive charge and $30.4 \%$ more neutrons than electrons. Assign the symbol to this ion.
Solution: Let the number of electrons present in ion $A^{3+}$ be $x$.
Therefore, Number of neutrons in $\mathrm{it}=x+30.4 \%$ of $x=1.304 x$
Since the ion is tripositive,
$\Rightarrow$ Number of electrons in neutral atom $=x+3$
Therefore, Number of protons in neutral atom $=x+3$
Given: Mass number of the ion $=56$
Therefore, $(x+3)(1.304 x)=56$
$2.304 x=53$
$x=532.304$
$x=23$
Therefore, Number of protons $=x+3=23+3=26$
Therefore, The symbol of the ion $\frac{56}{26} \mathrm{Fe}^{+}$
Question 45. Arrange the following type of radiations in increasing order of frequency:
(a) radiation from microwave oven
(b) amber light from traffic signal
(c) radiation from FM radio
(d) cosmic rays from outer space and
(e) X-rays.
Solution: The increasing order of frequency is as follows:
Radiation from FM radio $<$ amber light $<$ radiation from microwave oven $<\mathrm{X}-$ rays $<$ cosmic rays
The increasing order of wavelength is as follows:
Cosmic rays $
Question 46. Nitrogen laser produces a radiation at a wavelength of $337.1 \mathrm{~nm}$. If the number of photons emitted is $5.6 \times 1024$, calculate the power of this laser.
Solution: Power of laser $=$ Energy with which it emits photons
Formula: Power $=\mathrm{E}=$ Nhc $\lambda$
Where, $\mathrm{N}=$ number of photons emitted
$\mathrm{h}=$ Planck's constant
$\mathrm{c}=$ velocity of radiation
$\lambda=$ wavelength of radiation
Substituting the values in the given expression of Energy (E):
$E=\frac{\left(5.6 \times 10^{24}\right)(6.62 \times 10-34 \mathrm{Js})\left(3 \times 10^{8} \mathrm{~ms}-1\right)}{337.1 \times 10^{-9} \mathrm{~m}}$
$=0.3302 \times 10^{7} \mathrm{~J}$
$=3.33 \times 10^{6} \mathrm{~J}$
Hence, the power of the laser is $3.33 \times 10^{6} \mathrm{~J}$
Question 47. Neon gas is generally used in the sign boards. If it emits strongly at $616 \mathrm{~nm}$, calculate
(a) the frequency of emission,
(b) distance traveled by this radiation in $30 \mathrm{~s}$
(c) energy of quantum and
(d) number of quanta present if it produces $2 \mathrm{~J}$ of energy.
Solution: Wavelength of radiation emitted $=616 \mathrm{~nm}=616 \times 10^{-9} \mathrm{~m}$ (Given)
(a) Frequency of emission (v)
$v=c \lambda$
Where, $\mathrm{c}=$ velocity of radiation
$\lambda=$ wavelength of radiation
Substituting the values in the given expression of $(v)$ :
$v=3 \times \frac{108 \mathrm{~m}}{\mathrm{~s} 616} \times 10^{-9} \mathrm{~m}$
$=4.87 \times 10^{8} \times 10^{9} \times 10^{-3} \mathrm{~s}^{-1}$
$\mathrm{v}=4.87 \times 10^{14} \mathrm{~s}^{-1}$
Frequency of emission $(v)=4.87 \times 10^{14} \mathrm{~s}^{-1}$
(b) We know: Velocity of radiation, $\mathrm{c}=3 \times 10^{8} \mathrm{~ms}^{-1}$
Distance travelled by this radiation in $30 \mathrm{~s}$
$=\left(3 \times 10^{8} \mathrm{~ms}^{-1}\right)(30 \mathrm{~s})$
$=9 \times 10^{9} \mathrm{~m}$
(c) Energy of quantum $(\mathrm{E})=\mathrm{h} v$
$=\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(4.87 \times 10^{14} \mathrm{~s}^{-1}\right)$
Energy of quantum $(\mathrm{E})=32.27 \times 10^{-20} \mathrm{~J}$
Therefore, $32.27 \times 10^{-20} \mathrm{~J}$ of energy is present in 1 quantum.
Number of quanta in $2 \mathrm{~J}$ of energy
$\frac{2 \mathrm{~J}}{32.27 \times 10^{-20} \mathrm{~J}}=6.19 \times 10^{18}=6.2 \times 10^{18}$
Question 48. In astronomical observations, signals observed from the distant stars are generally weak. If the photon detector receives a total of $3.15 \times 10^{-18} \mathrm{~J}$ from the radiations of $600 \mathrm{~nm}$, calculate the number of photons received by the detector.
Solution: We know: velocity of radiation (c) $=3 \times 10^{8} \mathrm{~ms}^{-1}$
Planck's constant $(\mathrm{h})=6.62 \times 10^{-34} \mathrm{Js}$
Given: Wavelength $(\lambda)=600 \mathrm{~nm}$
Energy received by the photons $=3.15 \times 10^{-18} \mathrm{~J}$
From the expression of energy of one photon (E),
Formula: $\mathrm{E}=$ hc $\lambda$
Where,
$\lambda=$ wavelength of radiation
$\mathrm{h}=$ Planck's constant
$\mathrm{c}=$ velocity of radiation
Substituting the values in the given expression of $\mathrm{E}$ :
$E=\frac{\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(3 \times 10^{8} \mathrm{~ms}^{-1}\right)}{600 \times 10^{-9}}=3.313 \times 10^{-19} \mathrm{~J}$
Energy of one photon $=3.313 \times 10^{-19} \mathrm{~J}$
Number of photons received with $3.15 \times 10^{-18} \mathrm{~J}$ of energy
$=\frac{3.15 \times 10^{-18} \mathrm{~J}}{3.313 \times 10^{-19} \mathrm{~J}}$
$=9.5 \approx 10$
Question 49. Lifetimes of the molecules in the excited states are often measured by using pulsed radiation source of duration nearly in the nano second range. If the radiation source has the duration of $2 \mathrm{~ns}$ and the number of photons emitted during the pulse source is $2.5 \times 10^{15} \mathrm{~J}$, calculate the energy of the source.
Solution: Frequency of radiation (v),
$v=12.0 \times 10^{-9} \mathrm{~s}$
$v=5.0 \times 10^{8} \mathrm{~s}^{-1}$
Energy (e) $\quad$ of source $=\mathrm{Nhv}$
Where,
$\mathrm{N}=$ number of photons emitted
$\mathrm{h}=$ Planck's constant
$v=$ frequency of radiation
Substituting the values in the given expression of (E):
$\mathrm{E}=\left(2.5 \times 10^{15}\right)\left(6.62 \times 10^{-34} \mathrm{Js}\right)(5.0 \times 108 \mathrm{~s}-1)$
$\mathrm{E}=8.282 \times 10^{-10} \mathrm{~J}$
Hence, the energy of the source (e) is $8.282 \times 10^{-10} \mathrm{~J}$.
Question 50. The work function for cesium atom is $1.9 \mathrm{eV}$. Calculate
(a) the threshold wavelength and
(b) the threshold frequency of the radiation. If the cesium element is irradiated with a wavelength $500 \mathrm{~nm}$, calculate the kinetic energy and the velocity of the ejected photoelectron.
Solution: It is given that the work function $\left(\mathrm{W}_{0}\right)$ for cesium atom is $1.9 \mathrm{eV}$.
(a) From the $\mathrm{W}_{0}=\mathrm{hc} \lambda_{0}$ expression, we get:
$\lambda_{0}=\mathrm{hcW}_{0}$
Where,
$\lambda_{0}=$ threshold wavelength
$\mathrm{h}=$ Planck's constant
$c=$ velocity of radiation
Substituting the values in the given expression of $\left(\lambda_{0}\right):$
$\lambda_{0}=\frac{\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(3 \times 10^{8} \mathrm{~ms}^{-1}\right)}{\left(1.9 \times 1.602 \times 10^{-19} \mathrm{~J}\right)}$
$=6.53 \times 10^{-7} \mathrm{~m}$
Hence, the threshold wavelength $\left(\lambda_{0}\right)$ is $653 \mathrm{~nm}$.
(b) Formula: From the expression, $W_{0}=h v_{0}$, we get:
$v_{0}=W_{0} h$
Where,
$v_{0}=$ threshold frequency
$\mathrm{h}=$ Planck's constant
Substituting the values in the given expression of $v_{0}$ :
$v_{0}=\frac{1.9 \times 1.602 \times 10^{-19} \mathrm{~J}}{6.62 \times 10^{-34} \mathrm{Js}}$
(i e., $\left.V=1.602 \times 10^{-19} \mathrm{~J}\right)$
$v_{0}=4.593 \times 10^{14} \mathrm{~s}^{-1}$
Hence, the threshold frequency of radiation $\left(v_{0}\right)$ is $4.593 \times 10^{14} \mathrm{~s}^{-1}$
(c) According to the question:
Wavelength used in irradiation $(\lambda)=500 \mathrm{~nm}$
Formula: Kinetic energy $=\mathrm{h}(v-v 0)$
$=\mathrm{hc}\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)$
$=\left(6.62 \times 10^{-34} \mathrm{Js}\right)(3.0 \times 108 \mathrm{~ms}-1)\left(\frac{\lambda_{0}-\lambda}{\lambda \lambda_{0}}\right)$
$=\left(1.9878 \times 10^{-26} \mathrm{Jm}\right)\left[\frac{(653-500) 10^{-9} \mathrm{~m}}{(653)(500) 10^{-18} \mathrm{~m}^{2}}\right]$
$=\frac{\left(1.9878 \times 10^{-26}\right)\left(153 \times 10^{9}\right)}{(653)(500) \mathrm{J}}=9.3149 \times 10^{-20} \mathrm{~J}$
Kinetic energy of the ejected photoelectron $=9.3149 \times 10^{-20} \mathrm{~J}$
Since K. E = $\frac{1}{2} \mathrm{mv}^{2}=9.3149 \times 10^{-20} \mathrm{~J}$
$v=\sqrt{\frac{2\left(9.3149 \times 10^{-20} \mathrm{~J}\right)}{9.10939 \times 10-31}}$
$=\sqrt{2.0451 \times 10^{11} \mathrm{~m}^{2} \mathrm{~s}^{2}}$
$=4.52 \times 10^{5} \mathrm{~ms}^{-1}$
Question 51. Following results are observed when sodium metal is irradiated with different wavelengths. Calculate
(a) Threshold wavelength and,
(b) Planck's constant.
Solution: (a) Assuming the threshold wavelength to be $\lambda_{0} \mathrm{~nm}\left(=\lambda_{0} \times 10^{-} 9 \mathrm{~m}\right)$, the kinetic energy of the radiation is given as:
$\mathrm{h}\left(v-v_{0}\right)=\frac{1}{2} \mathrm{mv}^{2}$
Three different equalities can be formed by the given value as:
$\mathrm{h}\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)=\frac{1}{2} \mathrm{mv}^{2}$
$h c\left(\frac{1}{500 \times 10^{9}}-\frac{1}{\lambda_{0} \times 10-9 m}\right)$
$=\frac{1}{2} m\left(2.55 \times 10^{+5} \times 10^{-2} \mathrm{~ms}^{-1}\right)$
$\frac{h c}{10^{-9} m}\left(\frac{1}{500}-\frac{1}{\lambda_{0}}\right)=12 m\left(2.55 \times 10^{+3} m s^{-1}\right)^{2}$(1)
Similarly,
$\frac{h c}{10^{-9} m}\left(\frac{1}{450}-\frac{1}{\lambda_{0}}\right)=\frac{1}{2 m}$
$\left(3.45 \times 10^{+3} \mathrm{~ms}^{-1}\right)^{2}$(2)
$\frac{h c}{10^{-9} m}\left(\frac{1}{400}-\frac{1}{\lambda_{0}}\right)=\frac{1}{2 m}$
$\left(5.35 \times 10^{+3} \mathrm{~ms}^{-1}\right)^{2}$(3)
Dividing equation (3) by equation (1):
$\frac{\left[\frac{\lambda_{0}-400}{400 \lambda_{0}}\right]}{\left[\frac{\lambda_{0}-500}{500 \lambda_{0}}\right]}=\frac{\left(5.35 \mid \times 10^{+3} \mathrm{~ms}^{-1}\right)^{2}}{\left(2.55 \mid \times 10^{+3} \mathrm{~ms}^{-1}\right)^{2}}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=\frac{(5.35)^{2}}{(2.55)^{2}}=\frac{28.6225}{6.5025}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=4.40177$
$17.6070 \lambda_{0}-5 \lambda_{0}=8803.537-2000$
$\lambda_{0}=\frac{6805.537}{12.607}$
$\lambda_{0}=539.8 \mathrm{~nm}$
$\lambda_{0}=540 \mathrm{~nm}$
So, threshold wavelength $\left(\lambda_{0}\right)=540 \mathrm{~nm}$
(b) of the question is not done due to the incorrect values of velocity given in the question.
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=(5.35)^{2}(2.55)^{2}$
$=\frac{28.6225}{6.5025}$
$\frac{5 \lambda_{0}-2000}{4 \lambda 0-2000}=4.40177$
$17.6070 \lambda_{0}-5 \lambda_{0}=8803.537-2000$
$\lambda_{0}=\frac{6805.537}{12.607}$
$\lambda_{0}=539.8 \mathrm{~nm}$
$\lambda_{0}=540$
Question 52. The ejection of the photoelectron from the silver metal in the photoelectric effect experiment can be stopped by applying the voltage of $0.35 \mathrm{~V}$ when the radiation $256.7 \mathrm{~nm}$ is used. Calculate the work function for silver metal.
Solution: Given: Stopping potential $=0.35 \mathrm{~V}$
Wavelength of radiation $=256.7 \mathrm{~nm}$
We know: velocity of radiation $(\mathrm{c})=3 \times 10^{8} \mathrm{~ms}^{-1}$
Planck's constant $(\mathrm{h})=6.62 \times 10^{-34} \mathrm{Js}$
From the principle of conservation of energy, the energy of an incident photon (e) is equal to the sum of the work function $\left(\mathrm{W}_{0}\right)$ of radiation and its kinetic energy (K.E) i.e.,
Fomula: $E=W_{0}+K . E$
$\Rightarrow \mathrm{W}_{0}=\mathrm{E}-\mathrm{K} . \mathrm{E}$
Formula: Energy of incident photon $(\mathrm{E})=\frac{\mathrm{hc}}{\lambda}$
Where,
$\mathrm{c}=$ velocity of radiation
$\mathrm{h}=$ Planck's constant
$\lambda=$ wavelength of radiation
Substituting the values in the given expression of $E$ :
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34} \mathrm{Js}\right)\left(3 \times 10^{8} \mathrm{~ms}^{-1}\right)}{\left(256.7 \times 10^{-9} \mathrm{~m}\right)}$
$=7.744 \times 10^{-19} \mathrm{~J}$
$=\frac{7.744 \times 10^{-19}}{1.602 \times 10^{-19}} \mathrm{eV}$
$\mathrm{E}=4.83 \mathrm{eV}$
The potential applied to silver metal changes to kinetic energy (K.E) of the photoelectron.
Hence,
$\mathrm{K} . \mathrm{E}=0.35 \mathrm{~V}$
$\mathrm{K} . \mathrm{E}=0.35 \mathrm{eV}$
Therefore, Work function, $\mathrm{W}_{0}=\mathrm{E}-\mathrm{K} . \mathrm{E} \quad[$ Formula $]$
$=4.83 \mathrm{eV}-0.35 \mathrm{eV}$
$=4.48 \mathrm{eV}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=\frac{(5.35)^{2}}{(2.55)^{2}}=\frac{28.6225}{6.5025}$
$5 \lambda_{0}-20004 \lambda_{0}-2000=4.40177$
$17.6070 \lambda_{0}-5 \lambda_{0}=8803.537-2000$
$\lambda_{0}=\frac{6805.537}{12.607}$
$\lambda_{0}=539.8 \mathrm{~nm}$
$\lambda_{0} \simeq 540 \mathrm{~nm}$
Question 53. If the photon of the wavelength $150 \mathrm{pm}$ strikes an atom and one of its inner bound electrons is ejected out with a velocity of $1.5 \times 10^{7} \mathrm{~ms}^{-1}$, calculate the energy with which it is bound to the nucleus.
Solution: Given: Wavelength of photon $=150 \mathrm{pm}$
Velocity of ejected electrons $=1.5 \times 10^{7} \mathrm{~ms}^{-1}$
We know: velocity of radiation $(\mathrm{c})=3 \times 10^{8} \mathrm{~ms}^{-1}$
Planck's constant $(\mathrm{h})=6.62 \times 10^{-34} \mathrm{Js}$
Formula: Energy of incident photon (E)is given by,
$\mathrm{E}=\frac{\mathrm{hc}}{\lambda}$
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(150 \times 10^{-12}\right)}$
$=1.3252 \times 10^{-15} \mathrm{~J}$
$\simeq 13.252 \times 10^{-16} \mathrm{~J}$
Energy of the electron ejected $(\mathrm{K} . \mathrm{E})=\frac{1}{2} \mathrm{~m}_{\mathrm{e}} v^{2}$
$=12\left(9.10939 \times 10^{-31} \mathrm{~kg}\right)$
$\left(1.5 \times 10^{7} \mathrm{~ms}^{-1}\right)^{2}$
$=10.2480 \times 10^{-17} \mathrm{~J}$
$=1.025 \times 10^{-16} \mathrm{~J}$
Hence, the energy with which the electron is bound to the nucleus can be obtained as:
$=\mathrm{E}-\mathrm{K} . \mathrm{E}$
$=13.252 \times 10^{-16} \mathrm{~J}-1.025 \times 10^{-16} \mathrm{~J}$
$=12.227 \times 10^{-16} \mathrm{~J}$
$=\frac{12.227 \times 10^{-16}}{1.602 \times 10^{-19}} \mathrm{eV}$
$=7.6 \times 10^{3} \mathrm{eV}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=\frac{(5.35)^{2}}{(2.55)^{2}}=\frac{28.6225}{6.5025}$
$\frac{5 \lambda_{0}-2000}{4 \lambda_{0}-2000}=4.40177$
$17.6070 \lambda_{0}-5 \lambda_{0}=8803.537-2000$
$\lambda_{0}=\frac{6805.537}{12.607}$
$\lambda_{0}=539.8 \mathrm{~nm}$
$\lambda_{0} \simeq 540 \mathrm{~nm}$
Question 54. Emission transitions in the Paschen series end at orbit $\mathrm{n}=3$ and start from orbit $\mathrm{n}$ and can be represented as $\mathrm{v}=3.29 \times 10^{15} \mathrm{~Hz}\left[\frac{1}{3^{2}}-\frac{1}{\mathrm{n}^{2}}\right]$ Calculate the value of $\mathrm{n}$ if the transition is observed at $1285 \mathrm{~nm}$. Find the region of the spectrum.
Solution: Given: Wavelength of transition $=1285 \mathrm{~nm}$
$=1285 \times 10^{-9} \mathrm{~m}$
$v=3.29 \times 10^{15}\left(\frac{1}{3^{2}}-\frac{1}{n^{2}}\right)$
Formula: Since $v=\frac{c}{\lambda}$
$=\frac{3 \times 10^{8} \mathrm{~ms}^{-1}}{1285 \times 10-9 \mathrm{~m}}$
Now, $v=2.33 \times 10^{14} \mathrm{~s}^{-1}$
Substituting the value of $v$ in the given expression,
$3.29 \times 10^{15}\left(\frac{1}{9}-\frac{1}{\mathrm{n}^{2}}\right)=2.33 \times 10^{14}$
$\frac{1}{9}-\frac{1}{n^{2}}=\frac{2.33 \times 10^{14}}{3.29 \times 10^{15}}$
$\frac{1}{9}-0.7082 \times 10^{-1}=\frac{1}{n^{2}}$
$\Rightarrow \frac{1}{\mathrm{n}^{2}}=1.1 \times 10^{-1}-0.7082 \times 10^{-1}$
$\frac{1}{n^{2}}=4.029 \times 10^{-2} n$
$=14.029 \times 10^{-2}$
$\mathrm{n}=4.98$
$n=5$
Hence, for the transition to be observed at $1285 \mathrm{~nm}, \mathrm{n}=5$. The spectrum lies in the infra-red region.
Question 55. Calculate the wavelength for the emission transition if it starts from the orbit having radius $1.3225 \mathrm{~nm}$ and ends at $211.6 \mathrm{pm}$. Name the series to which this transition belongs and the region of the spectrum.
Solution: Radius of the initial orbit $=1.3225 \mathrm{~nm}$
Radius of the final orbit $=211.6 \mathrm{pm}$
Formula: The radius of the $\mathrm{n}$ th orbit of hydrogen-like particles is given by,
$r=\frac{0.529 n^{2}}{Z} Å$
$\mathrm{r}=\frac{5.29 \mathrm{n}^{2}}{\mathrm{Z}} \mathrm{pm}$
For radius $\left(r_{1}\right)=1.3225 \mathrm{~nm}$
$=1.32225 \times 10^{-9} \mathrm{~m} \mathrm{n}_{1}^{2}=\frac{\mathrm{r}_{1} \mathrm{z}}{52.9}$
$=1322.25 \times 10^{-12} \mathrm{~m} \mathrm{n}_{1}^{2}=\frac{1322.25 \mathrm{Z}}{52.9}$
$=1322.25 \mathrm{pm}$
Similarly,
$\mathrm{n}_{2}^{2}=\frac{211.6 \mathrm{Z}}{52.9}$
$\frac{\mathrm{n}_{1}^{2}}{\mathrm{n}_{2}^{2}}=\frac{1322.5}{211.6}$
$\frac{\mathrm{n}_{1}^{2}}{\mathrm{n}_{2}^{2}}=6.25$
$\frac{\mathrm{n}^{1}}{\mathrm{n}^{2}}=2.5$
$\frac{\mathrm{n}^{1}}{\mathrm{n}^{2}}=\frac{25}{10}=\frac{5}{2}$
$\Rightarrow \mathrm{n} 1=5$ and $\mathrm{n} 2=2$ Thus, the transition is from the 5 th orbit to the 2 nd orbit. It belongs to the Balmer series. wave number $(\bar{v})$ for the transition is given by,
$1.097 \times 10^{7}\left(\frac{1}{2^{2}}-\frac{1}{5^{2}}\right) \mathrm{m}^{-1}$
$=1.097 \times 10^{7} \mathrm{~m}^{-1}\left(\frac{21}{100}\right)$
$=2.303 \times 10^{6} \mathrm{~m}^{-1}$
Wavelength $(\lambda)$ associated with the emission transition is given by,
$\lambda=1 v$
$=12.303 \times 10^{6} \mathrm{~m}^{-1}$
$=0.434 \times 10^{-6} \mathrm{~m} \lambda$
$=434 \mathrm{~nm}$
Question 56. Dual behavior of matter proposed by de Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules and other type of material. If the velocity of the electron in this microscope is $1.6 \times 10^{6} \mathrm{~ms}^{-1}$, calculate de Broglie wavelength associated with this electron.
Solution: Given: velocity of the electron $=1.6 \times 10^{6} \mathrm{~ms}^{-1}$
We know: Mass of electron $=9.103939 \times 10^{-31} \mathrm{~kg}$
Formula: From de Broglie's equation,
$\lambda=\frac{\mathrm{h}}{\mathrm{m} v}$
$=\frac{\left(6.62 \times 10^{-34}\right)}{9.103939 \times 10^{-31} \mathrm{~kg}\left(1.6 \times 10^{6} \mathrm{~ms}^{-1}\right)}$
$=4.55 \times 10^{-10} \mathrm{~m} \lambda=455 \mathrm{pm}$
de Broglie's wavelength associated with the electron is $455 \mathrm{pm}$.
Question 57. Similar to electron diffraction, neutron diffraction microscope is also used for the determination of the structure of molecules. If the wavelength used here is $800 \mathrm{pm}$, calculate the characteristic velocity associated with the neutron.
Solution: Given: The wavelength used $=800 \mathrm{pm}$
We know: Planck's constant $=6.62 \times 10^{-34}$
Mass of the particle $=1.67 \times 10^{-27} \mathrm{~kg}$
From de Broglie's equation,
$\lambda=\frac{\mathrm{h}}{\mathrm{mv}}$
$v=\frac{h}{m \lambda}$
Where,
$\mathrm{v}=$ velocity of particle (neutron)
$\mathrm{h}=$ Planck's constant
$\mathrm{m}=$ mass of particle (neutron)
$\lambda=$ wavelength
Substituting the values in the expression of velocity (v),
$\mathrm{E}=\frac{\left(6.62 \times 10^{-34}\right)}{\left(1.67 \times 10^{-27}\right)\left(800 \times 10^{-12} \mathrm{~m}\right)}$
$=4.94 \times 10^{2} \mathrm{~J}$
$=494 \mathrm{~ms}^{-1}$
Velocity associated with the neutron $=494 \mathrm{~ms}^{-1}$
Question 58. If the velocity of the electron in Bohr's first orbit is $2.19 \times 10^{6} \mathrm{~ms}^{-1}$, calculate the de Broglie wavelength associated with it.
Solution:
Given: velocity of the electron in first orbit $=2.19 \times 10^{6} \mathrm{~ms}^{-1}$
We know: The value of planck's constant $=6.62 \times 10^{-34}$
Formula: According to de Broglie's equation,
$\lambda=\frac{\mathrm{h}}{\mathrm{mv}}$
Where, $\lambda=$ wavelength associated with the electron
$\mathrm{h}=$ Planck's constant
$\mathrm{m}=$ mass of electron
$\mathrm{v}=$ velocity of electron Substituting the values in the expression of $\lambda$ :
$\lambda=\frac{h}{m v}$
$=\frac{\left(6.62 \times 10^{-34}\right)}{9.103939 \times 10^{-31} \mathrm{~kg}\left(2.19 \times 10^{6} \mathrm{~ms}^{-1}\right)}$
$=3.32 \times 10^{-10} \mathrm{~m} \lambda=332 \mathrm{pm}$
Question 59. The velocity associated with a proton moving in a potential difference of $1000 \mathrm{~V}$ is $4.37 \times 10^{5} \mathrm{~ms}^{-1}$. If the hockey ball of mass $0.1 \mathrm{~kg}$ is moving with this velocity, calculate the wavelength associated with this velocity.
Solution: Given: Potential difference $=1000 \mathrm{~V}$
Velocity of the proton $=4.37 \times 10^{5} \mathrm{~ms}^{-1}$
Mass of the hockey ball $=0.1 \mathrm{~kg}$
We know: Planck's constant $(\mathrm{h})=6.62 \times 10^{-34}$
Formula: According to de Broglie's expression,
$\lambda=\frac{\mathrm{h}}{\mathrm{m} v}$
$=\frac{\left(6.62 \times 10^{-34}\right)}{0.1 \mathrm{~kg}\left(4.37 \times 10^{5} \mathrm{~ms}^{-1}\right)}$
$=1.516 \times 10^{-38} \mathrm{~m}$
Question 60. If the position of the electron is measured within an accuracy of $+0.002 \mathrm{~nm}$, calculate the uncertainty in the momentum of the electron. Suppose the momentum of the electron is $\mathrm{h} / 4 \pi_{\mathrm{m}} \times 0.05 \mathrm{~nm}$, is there any problem in defining this value.
Solution: Given: Accuracy in measurement of position $=+0.002 \mathrm{~nm}$
Momentum of the electron $=\frac{\mathrm{h}}{4 \pi_{\mathrm{m}}} \times 0.05 \mathrm{~nm}$
From Heisenberg's uncertainty principle,
Where,
$\Delta \mathrm{x}=$ uncertainty in position of the electron
$\Delta \mathrm{p}=$ uncertainty in momentum of the electron
Substituting the values in the expression of $\Delta \mathrm{p}$ :
$=2.637 \times 10^{-23} \mathrm{Jsm}^{-1}$
$\Delta \mathrm{p}=2.637 \times 10^{-23} \mathrm{kgms}^{-1}\left(1 \mathrm{~J}=1 \mathrm{kgms} 2 \mathrm{~s}^{-1}\right)$
Uncertainty in the momentum of the electron $=2.637 \times 10^{-23} \mathrm{kgms}^{-1} .=$ $1.055 \times 10^{-24} \mathrm{kgms}^{-1}$
Since the magnitude of the actual momentum is smaller than the uncertainty, the value cannot be defined.
Question 61. The quantum numbers of six electrons are given below. Arrange them in order of increasing energies. If any of these combination (s) has/have the same energy lists:
1. $\mathrm{n}=4, \mathrm{l}=2, \mathrm{ml}=-2, \mathrm{~m}_{\mathrm{s}}=-1 / 2$
2. $\mathrm{n}=3, \mathrm{l}=2, \mathrm{ml}=1, \mathrm{~m}_{\mathrm{s}}=+1 / 2$
3. $\mathrm{n}=4, \mathrm{l}=1, \mathrm{ml}=0, \mathrm{~m}_{\mathrm{s}}=+1 / 2$
4. $\mathrm{n}=3, \mathrm{l}=2, \mathrm{ml}=-2, \mathrm{~m}_{\mathrm{s}}=-1 / 2$
5. $\mathrm{n}=3, \mathrm{l}=1, \mathrm{ml}=-1, \mathrm{~m}_{\mathrm{s}}=+1 / 2$
6. $\mathrm{n}=4, \mathrm{l}=1, \mathrm{ml}=0, \mathrm{~m}_{\mathrm{s}}=+1 / 2$
Solution: For $\mathrm{n}=4$ and $\mathrm{l}=2$, the orbital occupied is $4 \mathrm{~d}$.
For $\mathrm{n}=3$ and $\mathrm{l}=2$, the orbital occupied is $3 \mathrm{~d}$.
For $\mathrm{n}=4$ and $\mathrm{l}=1$, the orbital occupied is $4 \mathrm{p}$.
Hence, the six electrons i.e., $1,2,3,4,5$, and 6 are present in the $4 \mathrm{~d}, 3 \mathrm{~d}, 4 \mathrm{p}, 3 \mathrm{~d}, 3 \mathrm{p}$, and $4 \mathrm{p}$ orbitals respectively.
Therefore, the increasing order of energies is $5(3 p)<2(3 d)=4(3 \mathrm{~d})<$ $3(4 p)=6(4 p)<1(4 d)$
Question 62. The bromine atom possesses 35 electrons. It contains 6 electrons in $2 \mathrm{p}$ orbital, 6 electrons in $3 \mathrm{p}$ orbital and 5 electrons in $4 \mathrm{p}$ orbital. Which of these electron experiences the lowest effective nuclear charge?
Solution: Nuclear charge experienced by an electron (present in a multi-electron atom) is dependant upon the distance between the nucleus and the orbital, in which the electron is present. As the distance increases, the effective nuclear charge also decreases. Among p-orbitals, $4 \mathrm{p}$ orbitals are farthest from the nucleus of bromine atom with $(+35)$ charge. Hence, the electrons in the $4 \mathrm{p}$ orbital will experience the lowest effective nuclear charge. These electrons are shielded by electrons present in the $2 \mathrm{p}$ and $3 \mathrm{p}$ orbitals along with the s-orbitals. Therefore, they will experience the lowest nuclear charge.
Question 63. Among the following pairs of orbitals which orbital will experience the larger effective nuclear charge?
(i) $\quad 2$ s and $3 s$,
(ii) $4 \mathrm{~d}$ and $4 \mathrm{f}$,
(iii) $3 \mathrm{~d}$ and $3 \mathrm{p}$
Solution: Nuclear charge is defined as the net positive charge experienced by an electron in the orbital of a multi-electron atom. The closer the orbital, the greater is the nuclear charge experienced by the electron $(\mathrm{s})$ in it.
(i) The electron(s) present in the $2 \mathrm{~s}$ orbital will experience greater nuclear charge (being closer to the nucleus) than the electron(s) in the 3 s orbital.
(ii) 4 d will experience greater nuclear charge than $4 \mathrm{f}$ since $4 \mathrm{~d}$ is closer to the nucleus.
(iii) $3 p$ will experience greater nuclear charge since it is closer to the nucleus than $3 \mathrm{f}$.
Question 64. The unpaired electrons in $\mathrm{Al}$ and $\mathrm{Si}$ are present in $3 \mathrm{p}$ orbital. Which electrons will experience more effective nuclear charge from the nucleus?
Solution: Nuclear charge is defined as the net positive charge experienced by an electron in a multielectron atom. The higher the atomic number, the higher is the nuclear charge. Silicon has 14 protons while aluminium has 13 protons. Hence, silicon has a larger nuclear charge of $(+14)$ than aluminium, which has a nuclear charge of $(+13)$. Thus, the electrons in the $3 \mathrm{p}$ orbital of silicon will experience a more effective nuclear charge than aluminium.
Question 65. Indicate the number of unpaired electrons in:
(a) $\mathrm{P}$
(b) $\mathrm{Si}$
(c) $\mathrm{Cr}$
(d) $\mathrm{Fe}$
(e) $\mathrm{Kr}$
Solution: (a) Phosphorus (P):
We know: Atomic number of $\mathrm{P}=15$
The electronic configuration of $P$ is:
1 s 22 s $22 \mathrm{p} 63 \mathrm{~s} 23 \mathrm{p} 3$
The orbital picture of $\mathrm{P}$ can be represented as:

From the orbital picture, phosphorus has three unpaired electrons.
(b) Silicon (Si):
We know: Atomic number of $\mathrm{Si}=14$
The electronic configuration of Si is:
1s 22 s 22263 s $23 p 2$

From the orbital picture, silicon has two unpaired electrons.
(c) Chromium (Cr):
We know: Atomic number of $\mathrm{Cr}=24$
The electronic configuration of $\mathrm{Cr}$ is:
1 s $22 \mathrm{~s} 22 \mathrm{p} 63 \mathrm{~s} 23 \mathrm{p} 64 \mathrm{~s} 13 \mathrm{~d} 5$
The orbital picture of chromium is:

From the orbital picture, chromium has six unpaired electrons.
(d) Iron (Fe):
We know: Atomic number of $\mathrm{Fe}=26$
The electronic configuration is:
1 s 22 s2 2 p 63 s 23 p 64 s 2336
The orbital picture of chromium is:

From the orbital picture, iron has four unpaired electrons.
(e) Krypton (Kr):
We know: Atomic number of $\mathrm{Kr}=36$
The electronic configuration is:
$1 \mathrm{~s} 22 \mathrm{~s} 22 \mathrm{p} 63 \mathrm{~s} 23 \mathrm{p} 64 \mathrm{~s} 23 \mathrm{~d} 104 \mathrm{p} 6$
The orbital picture of krypton is:
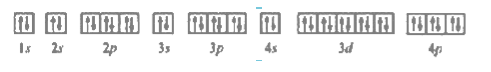
Since all orbitals are fully occupied, there are no unpaired electrons in krypton.
Question 66. (a) How many sub-shells are associated with $\mathrm{n}=4$ ?
(b) How many electrons will be present in the sub-shells having ms value of $-\frac{1}{2}$ for $\mathrm{n}=4$ ?
Solution: (a) Given: $\mathrm{n}=4$
For a given value of ' $\mathrm{n}$ ', ' 'l' can have values from zero to $(\mathrm{n}-1)$.
Therefore, $=0,1,2,3$
Thus, four sub-shells are associated with $\mathrm{n}=4$, which are $\mathrm{s}, \mathrm{p}, \mathrm{d}$ and $\mathrm{f}$.
(b) Given: $\mathrm{n}=4$
Number of orbitals in the $\mathrm{n}$ th shell $=\mathrm{n}^{2}$
For $\mathrm{n}=4$
Number of orbitals $=16$
If each orbital is taken fully, then it will have 1 electron with ms value of.
Therefore, Number of electrons with $\mathrm{m}_{\mathrm{s}}$ value of $(-12)$ is 16 .
Also Read,
Class 11 Chemistry Notes Free PDF Download.
Class 11 Chemistry Book Chapterwise Free PDF Download
Class 11 Chemistry Exemplar Chapterwise Free PDF Download
If you have any Confusion related to NCERT Solutions for Class 11 Chemistry chapter 2 Structure of Atom PDF then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 11 Chemistry by Kota’s top IITian’s Faculties Install the eSaral App
