Hey, do you want to learn about the motion of bodies in contact? If yes. Then you are at the right place.


These two bodies will move with same acceleration = a.
When the force F acts on the body with mass $\mathrm{m}_{1}$
as shown in fig. (1) and (1a) $F=\left(m_{1}+m_{2}\right) a$.
If the force exerted by $\mathrm{m}_{2}$ on $\mathrm{m}_{1}$ is $\mathrm{f}_{1}$ (force of contact)
then for body $\mathrm{m}_{1}$
$\left(F-f_{1}\right)=m_{1} a$
Or
$f_{1}=F-m_{1} a$
$=\left(m_{1}+m_{2}\right) a-m_{1} a=m_{2} a$
or action on $\mathrm{m}_{2}$
$\mathrm{f}_{1}=\mathrm{m}_{2} \cdot \frac{\mathrm{F}}{\mathrm{m}_{1}+\mathrm{m}_{2}}$
When the force F acts on the body with mass $\mathrm{m}_{2}$ as shown in fig. 2 and 2(a)
$\mathrm{F}=\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{a}$

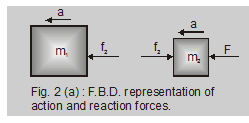
$\mathrm{F}=\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{a}$
for body with mass $\mathrm{m}_{2}$
$\mathrm{F}-\mathrm{f}_{2}=\mathrm{m}_{2} \mathrm{a}$
Or
$\mathrm{f}_{2}=\mathrm{F}-\mathrm{m}_{2} \mathrm{a}$
$=\left(m_{1}+m_{2}\right) a-m_{2} a=m_{1} a$
or action on $\mathrm{m}_{1}$
$\mathrm{f}_{2}=\frac{\mathrm{m}_{1} \mathrm{~F}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}$
Ex. Two blocks of mass m = 2 kg and M = 5 kg are in contact on a frictionless table. A horizontal force F (= 35 N) is applied to m. Find the force of contact between the block, will the force of contact remain same if F is applied to M?

Sol. As the blocks are rigid under the action of a force F, both will move with same acceleration
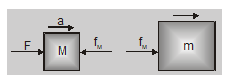
$a=\frac{F}{m+M}=\frac{35}{2+5}=5 \mathrm{~m} / \mathrm{sec}^{2}$
Now as the mass of larger block is M and its acc a,
so, force of contact = action on it
$f_{M}=M a=5 \times 5=25 \mathrm{~N}$
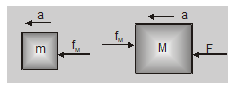
If the force is applied to M then its action on m will be
$\mathrm{f}_{\mathrm{m}}=\mathrm{ma}=2 \times 5=10 \mathrm{~N}$
From this problem, it is clear that acceleration does not depend on the fact that whether the force is applied to m or M, but the force of contact does.
(b) Let us now consider three bodies of masses $m_{1}$, $\mathrm{m}_{2}$ and $\mathrm{m}_{3}$ placed one after another and in contact with each other. Suppose a force F is applied horizontally on mass $\mathrm{m}_{1}$

$\mathrm{F}-\mathrm{f}_{1}=\mathrm{m}_{1} \mathrm{a}$
$f_{1}-f_{2}=m_{2} a$
$\mathrm{f}_{2}=\mathrm{m}_{3} \mathrm{a}$
Here $\mathrm{F}=\left(\mathrm{m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}\right)$ a
$a=\frac{F}{\left(m_{1}+m_{2}+m_{3}\right)}$

$\mathrm{f}_{1}=\frac{\left(\mathrm{m}_{2}+\mathrm{m}_{3}\right) \mathrm{F}}{\left(\mathrm{m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}\right)}$ (action on both $\mathrm{m}_{2}$ and $\left.\mathrm{m}_{3}\right)$
And
$f_{2}=\frac{m_{3} F}{\left(m_{1}+m_{2}+m_{3}\right)}$
(action on $\mathrm{m}_{3}$ alone)
when the force F is applied on $m_{3}$, then
$\mathrm{f}_{1}=\frac{\mathrm{m}_{1} \mathrm{~F}}{\left(\mathrm{~m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}\right)}$ (action on $\mathrm{m}_{1}$ alone)
and $f_{2}=\frac{\left(m_{1}+m_{2}\right) F}{\left(m_{1}+m_{2}+m_{3}\right)}$
(action on $\mathrm{m}_{1}$ and $\mathrm{m}_{2}$ )
So, that's all from this blog. I hope you get the idea about the Motion of bodies in contact. If you enjoyed this explanation then please share it with your friends.
Also, read
Application of impulse
To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
The motion of bodies in contact
(a) When two bodies of masses $\mathrm{m}_{1}$ and $\mathrm{m}_{2}$ are kept on the frictionless surface and a force F is applied on one body, then the force with which one body presses the other at the point of contact is called Force of Contact.

These two bodies will move with same acceleration = a.
When the force F acts on the body with mass $\mathrm{m}_{1}$
as shown in fig. (1) and (1a) $F=\left(m_{1}+m_{2}\right) a$.
If the force exerted by $\mathrm{m}_{2}$ on $\mathrm{m}_{1}$ is $\mathrm{f}_{1}$ (force of contact)
then for body $\mathrm{m}_{1}$
$\left(F-f_{1}\right)=m_{1} a$
Or
$f_{1}=F-m_{1} a$
$=\left(m_{1}+m_{2}\right) a-m_{1} a=m_{2} a$
or action on $\mathrm{m}_{2}$
$\mathrm{f}_{1}=\mathrm{m}_{2} \cdot \frac{\mathrm{F}}{\mathrm{m}_{1}+\mathrm{m}_{2}}$
When the force F acts on the body with mass $\mathrm{m}_{2}$ as shown in fig. 2 and 2(a)
$\mathrm{F}=\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{a}$


$\mathrm{F}=\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{a}$
for body with mass $\mathrm{m}_{2}$
$\mathrm{F}-\mathrm{f}_{2}=\mathrm{m}_{2} \mathrm{a}$
Or
$\mathrm{f}_{2}=\mathrm{F}-\mathrm{m}_{2} \mathrm{a}$
$=\left(m_{1}+m_{2}\right) a-m_{2} a=m_{1} a$
or action on $\mathrm{m}_{1}$
$\mathrm{f}_{2}=\frac{\mathrm{m}_{1} \mathrm{~F}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}$
Ex. Two blocks of mass m = 2 kg and M = 5 kg are in contact on a frictionless table. A horizontal force F (= 35 N) is applied to m. Find the force of contact between the block, will the force of contact remain same if F is applied to M?

Sol. As the blocks are rigid under the action of a force F, both will move with same acceleration

$a=\frac{F}{m+M}=\frac{35}{2+5}=5 \mathrm{~m} / \mathrm{sec}^{2}$
Now as the mass of larger block is M and its acc a,
so, force of contact = action on it
$f_{M}=M a=5 \times 5=25 \mathrm{~N}$

If the force is applied to M then its action on m will be
$\mathrm{f}_{\mathrm{m}}=\mathrm{ma}=2 \times 5=10 \mathrm{~N}$
From this problem, it is clear that acceleration does not depend on the fact that whether the force is applied to m or M, but the force of contact does.
(b) Let us now consider three bodies of masses $m_{1}$, $\mathrm{m}_{2}$ and $\mathrm{m}_{3}$ placed one after another and in contact with each other. Suppose a force F is applied horizontally on mass $\mathrm{m}_{1}$

$\mathrm{F}-\mathrm{f}_{1}=\mathrm{m}_{1} \mathrm{a}$
$f_{1}-f_{2}=m_{2} a$
$\mathrm{f}_{2}=\mathrm{m}_{3} \mathrm{a}$
Here $\mathrm{F}=\left(\mathrm{m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}\right)$ a
$a=\frac{F}{\left(m_{1}+m_{2}+m_{3}\right)}$

$\mathrm{f}_{1}=\frac{\left(\mathrm{m}_{2}+\mathrm{m}_{3}\right) \mathrm{F}}{\left(\mathrm{m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}\right)}$ (action on both $\mathrm{m}_{2}$ and $\left.\mathrm{m}_{3}\right)$
And
$f_{2}=\frac{m_{3} F}{\left(m_{1}+m_{2}+m_{3}\right)}$
(action on $\mathrm{m}_{3}$ alone)
when the force F is applied on $m_{3}$, then
$\mathrm{f}_{1}=\frac{\mathrm{m}_{1} \mathrm{~F}}{\left(\mathrm{~m}_{1}+\mathrm{m}_{2}+\mathrm{m}_{3}\right)}$ (action on $\mathrm{m}_{1}$ alone)
and $f_{2}=\frac{\left(m_{1}+m_{2}\right) F}{\left(m_{1}+m_{2}+m_{3}\right)}$
(action on $\mathrm{m}_{1}$ and $\mathrm{m}_{2}$ )
So, that's all from this blog. I hope you get the idea about the Motion of bodies in contact. If you enjoyed this explanation then please share it with your friends.
Also, read
Application of impulse
To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
