JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. Let $\mathrm{f}: \mathrm{R} \rightarrow \mathrm{R}$ be a positive increasing function with $\lim _{x \rightarrow \infty} \frac{\mathrm{f}(3 \mathrm{x})}{\mathrm{f}(\mathrm{x})}=1 .$ Then $\lim _{\mathrm{x} \rightarrow \infty} \frac{\mathrm{f}(2 \mathrm{x})}{\mathrm{f}(\mathrm{x})}=$
(1) 1
(2) $\frac{2}{3}$
(3) $\frac{3}{2}$
(4) 3
[AIEEE-2010]
Ans. (1)
$\mathrm{f}(\mathrm{x})$ is a positive increasing function
$\Rightarrow 0<\mathrm{f}(\mathrm{x})<\mathrm{f}(2 \mathrm{x})<\mathrm{f}(3 \mathrm{x})$
$\Rightarrow 0<1<\frac{\mathrm{f}(2 \mathrm{x})}{\mathrm{f}(\mathrm{x})}<\frac{\mathrm{f}(3 \mathrm{x})}{\mathrm{f}(\mathrm{x})}$
$\Rightarrow \lim _{x \rightarrow \infty} 1 \leq \lim _{x \rightarrow \infty} \frac{f(2 x)}{f(x)} \leq \lim _{x \rightarrow \infty} \frac{f(3 x)}{f(x)}$
By sandwich theorem.
$\Rightarrow \lim _{x \rightarrow \infty} \frac{f(2 x)}{f(x)}=1$
Q. $\lim _{x \rightarrow 2}\left(\frac{\sqrt{1-\cos \{2(x-2)\}}}{x-2}\right)$
(1) equals $-\sqrt{2}$
(2) equals $\frac{1}{\sqrt{2}}$
(3) does not exist
(4) equals $\sqrt{2}$
[AIEEE-2011]
Ans. (3)
$\lim _{x \rightarrow 2} \frac{\sqrt{1-\cos 2(x-2)}}{(x-2)}=\lim _{x \rightarrow 2} \frac{\sqrt{2 \sin ^{2}(x-2)}}{(x-2)}$
$=\lim _{x \rightarrow 2} \frac{\sqrt{2}|\sin (x-2)|}{(x-2)}$
$\mathrm{RHL}$ at $\mathrm{x}=2, \lim _{\mathrm{h} \rightarrow 0} \frac{\sqrt{2}|\sin (2+\mathrm{h}-2)|}{(2+\mathrm{h})-2}=\lim _{\mathrm{h} \rightarrow 0} \frac{\sqrt{2}|\sinh |}{\mathrm{h}}$
$=\lim _{h \rightarrow 0} \frac{\sqrt{2} \sinh }{-h}=-\sqrt{2}$
LHL at $\mathrm{x}=2, \lim _{\mathrm{h} \rightarrow 0} \frac{\sqrt{2}|\sin (2-\mathrm{h}-2)|}{(2-\mathrm{h})-2}$
$=\lim _{h \rightarrow 0} \frac{\sqrt{2}|\sin (-h)|}{-h}=\lim _{h \rightarrow 0} \frac{\sqrt{2} \sinh }{-h}=-\sqrt{2}$
$\because \mathrm{LHL} \neq \mathrm{RHL}$
Hence, limit does not exist.
Q. Let $f: \mathrm{R} \rightarrow[0, \infty)$ be such that $\lim _{x \rightarrow 5} f(x)$ exists and $\lim _{x \rightarrow 5} \frac{(f(x))^{2}-9}{\sqrt{|x-5|}}=0 .$ Then $\lim _{x \rightarrow 5} \operatorname{Lim}_{x \rightarrow 5}(x)$ equal –
(1) 3 (2) 0 (3) 1 (4) 2
[AIEEE-2011]
Ans. (1)
$\lim _{x \rightarrow 5} \frac{(f(x))^{2}-9}{\sqrt{|x-5|}}=0$
$\therefore \quad$ Question must be in $\frac{0}{0}$ form
$\therefore \quad(f(5))^{2}-9=0$
$\Rightarrow \quad f(5)=3$
Q. $\lim _{x \rightarrow 0} \frac{\sin \left(\pi \cos ^{2} x\right)}{x^{2}}$ is equal to:
(1) $\frac{\pi}{2}$
(2) 1
$(3)-\pi$
(4)$\pi$
[JEE Mains Offline-2014]
Ans. (4)
$\lim _{x \rightarrow 0} \frac{\sin \left(\pi \cos ^{2} x\right)}{x^{2}}$
$\Rightarrow \lim _{x \rightarrow 0} \frac{\sin \left(\pi-\pi \sin ^{2} x\right)}{x^{2}}$
$\Rightarrow \lim _{x \rightarrow 0} \frac{\sin \left(\pi \sin ^{2} x\right)}{\pi \sin ^{2} x} \times \pi \frac{\sin ^{2} x}{x^{2}}$
$\Rightarrow \lim _{x \rightarrow 0} \frac{\sin \left(\pi \sin ^{2} x\right)}{\pi \sin ^{2} x} \times \pi \times \lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^{2}$
$\Rightarrow 1 \times \pi \times 1$
$=\pi$
Q. If $\lim _{x \rightarrow 2} \frac{\tan (x-2)\left\{x^{2}+(k-2) x-2 k\right\}}{x^{2}-4 x+4}=5$ then $k$ is equal to
(1) 3 (2) 1 (3) 0 (4) 2
[JEE Mains Online-2014]
Ans. (1)
If $\lim _{x \rightarrow 2} \frac{\tan (x-2)\left[x^{2}+k x-2 k-2 x\right]}{(x-2)^{2}}=5$
$\lim _{x \rightarrow 2}\left(\frac{\tan (x-2)}{(x-2)}\right) \frac{(x+k)(x-2)}{(x-2)}=5$
1. (2 + k) = 5
K = 3
Q. Let $\mathrm{p}=\lim _{x \rightarrow 0+}\left(1+\tan ^{2} \sqrt{\mathrm{x}}\right)^{\frac{1}{2 \mathrm{x}}}$ then log $\mathrm{p}$ is equal to :-
(1) $\frac{1}{4}$
(2) 2
(3) 1
(4) $\frac{1}{2}$
[JEE Mains -2016]
Ans. (4)
$\mathrm{p}=\mathrm{e}^{\mathrm{x} \rightarrow 0^{\frac{1}{2}}\left(\frac{\tan \sqrt{x}}{\sqrt{x}}\right)^{2}}=\sqrt{\mathrm{e}}$
$\log \mathrm{p}=\frac{1}{2}$
Q. $\lim _{n \rightarrow \infty}\left(\frac{(n+1)(n+2) \ldots .3 n}{n^{2 n}}\right)^{1 / n}$ is equal to :-
(1) $3 \log 3-2$
(2) $\frac{18}{\mathrm{e}^{4}}$b
(3) $\frac{27}{\mathrm{e}^{2}}$
(4) $\frac{9}{\mathrm{e}^{2}}$
[JEE Mains 2016]
Ans. (3)
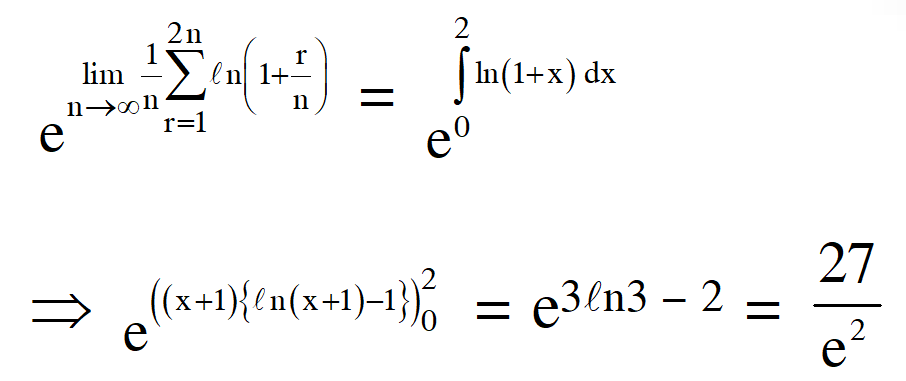
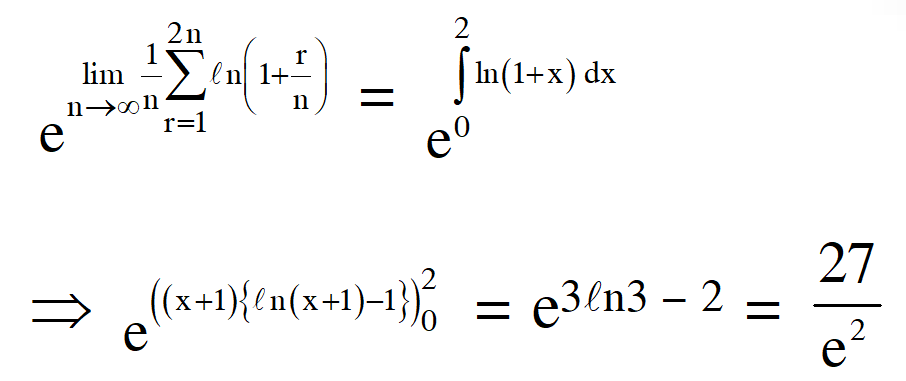
Q. $\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cot x-\cos x}{(\pi-2 x)^{3}}$ equals :-
(1) $\frac{1}{4}$
(2) $\frac{1}{24}$
(3) $\frac{1}{16}$
(4) $\frac{1}{8}$
[JEE Mains -2017]
Ans. (3)
$\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cot x(1-\sin x)}{-8\left(x-\frac{\pi}{2}\right)^{3}}$
$=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan \left(\frac{\pi}{2}-x\right)}{8\left(\frac{\pi}{2}-x\right)} \frac{\left(1-\cos \left(\frac{\pi}{2}-x\right)\right)}{\left(\frac{\pi}{2}-x\right)^{2}}$
$=\frac{1}{8} \cdot 1 \cdot \frac{1}{2}=\frac{1}{16}$
Q. For each $\mathrm{t} \in \mathrm{R},$ let $[\mathrm{t}]$ be the greatest integer less than or equal to t. Then
$\lim _{\mathrm{x} \rightarrow 0+} \mathrm{x}\left(\left[\frac{1}{\mathrm{x}}\right]+\left[\frac{2}{\mathrm{x}}\right]+\ldots \ldots+\left[\frac{15}{\mathrm{x}}\right]\right)$\
(1) is equal to 15.
(2) is equal to 120.
(3) does not exist (in R).
(4) is equal to 0.
[JEE Mains -2018]
Ans. (2)


Q. $\lim _{x \rightarrow 0} \frac{(27+x)^{1 / 3}-3}{9-(27+x)^{2 / 3}}$ equals :
$(1)-\frac{1}{3}$
(2) $\frac{1}{6}$
$(3)-\frac{1}{6}$
(4) $\frac{1}{3}$
[JEE Mains -2018]
Ans. (3)
Q. $\lim _{x \rightarrow 0} \frac{x \tan 2 x-2 x \tan x}{(1-\cos 2 x)^{2}}$ equals :-
$(1)-\frac{1}{2}$
(2) $\frac{1}{4}$
(3) $\frac{1}{2}$
(4) 1
[JEE Mains -2018]
Ans. (3)
Comments
Abheeshna Dey
Nov. 15, 2024, 6:31 p.m.
More varieties of questions from last 10 years of JEE Mains&Advanced should be provided.
Ali
Feb. 7, 2024, 12:34 p.m.
Wow, fantastic blog structure! How long have you ever
been blogging for? you made blogging look easy. The overall
look of your web site is excellent, let alone the content material!
You can see similar: Novoluxe.top and here Novoluxe.top
international pharmacy
Oct. 18, 2023, 6:35 a.m.
Do you have a spam issue on this site; I also am a blogger, and I was wondering your situation; many of us have created some nice methods and we are looking to trade solutions with other folks, why not shoot me an e-mail if interested.
Rohith
Dec. 8, 2020, 11:51 a.m.
Hey! Thanks for the questions.But there are no solutions for some questions please look into those question kindly update answers it would be helpful
Thank you.
Vivek
Aug. 16, 2020, 9:06 p.m.
For anyone having problems seeing the questions, right-click on the equation part, click "Show Math as", then click "MathML code". Copy all the text in the new window that opens with Ctrl+A. Now open a new tab and type in this URL: http://www.wiris.com/editor/demo/en/developers . And paste whatever you copied! Woila! Thank me later!
