JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics dwill help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. Three distinct points A, B and C are given in the 2–dimensional coordinate plane such that the ratio of the distance of any one of them from the point (1, 0) to the distance from the point (–1, 0) is equal to $\frac{1}{3}$. Then the circumcentre of the triangle ABC is at the point :-
(1) $\left(\frac{5}{2}, 0\right)$
( 2)$\left(\frac{5}{3}, 0\right)$
(3) (0, 0)
( 4)$\left(\frac{5}{4}, 0\right)$
[AIEEE-2009]
Ans. (4)
Let $A, B, C$ are represented by the point $(x, y)$
$\frac{\sqrt{(x-1)^{2}+y^{2}}}{\sqrt{(x+1)^{2}+y^{2}}}=\frac{1}{2}$
$8 x^{2}+8 y^{2}-20 x+8=0$
Which is the circle which passes through the points $A, B, C$ then circumcentre will be the centre
of the circle $\left(\frac{5}{4}, 0\right)$
Q. If $P$ and $Q$ are the points of intersection of the circles $x^{2}+y^{2}+3 x+7 y+2 p-5=0$ and $x^{2}+y^{2}+2 x+2 y-p^{2}=0,$ then there is a circle passing through $P, Q$ and $(1,1)$ is possible for : $-$
(1) All except two values of p
(2) Exactly one value of p
(3) All values of p
(4) All except one value of p
[AIEEE-2009]
Ans. (4)
Equation of line $\mathrm{PQ}$
$\mathrm{x}+5 \mathrm{y}+2 \mathrm{p}-5+\mathrm{p}^{2}=0$
$\mathrm{P}, \mathrm{Q}$ and $(1,1)$
will not lie on a circle of $(1,1)$
Lies on the line $\mathrm{x}+5 \mathrm{y}+\mathrm{p}^{2}+2 \mathrm{p}-5=0$
Q. For a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. A false statement among the following is :-
(1) There is a regular polygon with $\frac{\mathrm{r}}{\mathrm{R}}=\frac{1}{2}$
(2) There is a regular polygon with $\frac{r}{R}=\frac{1}{\sqrt{2}}$
(3) There is a regular polygon with $\frac{\mathrm{r}}{\mathrm{R}}=\frac{2}{3}$b
(4) There is a regular polygon with $\frac{\mathrm{r}}{\mathrm{R}}=\frac{\sqrt{3}}{2}$
[AIEEE-2010]
Ans. (3)
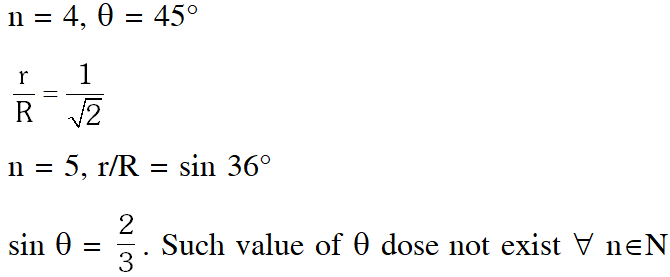
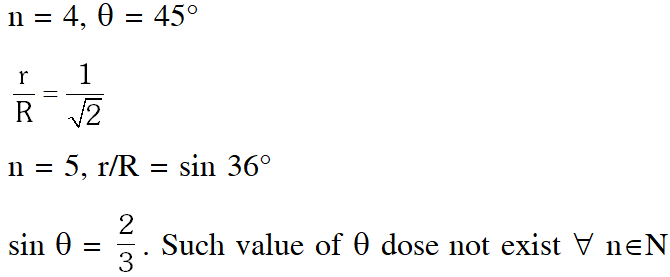
Q. The circle $\mathrm{x}^{2}+\mathrm{y}^{2}=4 \mathrm{x}+8 \mathrm{y}+5$ intersects the line $3 \mathrm{x}-4 \mathrm{y}=\mathrm{m}$ at two distinct points if :-
(1) – 85 < m < – 35 (2) – 35 < m < 15 (3) 15 < m < 65 (4) 35 < m < 85
[AIEEE-2010]
Ans. (2)
Q. The two circles $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{ax}$ and $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{c}^{2}(\mathrm{c}>0)$ touch each other if :-
(1) $\mathrm{a}=2 \mathrm{c}$
(2) $|\mathrm{a}|=2 \mathrm{c}$
(3) $2|\mathrm{a}|=\mathrm{c}$
(4) $|\mathrm{a}|=\mathrm{c}$
[AIEEE-2011]
Ans. (4)
Q. The equation of the circle passing through the points (1, 0) and (0, 1) and having the smallest radius is –
(1) $x^{2}+y^{2}+x+y-2=0$
(2) $x^{2}+y^{2}-2 x-2 y+1=0$
(3) $x^{2}+y^{2}-x-y=0$
(4) $x^{2}+y^{2}+2 x+2 y-7=0$
[AIEEE-2011]
Ans. (3)
(1, 0) and (0, 1) will be ends of diameter
So equation of circle
(x- 1) ( $\mathrm{x}-0)+(\mathrm{y}-0)(\mathrm{y}-1)$
$\mathrm{x}^{2}+\mathrm{y}^{2}-\mathrm{x}-\mathrm{y}=0$
Q. The length of the diameter of the circle which touches the x-axis at the point (1, 0) and passes through the point (2, 3) is :
(1) 5/3 (2) 10/3 (3) 3/5 (4) 6/5
[AIEEE-2012]
Ans. (2)
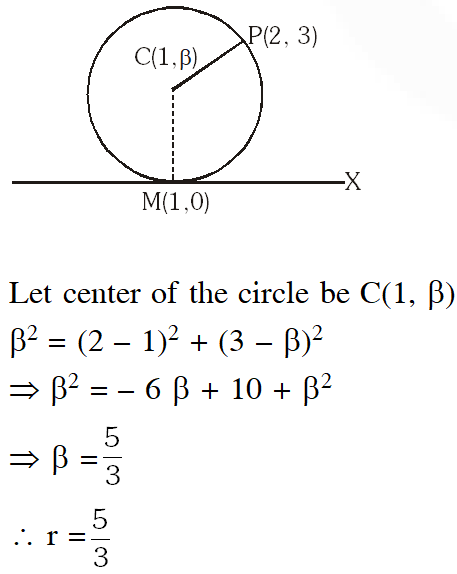diameter $=\frac{10}{3}$
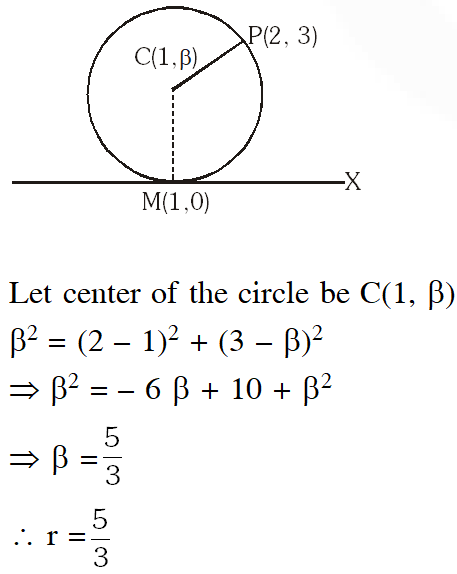diameter $=\frac{10}{3}$
Q. The circle passing through (1, – 2) and touching the axis of x at (3, 0) also passes through the point :
(1) (–5, 2) (2) (2, –5) (3) (5, –2) (4) (–2, 5)
[JEE (Main)-2013]
Ans. (3)
Let equation of circle be $(\mathrm{x}-3)^{2}+(\mathrm{y}+\mathrm{r})^{2}=\mathrm{r}^{2} \because$ it passes through $(1,-2)$
$\Rightarrow \mathrm{r}=2$
$\Rightarrow \quad$ circle is $(\mathrm{x}-3)^{2}+(\mathrm{y}+2)^{2}=4$
$\Rightarrow \quad(5,-2)$
Aliter :
$(\mathrm{x}-3)^{2}+\mathrm{y}^{2}+\lambda \mathrm{y}=0 \quad \ldots .(1)$
Putting $(1,-2)$ in ( 1)
$\Rightarrow \lambda=4$
Required circle is
$\mathrm{x}^{2}+\mathrm{y}^{2}-6 \mathrm{x}+4 \mathrm{y}+9=0$
point $(5,-2)$ satisfies the equation the equation
Q. If a circle $C$ passing through $(4,0)$ touches the circle $x^{2}+y^{2}+4 x-6 y-12=0$ externally at a point $(1,-1),$ then the radius of the circle $C$ is :-
(1) $\sqrt{57}$
(2) $2 \sqrt{5}$
(3) 4
(4) 5
[JEE (Main)-2013]
Ans. (4)
Equation of family of circles is
$(\mathrm{x}-1)^{2}+(\mathrm{y}+1)^{2}+\lambda\left(\mathrm{x}^{2}+\mathrm{y}^{2}+4 \mathrm{x}-6 \mathrm{y}-12\right)=0$
Now it passes of through $(4,0)$ we get
$\Rightarrow 9+1+\lambda(16+16-12)=0 \Rightarrow \lambda=-\frac{10}{20}=-\frac{1}{2}$
Required equation of circle is $\mathrm{x}^{2}+\mathrm{y}^{2}-2 \mathrm{x}+2 \mathrm{y}+2-\frac{1}{2}\left(\mathrm{x}^{2}+\mathrm{y}^{2}+4 \mathrm{x}-6 \mathrm{y}-12\right)=0$
$\Rightarrow \mathrm{x}^{2}+\mathrm{y}^{2}-8 \mathrm{x}+10 \mathrm{y}+16=0$
radius $=\sqrt{16+25-16}=5$
Q. If the circle $x^{2}+y^{2}-6 x-8 y+\left(25-a^{2}\right)=0$ touches the axis of $x,$ then a equals :-
$(1) \pm 4$
$(2) \pm 3$
(3) 0
$(4) \pm 2$
[JEE-Main (on line)-2013]
Ans. (3,4)
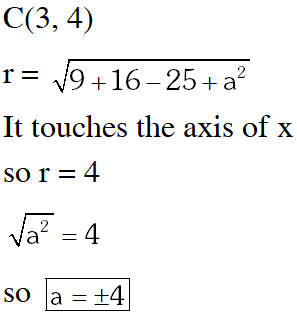
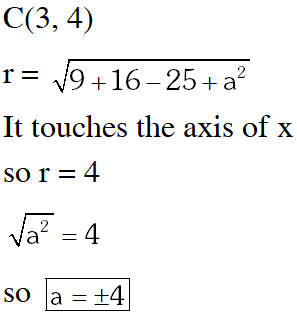
Q. Statement I : The only circle having radius $\sqrt{10}$ and a diameter along line $2 \mathrm{x}+\mathrm{y}=5$ is $\mathrm{x}^{2}+\mathrm{y}^{2}-6 \mathrm{x}+2 \mathrm{y}=0$
Statement $\mathbf{I I}: 2 \mathbf{x}+\mathrm{y}=5$ is a normal to the circle $\mathrm{x}^{2}+\mathrm{y}^{2}-6 \mathrm{x}+2 \mathrm{y}=0$.
[JEE-Main (on line)-2013]
(1) Statement I is false, Statement II is true
(2) Statement I is true ; Statement II is false.
(3) Statement I is true, Statement II is true, Statement II is not a correct explanation for
Statement I.
(4) Statement I is true : Statement II is true ; Statement II is a correct explanation for Statement I.
[JEE-Main (on line)-2013]
Ans. (1)
Normal passes through centre of circle but there can be more then one circle.
Q. Let C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to :
(1) $\frac{\sqrt{3}}{\sqrt{2}}$
( 2)$\frac{\sqrt{3}}{2}$
(3) $\frac{1}{2}$
(4) $\frac{1}{4}$
[JEE(Main)-2014]
Ans. (4)
$\mathrm{C}_{1} \mathrm{C}_{2}=\mathrm{r}_{1}+\mathrm{r}_{2}$
$\sqrt{1+(1-\mathrm{y})^{2}}=1+\mathrm{y}$
$\therefore \mathrm{y}=\frac{1}{4}$
$\therefore \mathrm{radius}=\frac{1}{4}$
Q. The number of common tangents to the circle $x^{2}+y^{2}-4 x-6 y-12=0$ and $x^{2}+y^{2}+6 x$ $+18 y+26=0,$ is :
(1) 3 (2) 4 (3) 1 (4) 2
[JEE(Main)-2015]
Ans. (1)
distance between centres $\left(\mathrm{c}_{1} \mathrm{c}_{2}\right)=13$
$\mathrm{r}_{1}=\sqrt{4+9+12}=5 \& \mathrm{r}_{2}=\sqrt{9+81-26}=8$
$\mathrm{c}_{1} \mathrm{c}_{2}=\mathrm{r}_{1}+\mathrm{r}_{2}$ is a case of external touching (as shown in above figure), so three common tangentscan be drawn.
distance between centres $\left(\mathrm{c}_{1} \mathrm{c}_{2}\right)=13$
$\mathrm{r}_{1}=\sqrt{4+9+12}=5 \& \mathrm{r}_{2}=\sqrt{9+81-26}=8$
$\mathrm{c}_{1} \mathrm{c}_{2}=\mathrm{r}_{1}+\mathrm{r}_{2}$ is a case of external touching (as shown in above figure), so three common tangentscan be drawn.
Q. If one of the diameters of the circle, given by the euqation, $x^{2}+y^{2}-4 x+6 y-12=0,$ is
a chord of a circle $S,$ whose centre is at $(-3,2),$ then the radius of $S$ is : $-$
(1) 10
(2) $5 \sqrt{2}$
(3) $5 \sqrt{3}$
(4) 5
[JEE(Main)-2016]
Ans. (3)
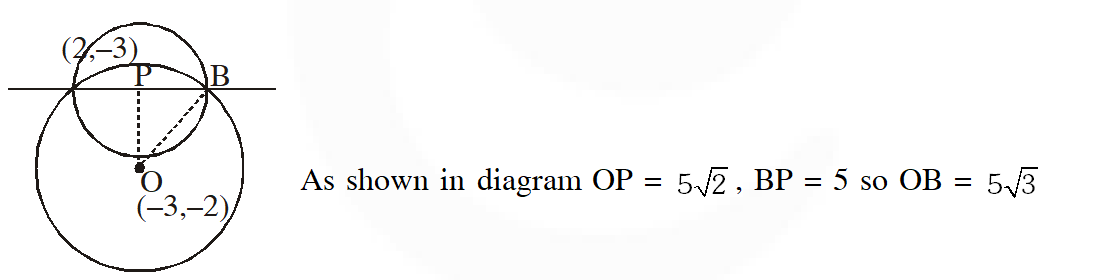
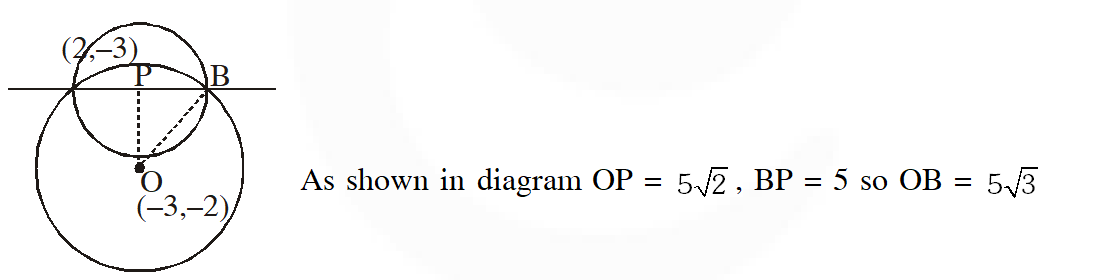
Q. The centres of those circles which touch the circle, $x^{2}+y^{2}-8 x-8 y-4=0,$ externally
and also touch the $x$ -axis, lie on :-
(1) A parabola
(2) A circle
(3) An ellipse which is not a circle
(4) A hyperbola
[JEE(Main)-2016]
Ans. (1)
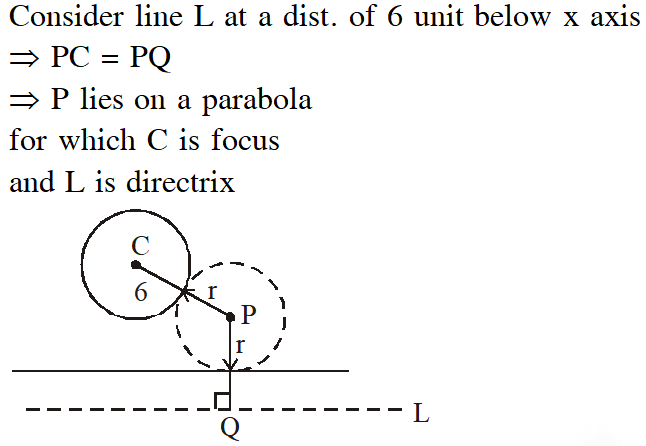
Q. If the tangent at $(1,7)$ to the curve $x^{2}=y-6$ touches the circle $x^{2}+y^{2}+16 x+12 y+c=0$ then the value of $c$ is :
(1) 185 (2) 85 (3) 95 (4) 195
[JEE(Main)-2018]
Ans. (3)
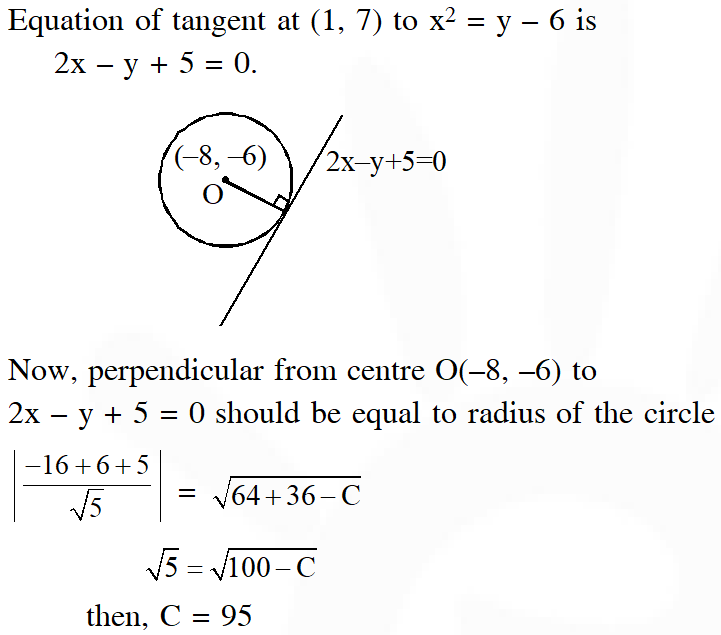
Comments
Abhinesh
Dec. 30, 2020, 10:57 a.m.
These are easy question but very helpful thankyou esaral please upload advance recent questions sir
Uday Krishna
Aug. 3, 2020, 5:21 p.m.
These questions are good but you need to update to upload recent years also
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.